 Sideway
BICK BLOG from Sideway
Sideway
BICK BLOG from Sideway
|
Link:http://output.to/sideway/default.asp?qno=110900018 Direction Slope of Tangent LineSecant line is the straight line joining the function y=ƒ(x) at x and x+Δx. Slope is the rate of change of a straight line. Therefore the rate of change of the secant line is equal to the slope of the secant line. Since the tangent line at x can be approximated by the secant line when applying limit Δx to zero, the derivative can be considered as the slope of tangent line at x. 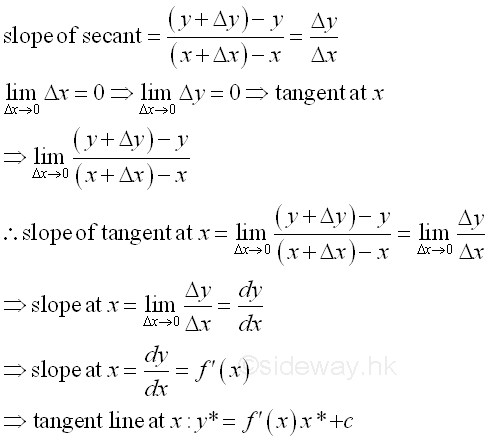
Direction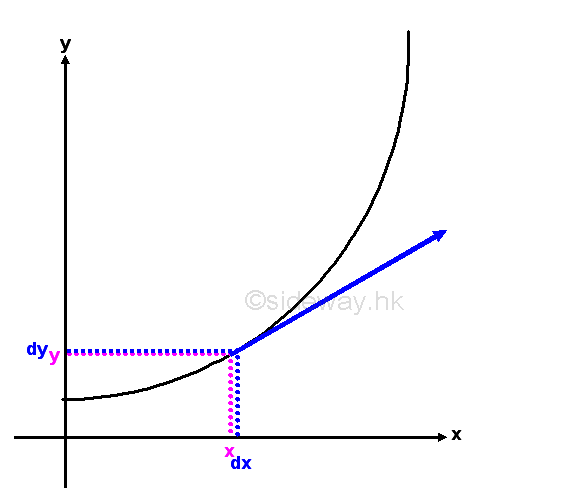
The motion of an object usually has both magnitude and direction. In general, the velocity of motion is always tangent to the path of the object motion. Therefore the direction of motion at position x in a circular or curvilinear motion is alway parallel to the tangent line at position x. Circular Motion Problem
For a circular motion with uniform angular speed ω, the relationship between the displacement in x and the displacement in y can be expressed as a function:
The derivative of function with respect to x is 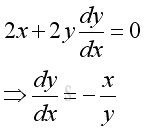
Therefore the derivative of function y with respect to x is a function of x and y. The minus sign means a negative slope. And express the derivative of function with respect to x in term of x, imply: 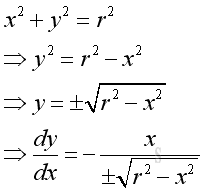
The plus and minus sign of displacement y represent the upper half circle and the lower half circle of the circular motion. Let the radius r of the circular motion be 5. The derivative, slope of the direction of the object motion is:
Graphically: 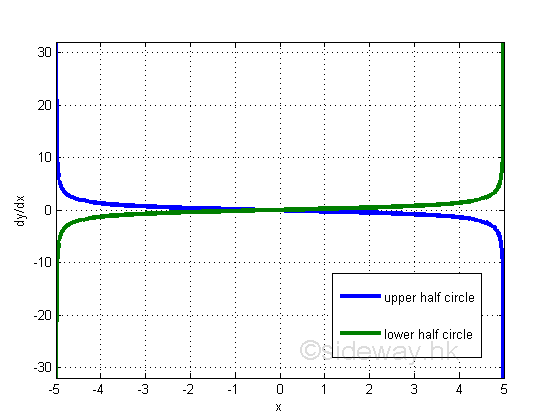
Projectile Problem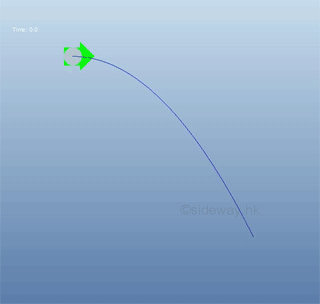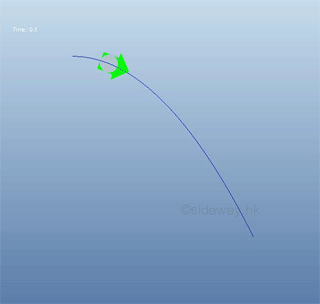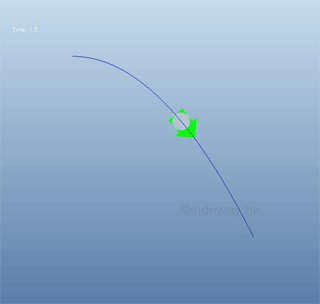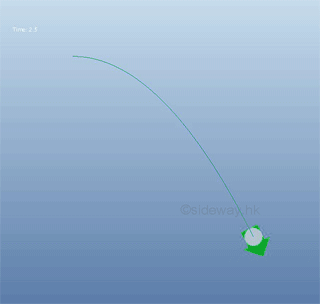
For parabolic motion of a projectile with uniform horizontal speed v, the relationship between the displacement in x and the displacement in y can be expressed as a function:
The derivative of function with respect to x is 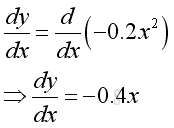
The derivative of function y with respect to x is a function of x only. The minus sign means a negative slope. The derivative, slope of the direction of the object motion is:
Graphically: 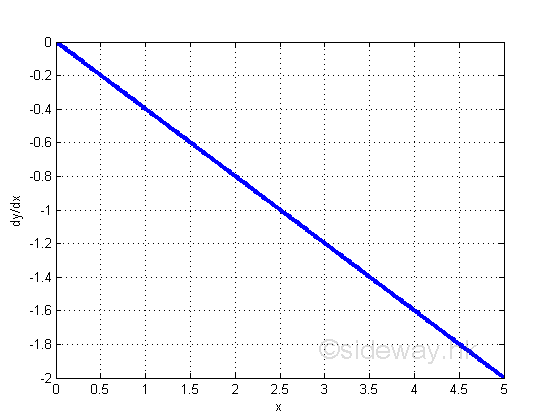
|
Sideway BICK Blog 24/09 |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
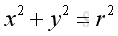 and
and
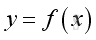
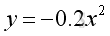 and
and

