 Sideway
BICK BLOG from Sideway
Sideway
BICK BLOG from Sideway
|
Link:http://output.to/sideway/default.asp?qno=110900027 Shape of Curve Slope of Tangent LineBoth the first derivative and second derivative of a function can provide the gradient information about steepness of the graph of the function. The common applications of slope of tangent are curve sketching and relative extreme value finding. Curve SketchingBefore sketching the curve of the function, some important points should be found first. The first type of points are critical points at which the derivative equals zero or does not exist. The second type of points are the stationary or turning points, they can be the position of points of inflexion, points of local minima, and points of local maxima. Another types of points are the y-intercept and x-intercepts. After finding these importants positions, the next step is to carry out a gradient or slope analysis for the basic sketching of the curve. Finally the curve can be drafted according to the acquired information. Curve Sketching ProblemThe shape of the curve of a function y=x3-7x2+14x-8 is:
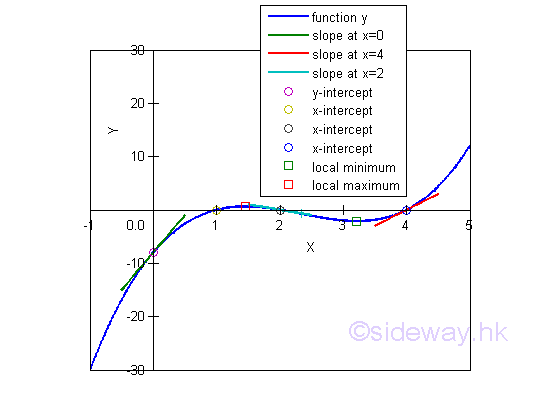
Relative Extreme ValueOptimization is one of the most important processes in industry. When interpreting the design criteria as constraints, a design problem can then be modelled, analyzed and evaluated using a mathematical model. In general, optimization is the process of finding maximum or minimum values of a task. When expressing requirements as a function, the optimization processes becomes a finding maximum or minimum value problem. Relative Maximum ProblemGiven a sheet of metal with size 4x6 to build a retangular container with the width equal half of length. The maximum volume is: In order to make the retangular container, four square corners of lenght x are cut away. 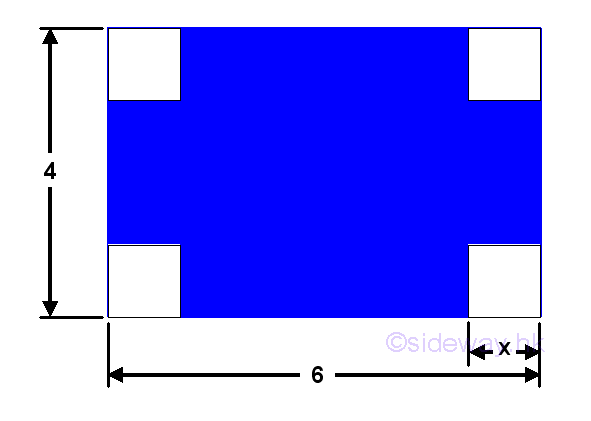
According to the criteria, the value of x is limited in the domain [0,2]. Let x be the height, then width equals to 4-2x and length equals to 6-2x. The problem can be modelled as: 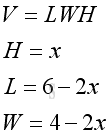
The volume of the retangular container is: 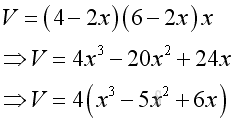
To determine the maximum volume of a rectangular container from the metal sheet, the volume can be evaluated with respect to x, that is to analyze by means of differentiation. Take the first derivative of the volume function with respect to x equals to zero to determine the stationary points: 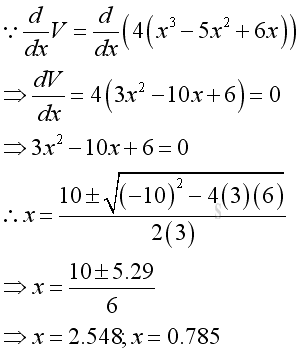
Since x can not be equal to 2.548 because of larger than 2, x can be 0.785 only. Find the value of the second derivative at the stationary point, 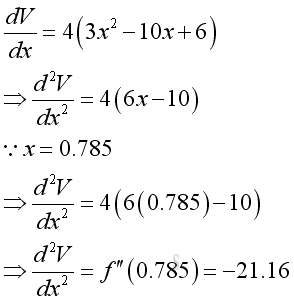
Since the second derivative less than zero, the position of x=0.785 is the largest volume. That is 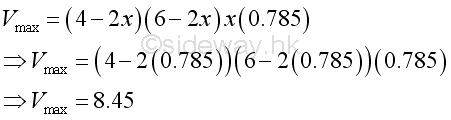
Graphically, 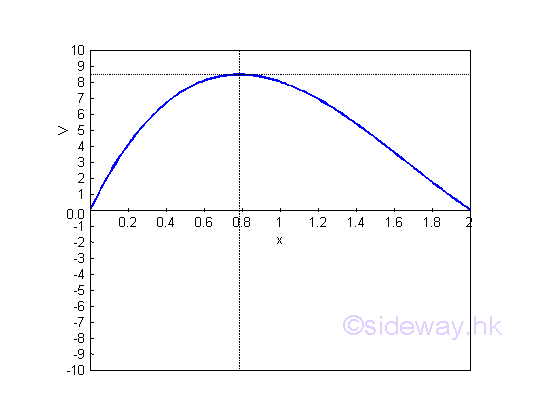
Relative Minimum ProblemGiven a sheet metal to build a retangular container with height 0.785 and volume 8.45. The minimum material used is. In order to make the retangular container, four square corners of lenght x are cut away. 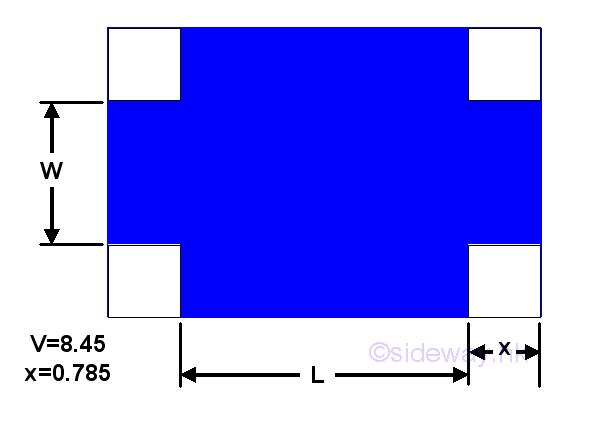
According to the criteria, given volume is 8.45 and the height of the container is 0.785. Let W be the width of the rectangular container, L be the length of rectangular container. The problem can be modelled as:. 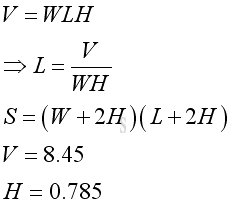
Let x be the width W of the rectangular container. The surface area of the metal sheet for the retangular container in terms of x is: 
Therefore, the minimum dimension of the metal sheet is transformed to a function of the width of the rectangular container. The minimum dimension of the metal sheet can therefore can be evaluated with respect to x, the width of the rectangular container that is to analyze by means of differentiation. Take the first derivative of the surface area function with respect to x equals to zero to determine the stationary points: 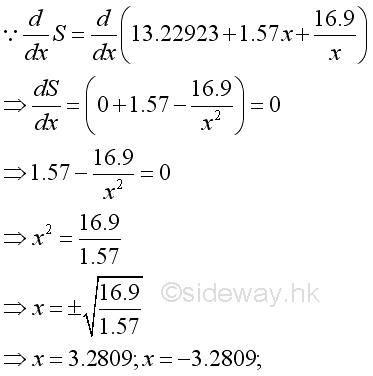
Since x can not be equal to -3.2809, a negative number, x can be 3.2809 only. Find the value of the second derivative at the stationary point, 
Since the second derivative greater than zero, the position of x=3.2809 is the minimum surface area of the metal sheet. That is 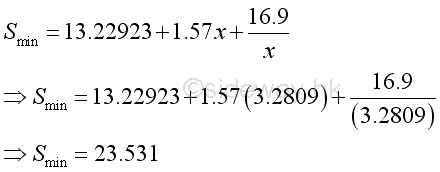
Graphically, 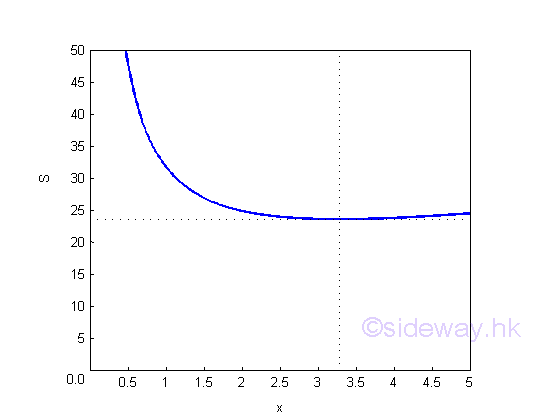
The dimension of the metal sheet is, 
The minimum dimension of the metal sheet is a square metal sheet of dimension, 4.8509x4.8509=23.531. The material usage for building the rectangular container is less than the 4x6 metal sheet. The maximum value problem of the first example is the optimization of the usage of available material for the application of designing a rectangular container, while the minumum value porblem of this example is the optimization of the material usage in a required rectangular container design. Link:http://output.to/sideway/default.asp?qno=110900026 Shape of Curve Slope of Tangent LineWhen interpreting the derivative as the slope of tangent line at x, the derivative of function y can provide the gradient information about steepness of the graph of the function. Shape of CurveFor some simple functions in domain [0,5], the function can be always increasing, remaining constant, or always decreasing. 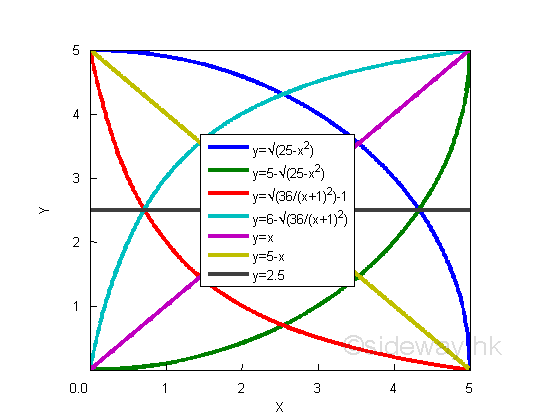
MonotonicityFor a monotonically increasing function y, the value of ratio Δy over Δx is always positive, therefore the value of derivaive is also always positive. The derivative of the straight line y=f(x)=x is equal to 1. The derivatives of curves in domain [0 5] are
The angles of the tangent line are always less than π/2, therefore the slopes or their derivatives are always positive. 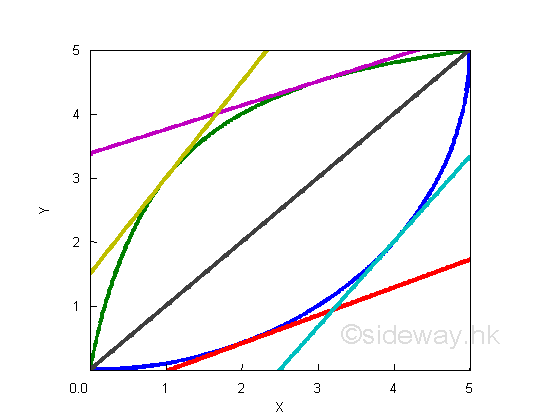
For a monotonically decreasing function y, the value of ratio Gy over Gx is always negative, therefore the value of derivaive is also always negative. The derivative of the straight line y=f(x)=-x is equal to -1. The derivatives of curves in domain [0 5] are
The angles of the tangent line are always greater than π/2, therefore the slopes or their derivatives are always negative. 
For a constant function y, the value of ratio Gy over Gx is always zero, therefore the value of derivaive is also always zero. Since the constant function is a horizontal line, the tangent line to the curve is a horizontal line also, the slopes or their derivatives are alway equal to zero. The slopes of curves, derivatives of functions y are: 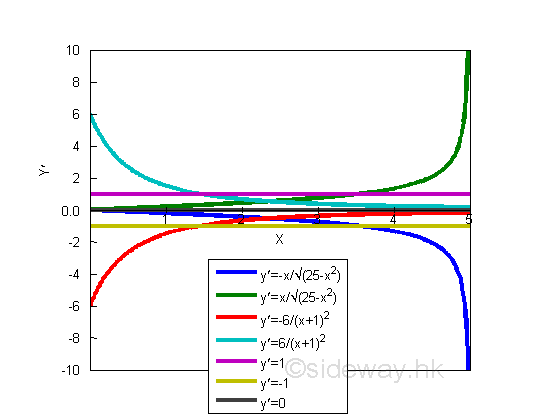
Therefore, the monotonicity can be determined by the sign of derivative.
ConcavityBesides the monotonicity, the concavity of the curve is also important. Similar to monotonicity, the slope of a curve can alway be increasing, i.e. becomes more positive or less negative, remaining constant, or alway be decreasing, i.e. becomes less positive or more negative. Constant values can also be positive, negative and zero, these values represent the slope of the functions of straight lines. But when considering increasing and decreasing values, they can be described by the concavity. Therefore, for a positive slope, if the value of slope is getting smaller or not increaseing as x increases, the curve is concave down or concave. And if the value of slope is getting larger or not decreaseing as x increases, the curve is concave up or convex. Similary, for a negative slope, if the value of slope is getting more negative as x increases, the curve is concave up or convex. And if the value of slope is getting less negative as x increases, the curve is concave down or concave. The shape of curves can refereed back to the original function y. And the slope of the slope, or the second derivatives of functions: 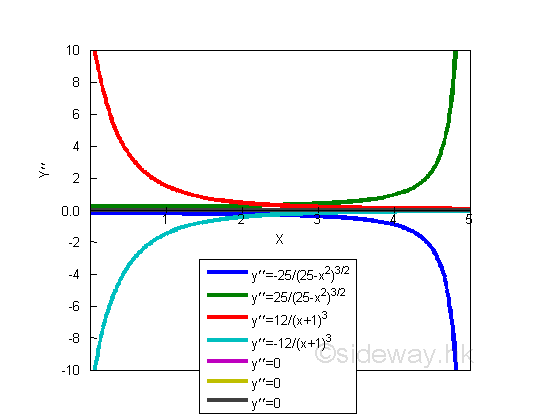
They can be summerized as:
The second derivatives of a convex, concave up curve is always positive because the slope of curve is always increasing. And the second derivatives of a concave, concave down curve is always negative because the slope of curve is always decreasing. A convex curve, e.g. y=2x2-10x+12.5 increases from negative slope to zero slope, and then to positive slope, the slope or first derivative of the curve is alway increasing and therefore the second derivative of the curve must be positive. The shape of second derivative only provides the rate of change information. imply: 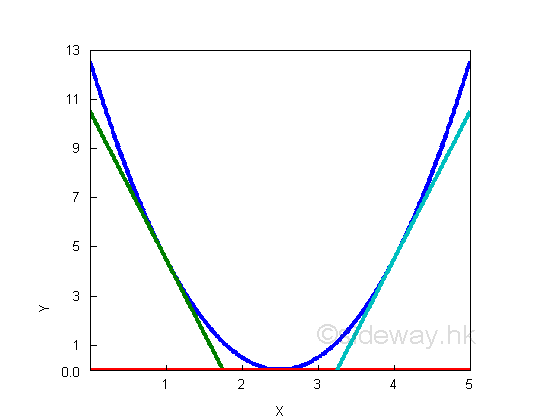
A concave curve, e.g. y=-2x2+10x decreases from positive slope to zero slope, and then to negative slope, the slope or first derivative of the curve is alway decreasing and therefore the second derivative of the curve must be negative. The shape of second derivative only provides the rate of change information. imply: 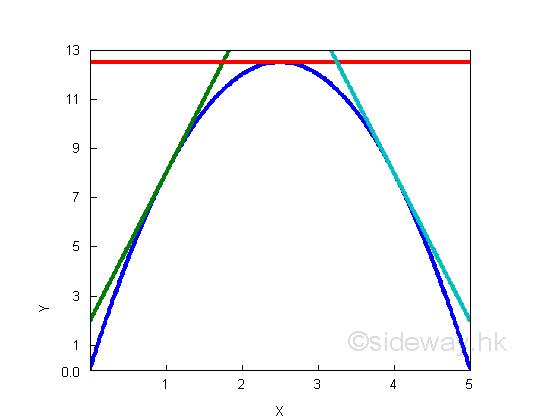
Local Extreme ValuesThe combination of two convex curves with negative and positive slopes forms a convex curve with a local or relative minimum. The combination two concave curves with positive and negative slopes forms a concave curve with a local or relative maximum. These values are related values because they are comparing with their neighborhood value, and these values may not be the absolute or global minumum or absolute or global maximum values of the function. For example a damped oscillation, y=5+5e-0.2xcos(5x) in the domain [0,∞), there are infinite number local minima and maxima and there are only one absolute minimum y=0.59 at x=0.628 and one absolute maximum, y=10 at x=0. 
According to the convex and concave curves, the slopes of the curves at both local minimum and local maximum are parallel to the horizontal x axis. The values of derivatives at local minimum and local maximum are equal to zero. Therefore the characteristic of a local minimum and local maximum are the first derivative of the function is equal to zero. However there also exists some functions that the derivatives of these functions at the position of local maximum or local minimum do not equal to zero. Besides, the derivative of a function is equal to zero does not guarantee a local maximum or a local minumum. The combination of a concave curve with negative slope and a concave curve with positive slope or a convex curve with positive slope and a convex curve with negative slope forms a curve with a sharp point. e.g. y=(x2+7.5x-25)1/2 or 5-(x2+7.5x-25)1/2. And the combination of straight lines with positive slope and negative slope or the combination of straight lines with negative slope and positive slope. e.g. y=|x-2.5| or y=2.5-|x-2.5|. 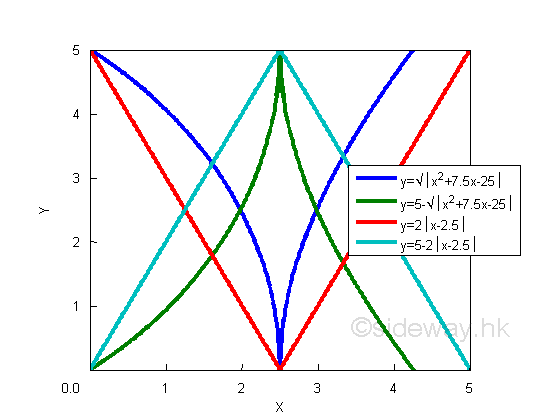
The sharp point formed by two curves with common vertial tangent is call vertial cusp. And the sharp point formed by two curves with no common tangent is call salient point or corner. These function have either local maximum or local minimum position in the curve, but their derivatives at these positions are not equal to zero. The direct calculation of the derivative is undefined at these positions. Although the derivative at these positions does not exist, the left and right derivatives of the functions exist at these positions. As these functions are not differentiable, these functions are not considered. The combination of a concave curve with positive slope and a convex curve with positive slope or a convex curve with negative slope and a concave curve with negative slope forms a smooth curve with a point of inflexion. e.g y=(x-2.5)3+15 or y=15-(x-2.5)3 
The turning point of the curve is called the point of inflextion. Althrough the derivative at position x=2.5 is equal to zero, the value of the function is neither a local maximum or a local minimum. Therefore the derivative at position equal to zero does not guarantee a local maximum or local minimum at that point. Or functions can have a horizontal tangent at a point that is neither a local maximum nor local minimum at that point. Therefore, in order to confirm whether there is a local maximum or a local minimum at a point, the tangent of its neighborhood points should be checked. For a local maximum at position x, 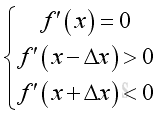
For a local maximum at position x, 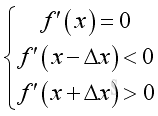
However the tangent of the point of inflexion is also not always equal to zero or parallel to the horizontal axis. e.g. y=5/(1+10-(x-2.5)) or y=5/(1+0.1-(x-2.5)). Or y=x1/3 on real for a point of reflexion with vertical tangent. 
The main difference between point of inflexion and local maximum or local minimum is the combination of curves. Because a curve is constructed by joining a convex curve and a concave curve in either ways, the point of inflexion is always the turning point of curve. The slope of the curve is always either positive slope or negative slope. Since the rate of change of slope of a convex curve is always increasing and the rate of change of slope of a concave is always decreasing, the first derivative of the function or the slope at the point of inflexion is either the local maximum or the local minimum. Therefore the second derivative of the function or the slope of the slope at the point of inflexion should always be equal to zero. 
However, a position of function with both the first derivative of the function and the second derivative of the function are equal to zero also can not guartente the position is a point of inflexion also. e.g. y=x4. The position of function with first derivative equals to zero and second derivative equals to zero is a local minumum instead of a point of inflexion. 
Therefore, for a point of reflection at position x, 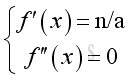
In general, if the graph of function is a concave curve then for a local maximum at position x, 
And, if the graph of function is a convex curve then for a local minumum at position x, 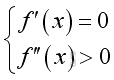
|
Sideway BICK Blog 29/09 |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
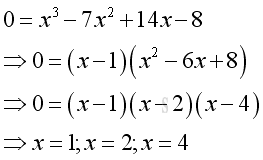
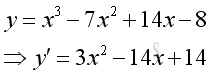
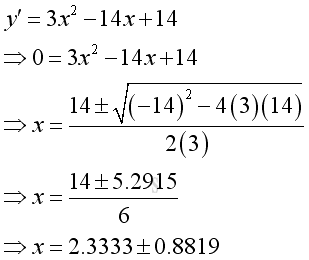
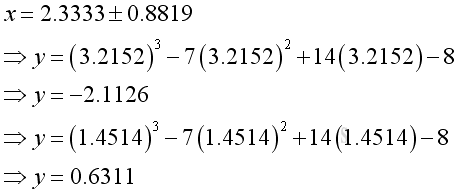
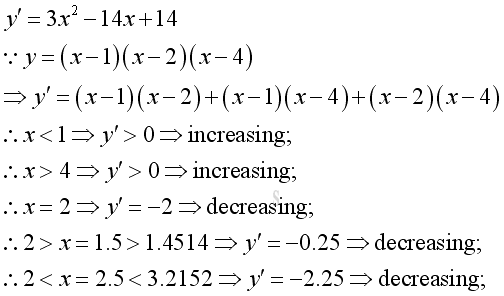

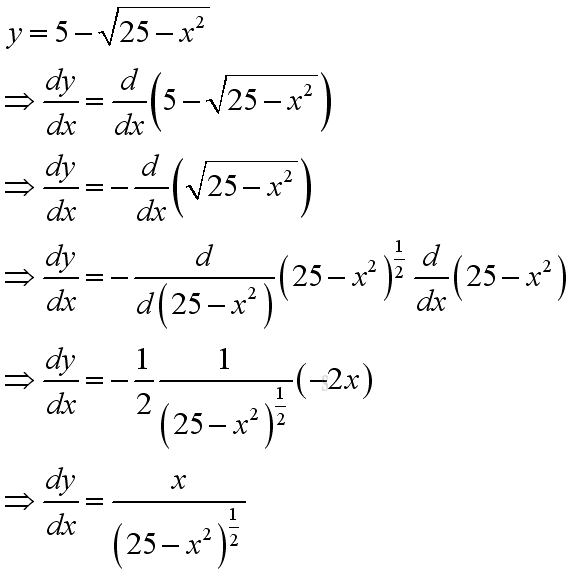 and
and
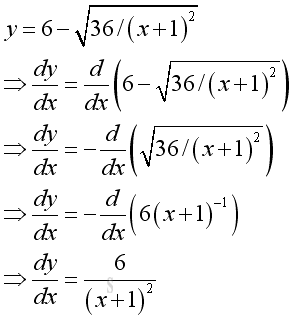
 and
and


