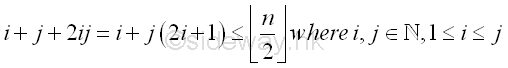Primes

A prime is defined as natural number that can only be divided by 1 and itself. For examples, numbers 2, 3, 5, 7,... are primes. Prime numbers are one of the important types of numbers but there is no easy way to identify or find prime numbers. 

Sieve of Eratosthenes

The sieve of Eratosthenes is a simple ancient algorithm developed by Eratosthenes to identify all prime numbers by eliminating all multiples of found primes in any given limit, n iteratively.

1	2	3	4	5	6	7	8	9	10
11	12	13	14	15	16	17	18	19	20
21	22	23	24	25	26	27	28	29	30
31	32	33	34	35	36	37	38	39	40
41	42	43	44	45	46	47	48	49	50
51	52	53	54	55	56	57	58	59	60
61	62	63	64	65	66	67	68	69	70
71	72	73	74	75	76	77	78	79	80
81	82	83	84	85	86	87	88	89	90
91	92	93	94	95	96	97	98	99	100
…	…	…	…	…	…	…	…	…	…

The concept of the sieve of Eratosthenes is simple but the sieve method is more complicated to be implemented.

• The first step to generate an incremental sequence of positive consecutive integers with n elements.

• Since number 1 is neither prime nor composite, number 1 is ignored by the sieve.

• As number 2 is the smallest number in the list, by definition, number 2 must be the first prime of the incremental sequence.

• The sieving mechanism is to cross off all multiples of found prime in the list of remaining numbers iteratively.

• According to the mechanism of sieve of Eratosthenes, only the remaining numbers on the list are sieved. In other words, the first multiple of the prime p to be cross off is equal to p as all multiples smaller than prime p have already been sieved by those found primes smaller than p. And therefore the last or largest sieving prime p is also limited to the floor of square root of n because all multiples of primes after have already been crossed off.

• However, there is no simple way to prevent the repeating crossing off problem as crossing out the number in the table of sieve of Eratosthenes.

• Primes less than or equal to a given limit n are in the list of the remaining numbers after sieving

Sieve of Sundaram

The sieve of Sundaram is a simple deterministic algorithm developed by Sundaram in 1934 for determining all prime numbers except number 2 up to any given n by eliminating all number of the form i+j+2ij within the limit, the floor of (n-1)/2 iteratively and then doubling and increaseing the remaining numbers by one. The two typical ideas are the elimintion of even numbers which are divisible by number 2 and all odd numbers except number 1 are expressed as an arithmetic progression. For example, numbers eliminated in n=200 with limit equals to 99.

1	2	3	4	5	6	7	8	9	10
11	12	13	14	15	16	17	18	19	20
21	22	23	24	25	26	27	28	29	30
31	32	33	34	35	36	37	38	39	40
41	42	43	44	45	46	47	48	49	50
51	52	53	54	55	56	57	58	59	60
61	62	63	64	65	66	67	68	69	70
71	72	73	74	75	76	77	78	79	80
81	82	83	84	85	86	87	88	89	90
91	92	93	94	95	96	97	98	99

 

Determined primes are

1	2	3	4	5	6	7	8	9	10
11	12	13	14	15	16	17	18	19	20
21	22	23	24	25	26	27	28	29	30
31	32	33	34	35	36	37	38	39	40
41	42	43	44	45	46	47	48	49	50
51	52	53	54	55	56	57	58	59	60
61	62	63	64	65	66	67	68	69	70
71	72	73	74	75	76	77	78	79	80
81	82	83	84	85	86	87	88	89	90
91	92	93	94	95	96	97	98	99	100
101	102	103	104	105	106	107	108	109	110
111	112	113	114	115	116	117	118	119	120
121	122	123	124	125	126	127	128	129	130
131	132	133	134	135	136	137	138	139	140
141	142	143	144	145	146	147	148	149	150
151	152	153	154	155	156	157	158	159	160
161	162	163	164	165	166	167	168	169	170
171	172	173	174	175	176	177	178	179	180
181	182	183	184	185	186	187	188	189	190
191	192	193	194	195	196	197	198	199	200

The sieving concept of sieve of Sundaram is similar to the crossing off composite numbers mechanism used in sieve of Eratosthenes. Instead of sieving the whole list of the given limit n, sieve of Sundaram only sieves the odd number of the list, and all odd numbers except number 1 are rearranged in an increasing order from one to floor of n/2. 

• Since number 1 is neither prime nor composite, number 1 is ignored by the sieve.

• The first step to generate an incremental sequence of positive consecutive integers with floor of n/2 elements starting from one to floor of n/2 to represent all odd numbers except number 1.

• The sieving mechanism is to cross off all numbers of the form i+j+2ij where 1≤i≤j, in the list of remaining numbers iteratively. The form is

  

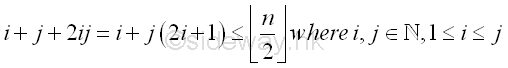
• Although, all even numbers are excluded in the list, there is still no simple way to prevent the repeating crossing off problem as crossing out the number in the table of sieve of Sundaram as in sieve of Eratosthenes.ber 1 is ignored by the sieve.

• Primes less than or equal to a given limit n are obtained by doubling all remaining numbers in the list of the after sieving and then increasing all numbers by one.

The sieve of Sundaram is based on sieving the composite odd numbers since all even numbers are ignored. Since an odd number can be expressed as 2k+1, the odd number sequence can therefore be expressed as an ordered sequence in term of k. Let 2i+1 and 2j+1 be any two odd numbers. Therefore any composite odd number can be expressed as (2i+1)(2j+1)=2(i+j+2ij)+1. In other words, all composite number with sequence number k equal to i+j+2ij must be composite odd numbers. Since the sieving mechanism is an iterative operation to sieve all possible composite odd number in the list. The remaining sequence numbers in the list must be prime odd numbers.  

Sieve of Atkin

The sieve of Atkin is a simple algorithm developed by Atkin and Bernstein in 2004 to find all prime numbers by eliminating all multiples of number 2, 3, and 5, and testing iteratively with an irreducible binary quadratic equation to which the numbers of solution must be odd providing that the number is a squarefree numbers, in any given limit, n. The first part of the algorithm making use of the idea of sieve of Eratosthenes to eliminate must of the composites which are multiples of number 2, 3, and 5, in the list. The second part of the algorithm making use of the properties of the irreducible binary quadratic form of a number to test where a number is a squarefree composite or not, instead of checking the divisibility of a number.

1	2	3	4	5	6	7	8	9	10
11	12	13	14	15	16	17	18	19	20
21	22	23	24	25	26	27	28	29	30
31	32	33	34	35	36	37	38	39	40
41	42	43	44	45	46	47	48	49	50
51	52	53	54	55	56	57	58	59	60
61	62	63	64	65	66	67	68	69	70
71	72	73	74	75	76	77	78	79	80
81	82	83	84	85	86	87	88	89	90
91	92	93	94	95	96	97	98	99	100
101	102	103	104	105	106	107	108	109	110
111	112	113	114	115	16	117	18	119	120
121	122	123	124	125	26	127	28	129	130
131	132	133	134	135	36	137	38	139	140
141	142	143	144	145	46	147	48	149	150
151	152	153	154	155	56	157	58	159	160
161	162	163	164	165	66	167	68	169	170
171	172	173	174	175	76	177	78	179	180
181	182	183	184	185	86	187	88	189	190
191	192	193	194	195	96	197	98	199	200
…	…	…	…	…	…	…	…	…	…

Remaining numbers are divided into 3 groups with each number congruent to 1 modulo 4, 1 modulo 6, and 11 modulo 12. In order to have a common arithmetic progression, three sets of modulo 60 residues are {1,13,17,29,37,41,49,53}, {1,7,13,19,31,37,43,49}, and {11,23,47,59} .