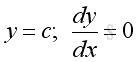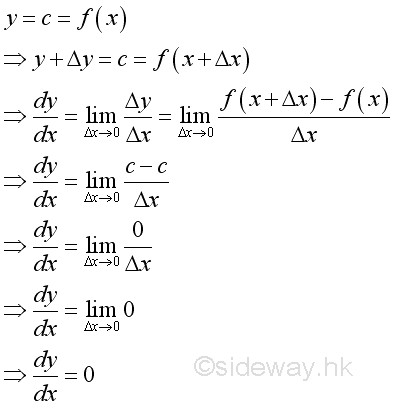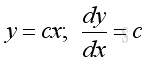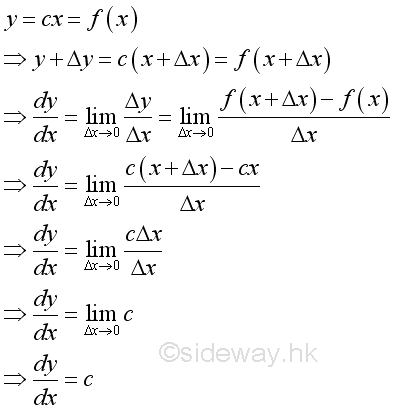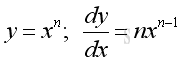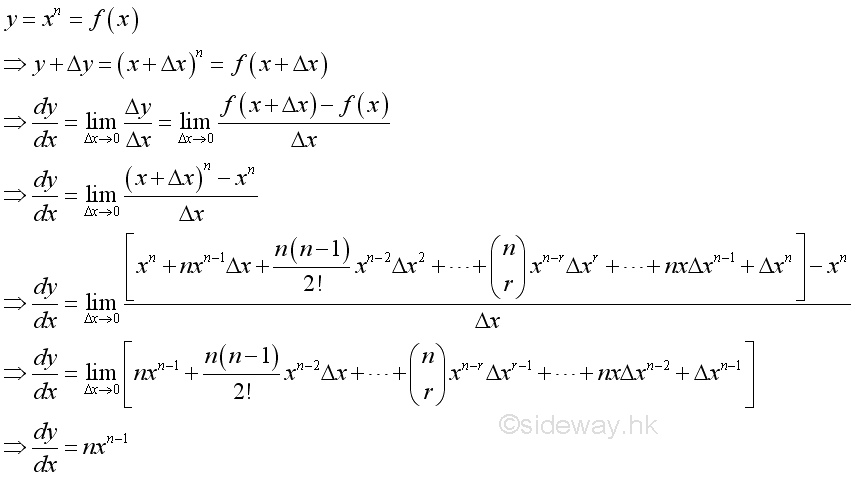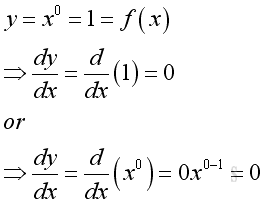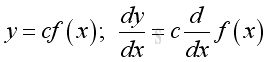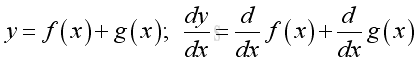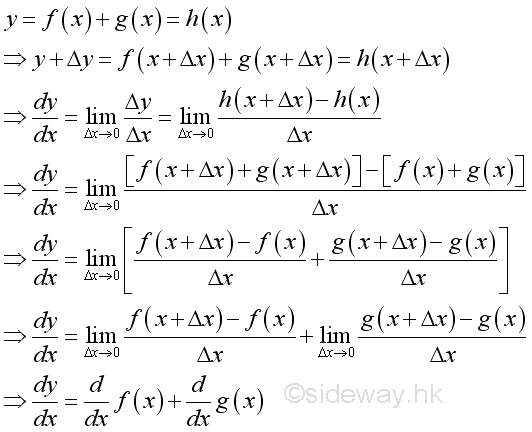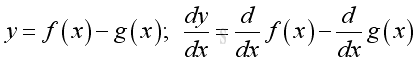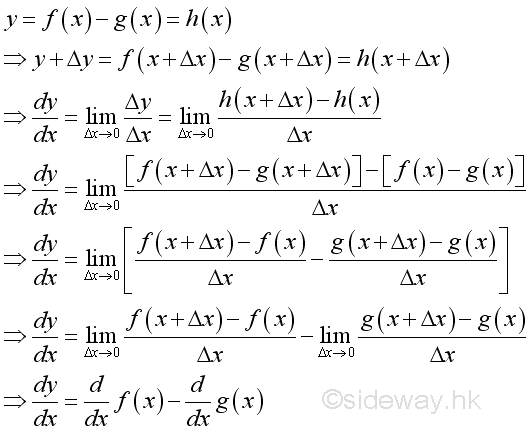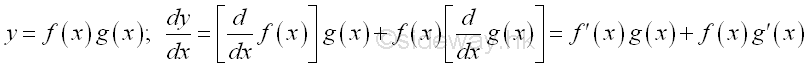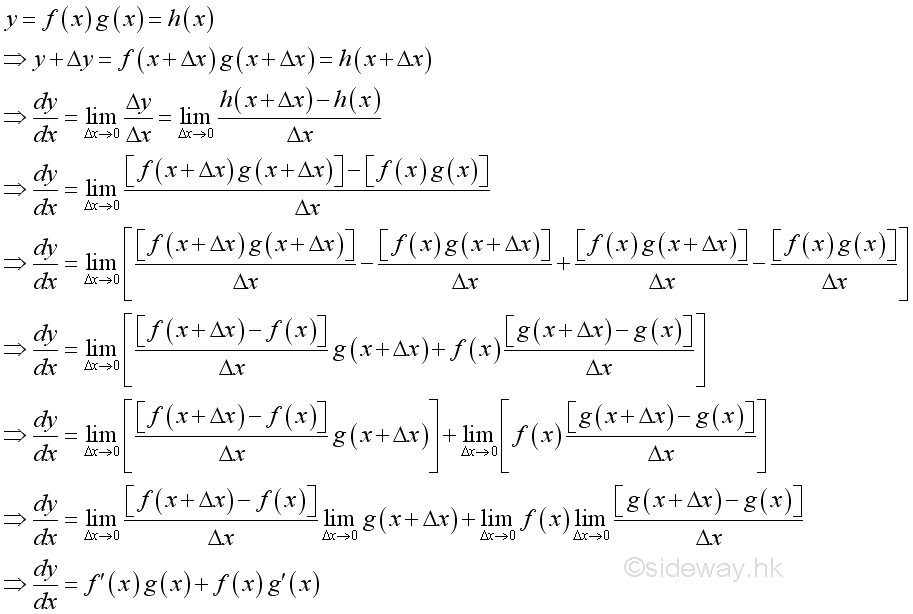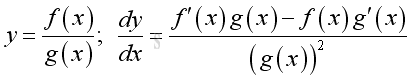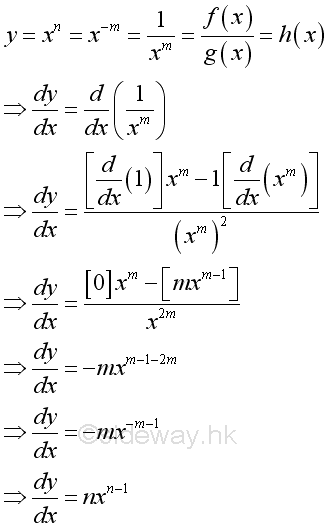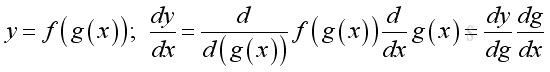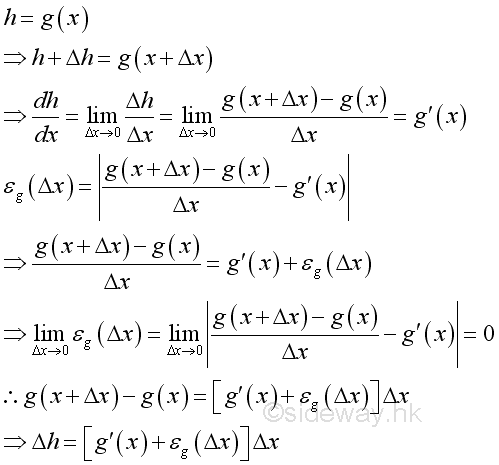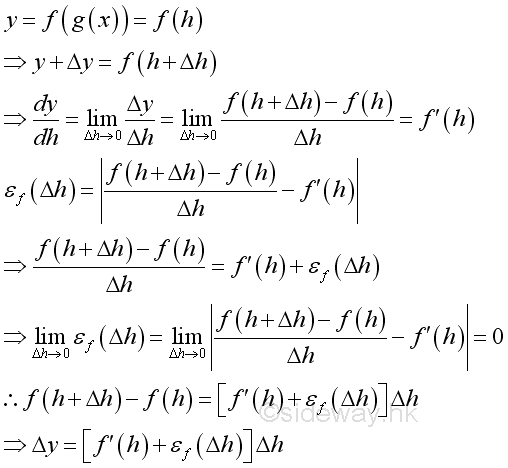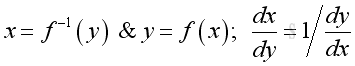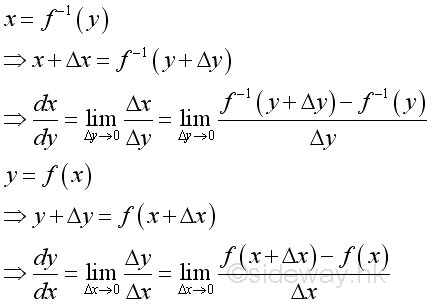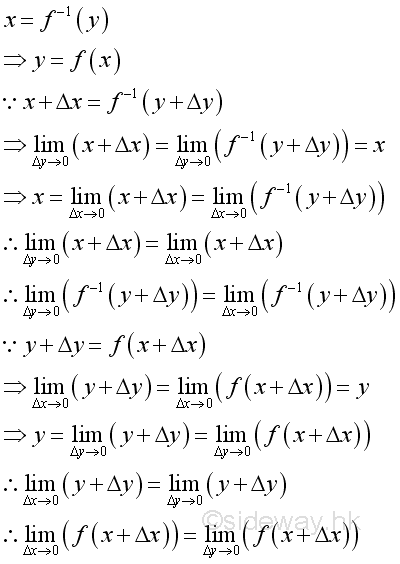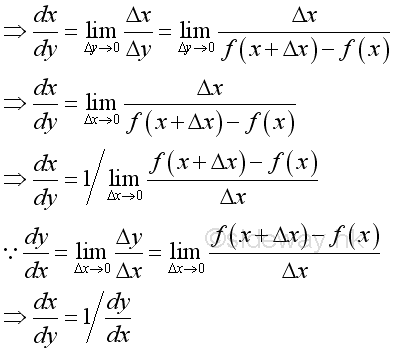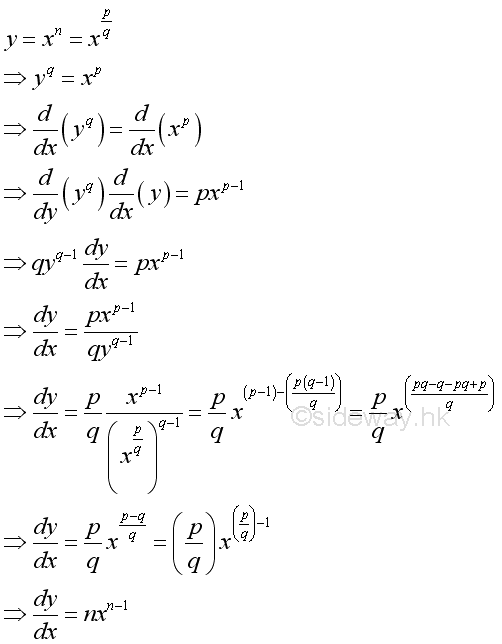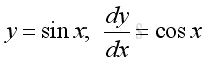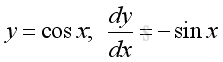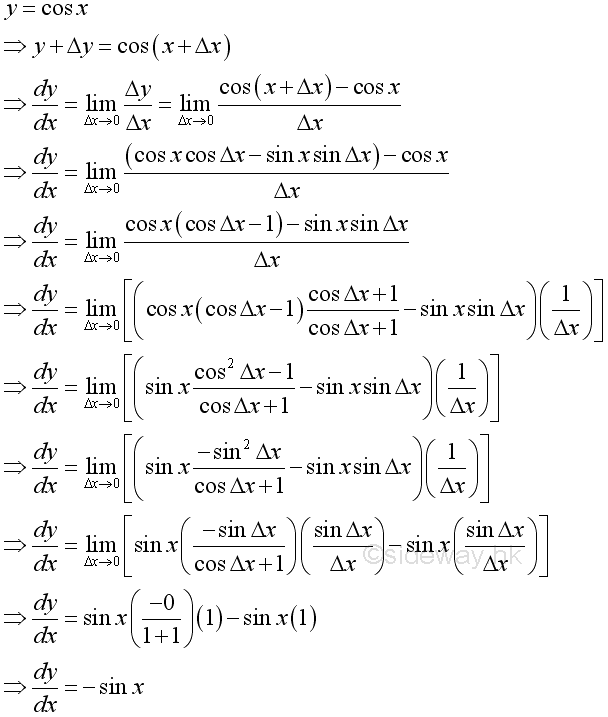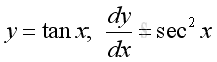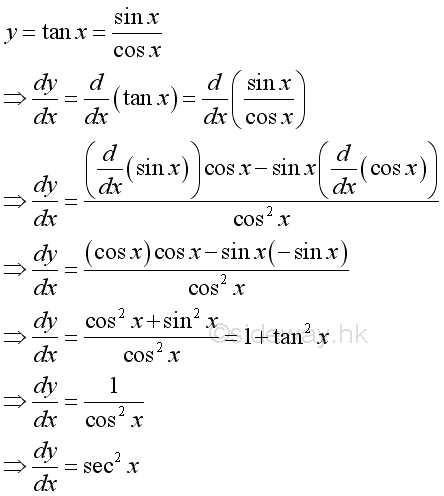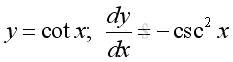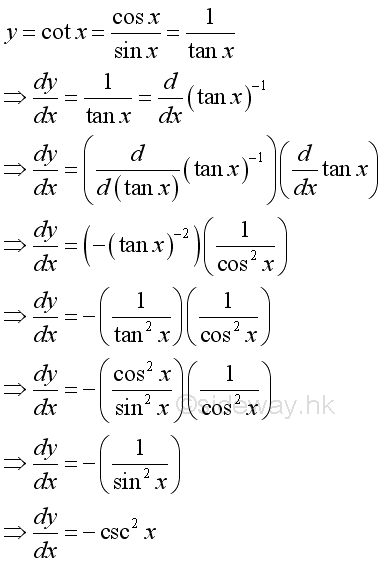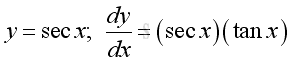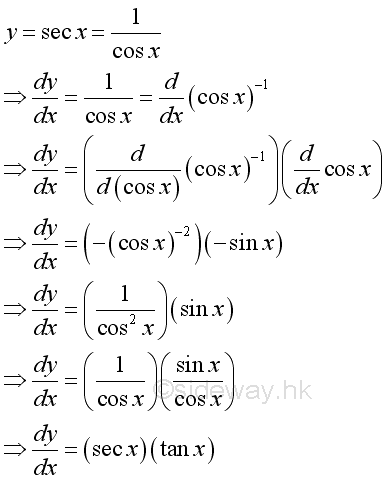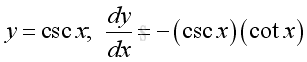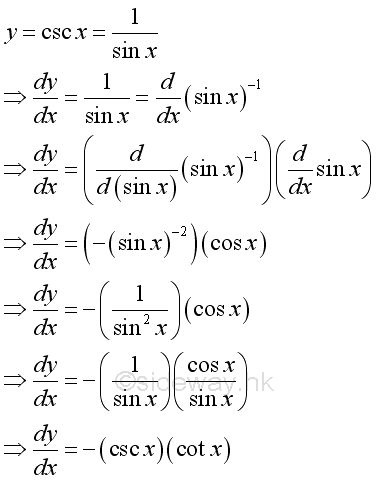Sideway
BICK BLOG from Sideway
Sideway
BICK BLOG from Sideway
|
Link:http://output.to/sideway/default.asp?qno=110900005 Rules of Differetiation, Polynomial Rules of DifferentiationIn order to simplify the task of finding derivatives, some general rules are developed to help finding derivatives with having to use the defination directly. Derivatives of Polynomials
Link:http://output.to/sideway/default.asp?qno=110900006 Trigonometric Derivatives of Trigonometric FunctionsTrigonometric functions are very important in practical application. Trigonmetric function f is continuous when it is defined at every real numbers x in the domain. To determine the derivatives, the real number x is the angle of the trigonometric function and is measured in radian. Limits and Trigonometric FunctionsTrigonometric functions are functions of an angle. The three basic are sine cosine and tangent. The geometric definition of trigonometric functions can be related by sides of a triangle. One important limit related to finding derivatives of trigonometric functions is the ratio of value of a trigonometric function to the angle of the trigonometric function. Geometrically, the trigonometric functions can represented by constructing triangles in a unit circle with radius r=1. 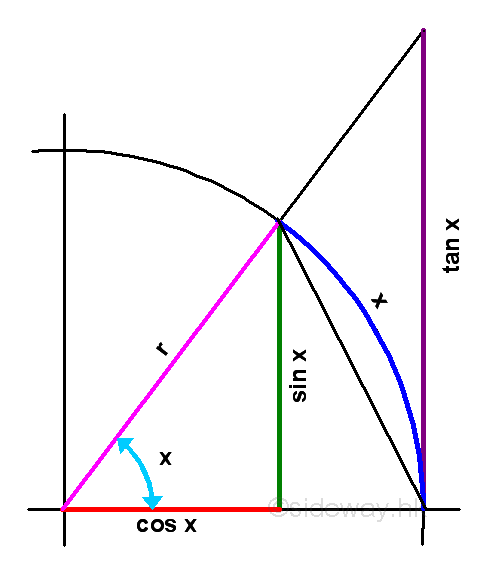
Limits and Sine FunctionAccording to the graph, consider the angle x in radian between 0 and π/2 when x approaching zero and not equal to zero, the relationship of the area of triangle w/sin x, the area of circular sector w/arc x, and the area of triangle w/tan x are: 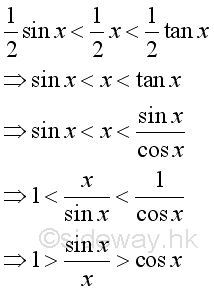
As x decrease, cos x will increase. (sin x)/x will increase also but less than 1. Imply as x approach +0, limit of (sin x)/x exists. Rearrange the inequality: 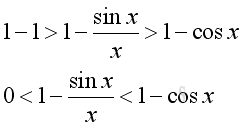
As x approach +0, i.e. δ>x>0 imply: 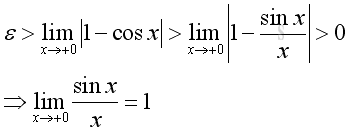
Similarly as x approach -0, imply: 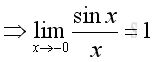
Therefore: 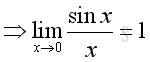
Limits and Cosine FunctionAnother important limit is: 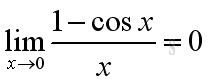
Since cosine function and sine function are related by a right angle triangle and both functions are continuous in every numbe of the domain, the cosine function can be transformed through algebraic manipulations: 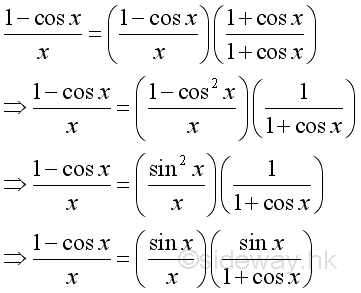
The limit of the function can be determined by: 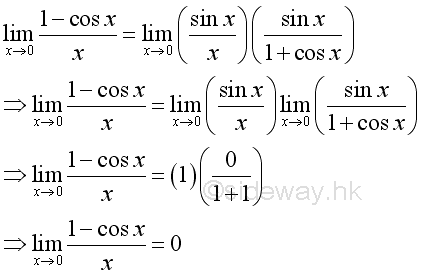
Plots of Limits and Trigonometric FunctionsThe inequality, limits and trigonometric functions can be plotted as in the following figure: 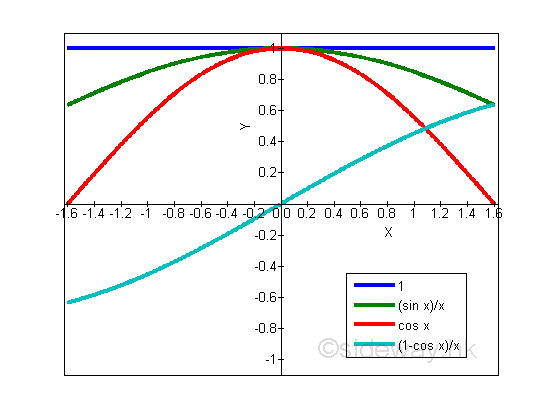
Derivatives of Trigonometric Functions
|
Sideway BICK Blog 12/09 |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||