Derivatives of Implicit Equations

Functions are usually defined in terms of another variable explicitly. It is called y is a function of x and can be expressed as an explicit function, y=f(x).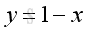

The explicit function can also be described as a relation between x and y implicitly.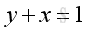

Sometime an implicit equation can be transformed into an explicit equation easily.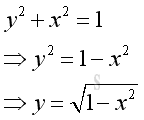

But, sometime it is not an easy job to transform an implicit equation into an explicit equation.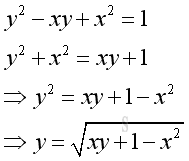

Derivatives of Implicit Equations

For a simple implicit equation the derivative of function y can be obtained by transforming into an explicit equation.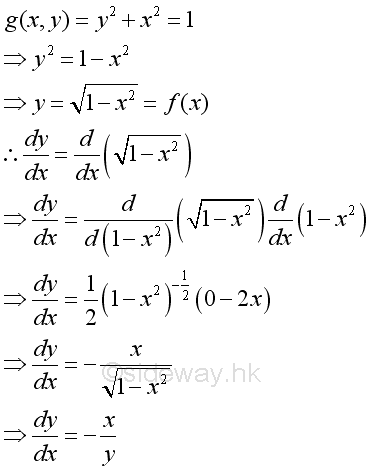

Similarly the derivative of function y can also be obtained from an implicit equation directly.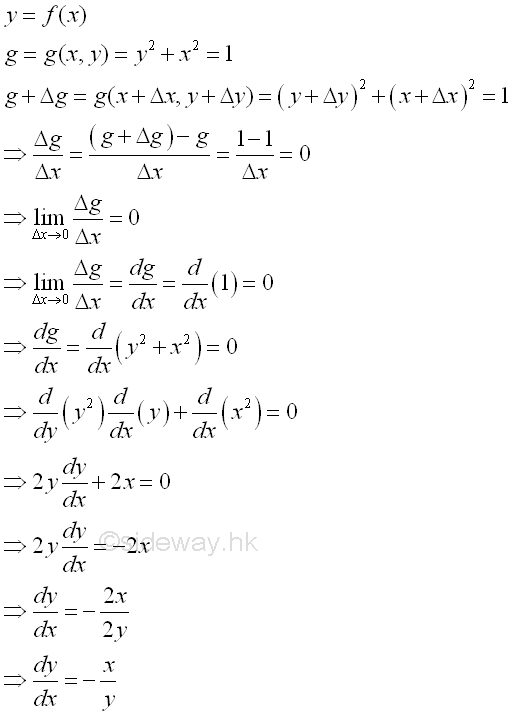

For any implicit equation, the derivative of function y can be derived from the first principal.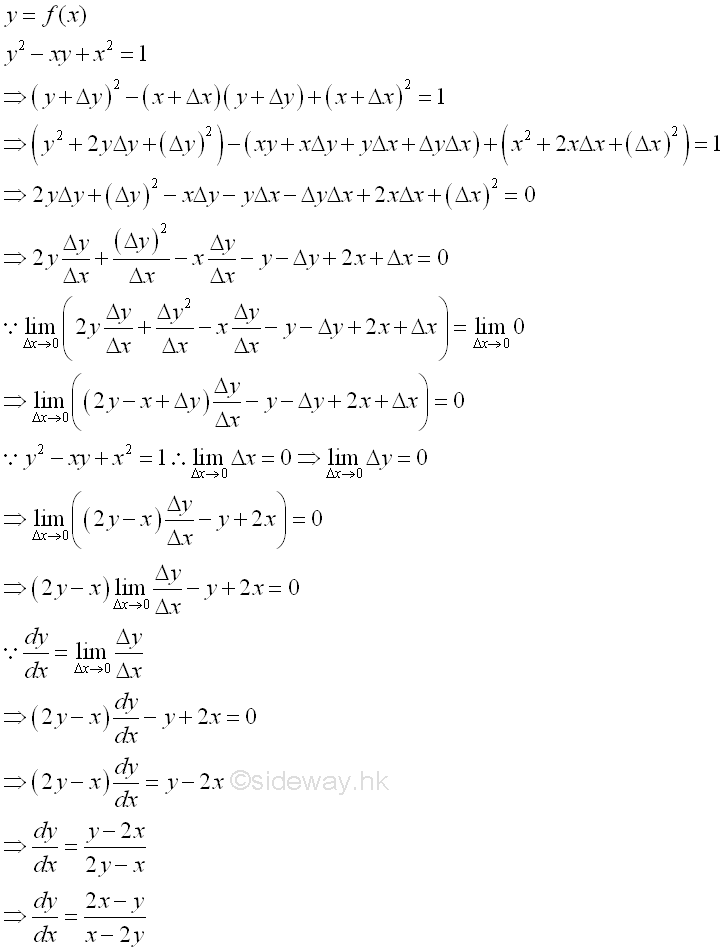

Similarly for any implicit equation, the derivative of function y can be derived from the rules of differentiation.

Since an implicit equation can be considered as a function g(x,y) composed of p(x), q(f(x)) and r(x,f(x)), therefore for any implicit equation, the derivative of function y can be derived from the rules of differentiation by differentiating both sides of the equation. In the above examples the RHS  is constant, the derivatives with respect to x is therefore equal to zero. The derivatives can then be obtained by solving the resulting equation. This is call mehod of implicit differentiation. And the above examples are assumed y is a differentiable function of x.