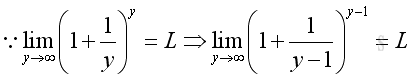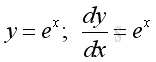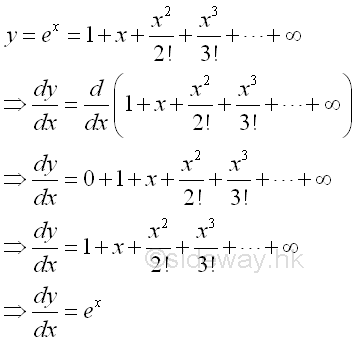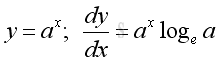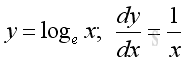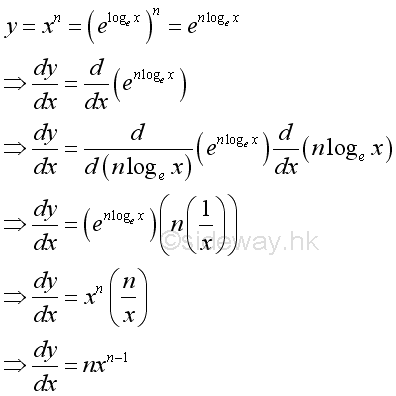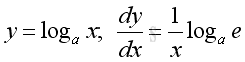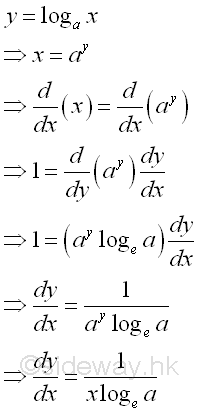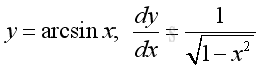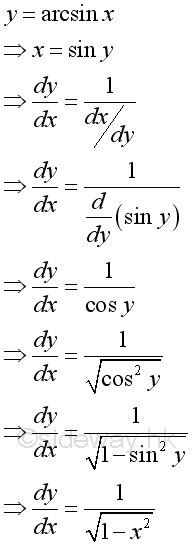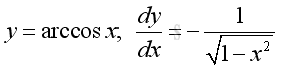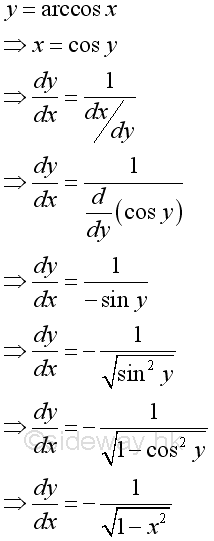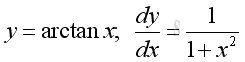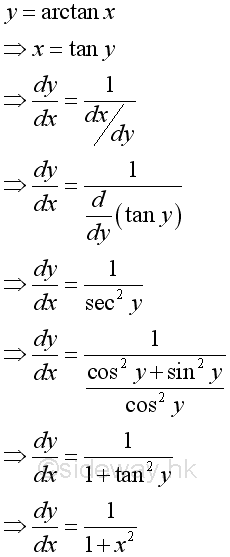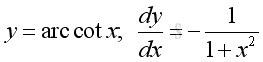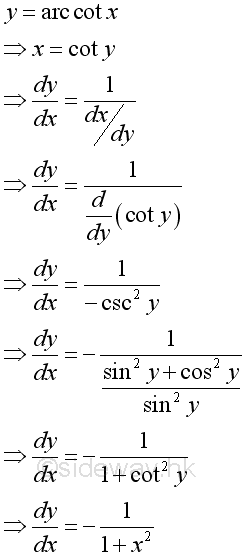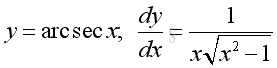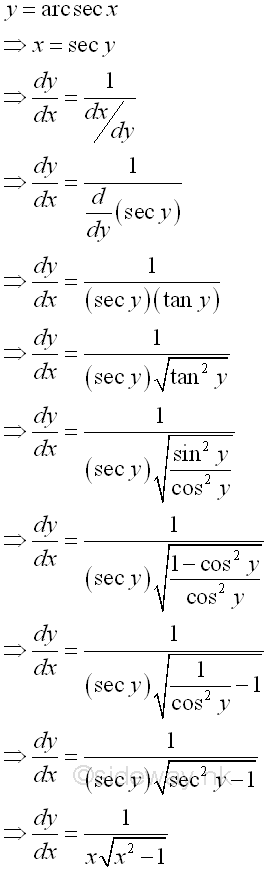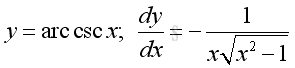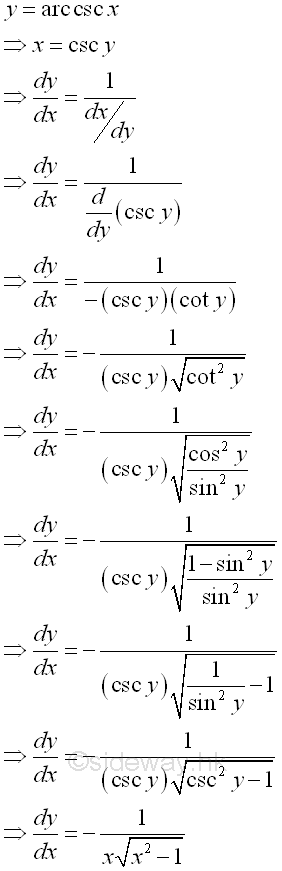Sideway
BICK BLOG from Sideway
Sideway
BICK BLOG from Sideway
|
Link:http://output.to/sideway/default.asp?qno=110900007 Exp() and Log() Derivatives of Exponential and Logarithmic FunctionsBoth exponential and logarithmic functions are very important in real world problems. The natural exponential function ex has the base e. And the natural logarithmic function, ln(x) is the inverse of the natural exponential function. The constant e is an important constant in finding limits and derivatives also. Constant eThe number e is base of the natural logarithm. The number e is a constant sometimes known as Napier's constant, named after the Scottish mathematician John Napier who introduced logarithms. The mathematical constant e is also called Euler number with its symbol honors Swiss mathematician Leonhard Euler. The constant e is an irrational number. The numerical value of e to 10 decimal places is 2.7182818284. Definition of eThere are many ways to define the mathematical constant e. The number e can be defined as the limit of: 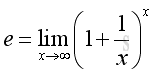
For x approaching +∞, there always exists a pair of integers such that: 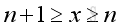
Imply: 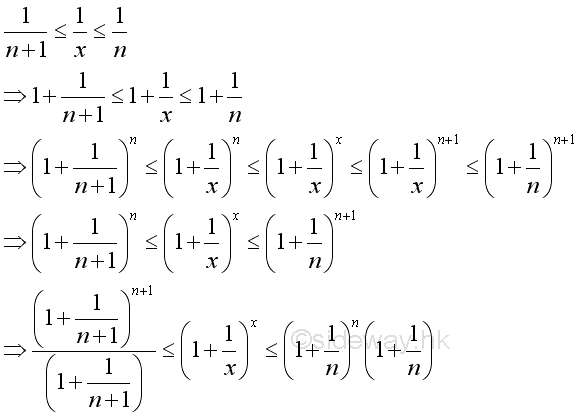
Since the following limits exist and are equal to 1:
Imply: 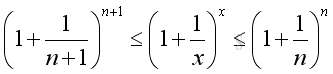
And if limits exist when n approaching +∞, that is:
Therefore the limit when x approaching +∞ can be proved by the limit when integer n approaching +∞. And using Binomial Theorem to expand the terms in the bracket of the limit goes up to n, where n approaching +∞: 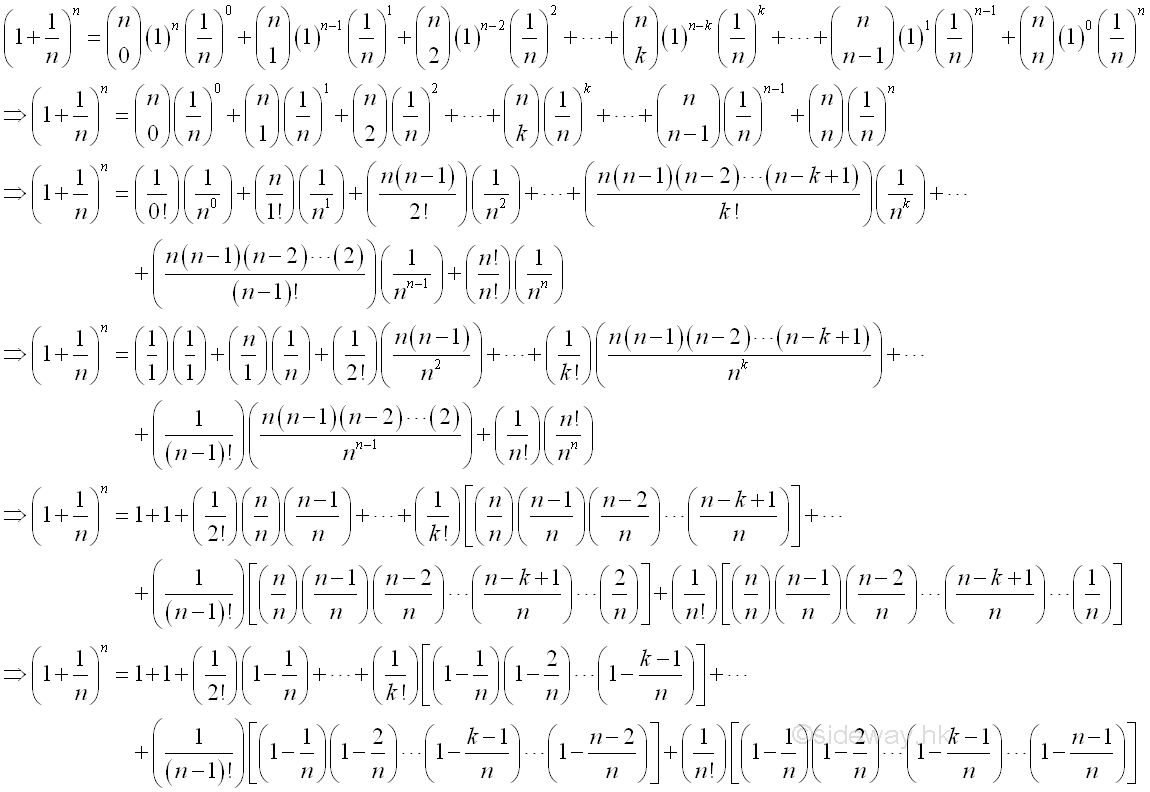
Therefore the limit when n approaching +∞ is: 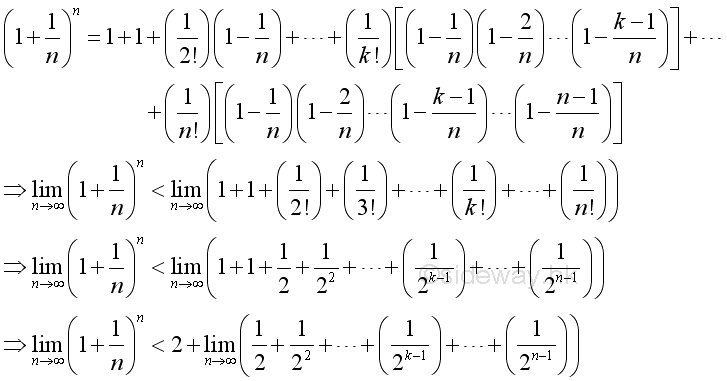
The limit on the RHS when n approaching +∞ is: 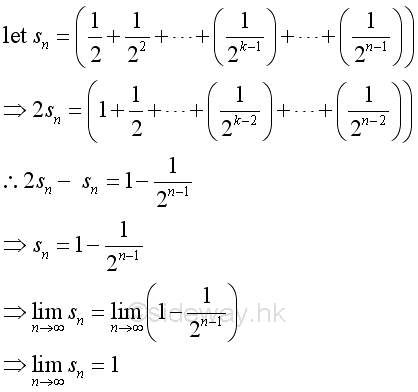
The limit on the LHS when n approaching +∞ exists: 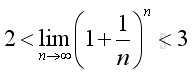
Therefore the limit of the series exists: 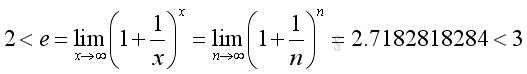
For x approaching -∞, let x=-y then: 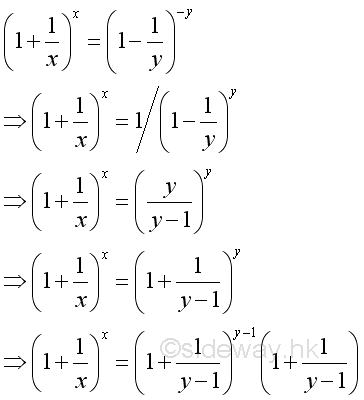
As shown before, when y approaching +∞, imply:
Therefore, when x approaching ∞, imply: 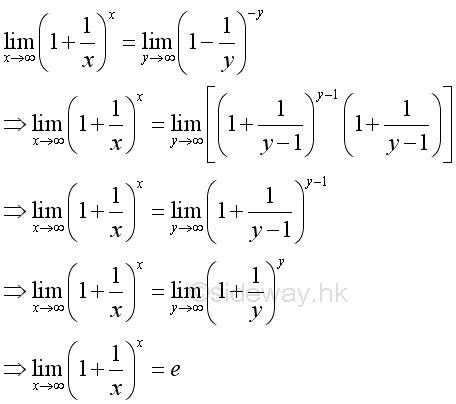
Another Definition of eSimilarly, the limit can be rewritten for x approaching 0, imply: 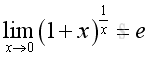
Define constant e as a sum of infinite seriesBesides, as shown in the binomial expansion, the limit can also be expressed as: 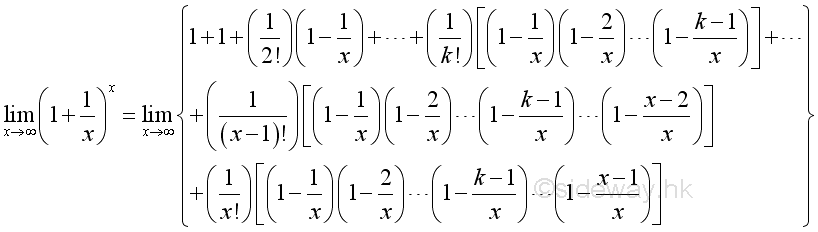
After rearrangement, imply: 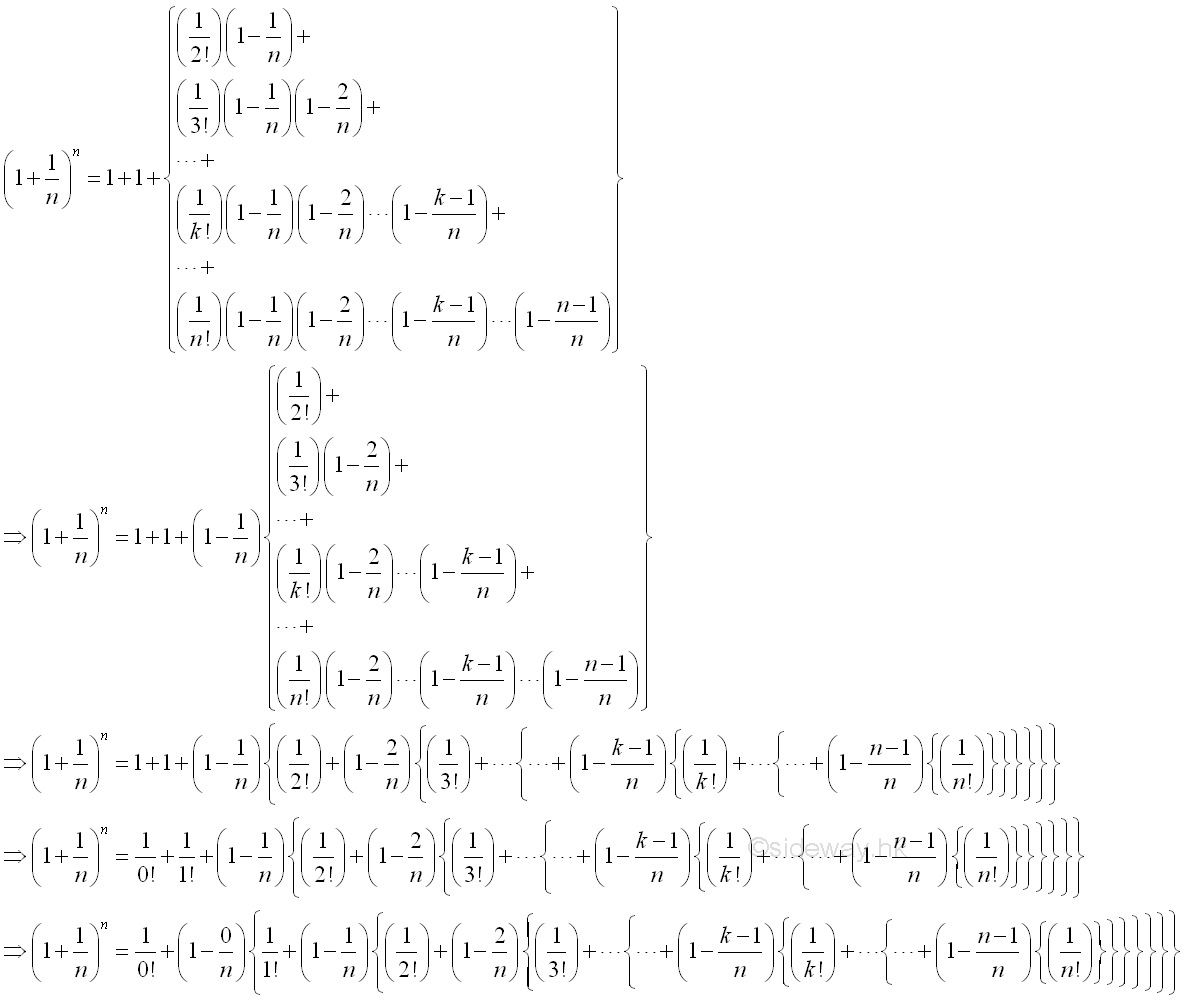
Consider the k term, when k=1: 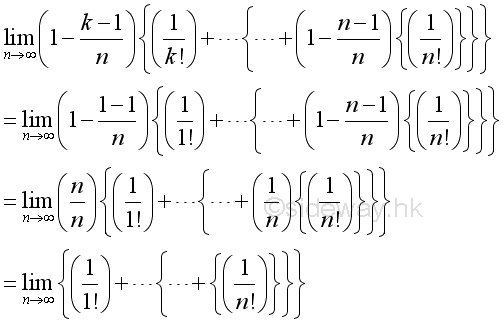
Consider the k term, when k=n-1: 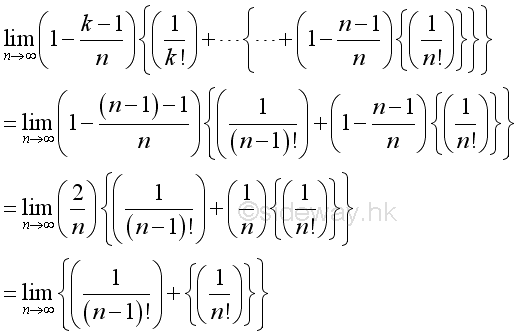
Therefore the numeric value of k term is bounded and since n approaching ∞, for every k there is a n term such that n>>k: 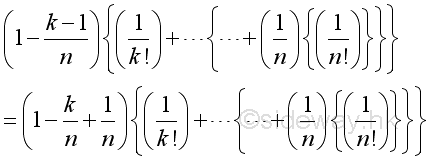
Imply when n approaching ∞, the limit of k term can be approximated by: 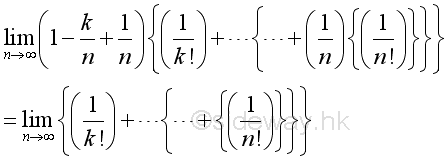
Therefore when x approaching ∞, the limit of can be approximated by: 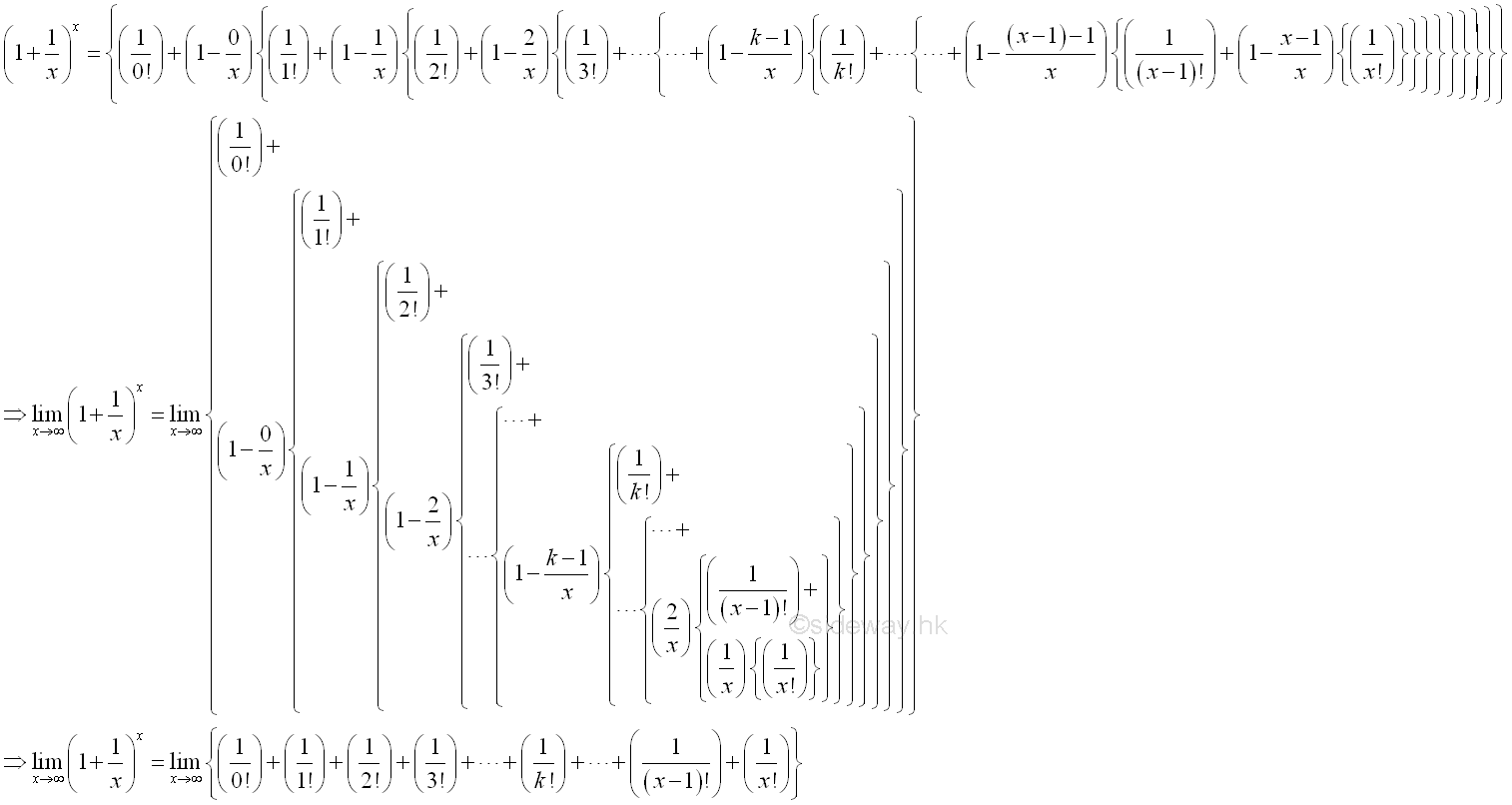
Imply: 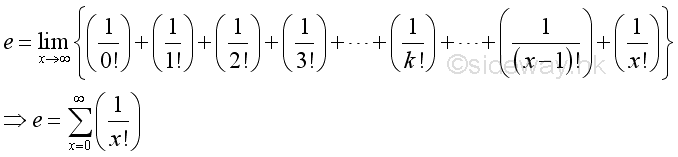
Definition of Natural Exponential FunctionThe Natural Exponential Function can be expressed as: 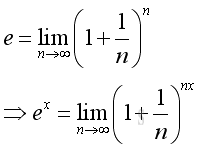
Let m=nx, since n approaching ∞, there must exist a numeric value such that m is an integer, imply: 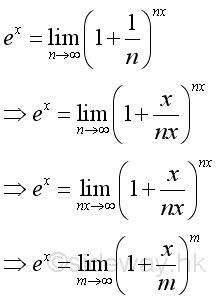
Using Binomial Theorem to expand: 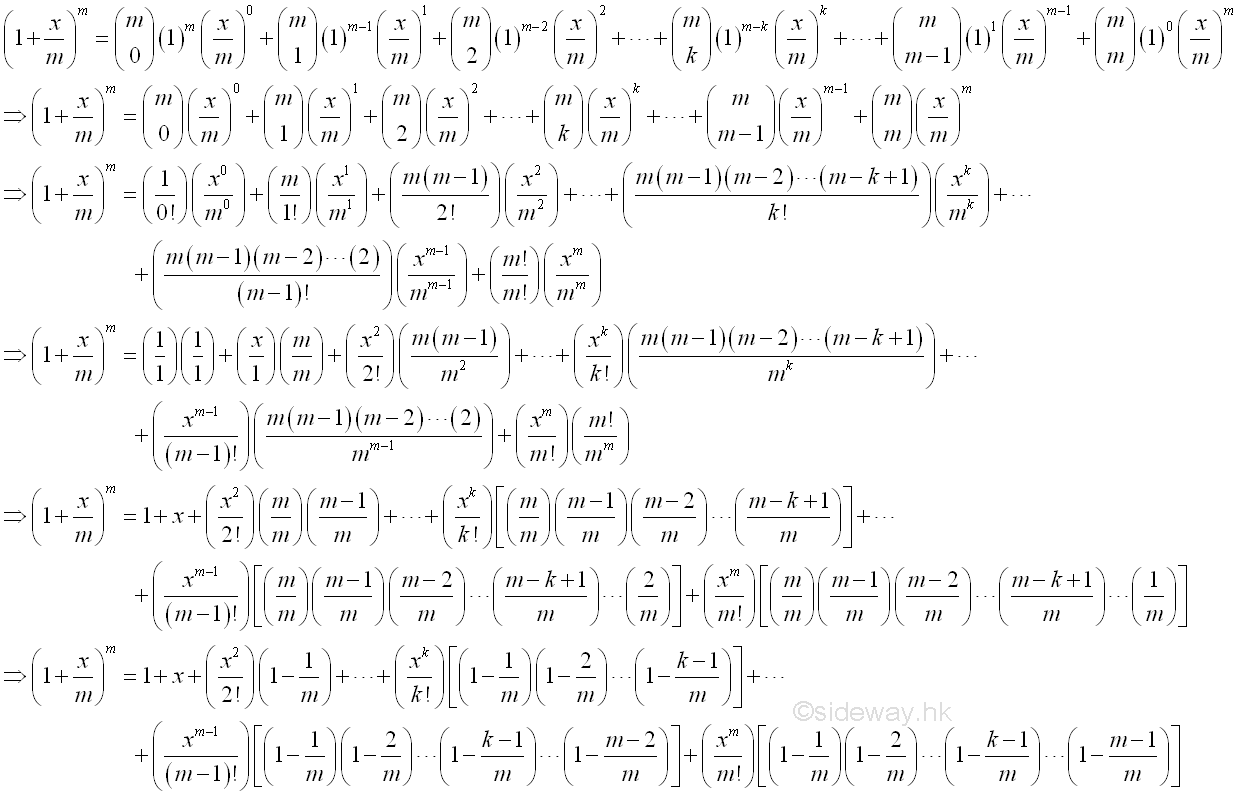
The limit is equal to : 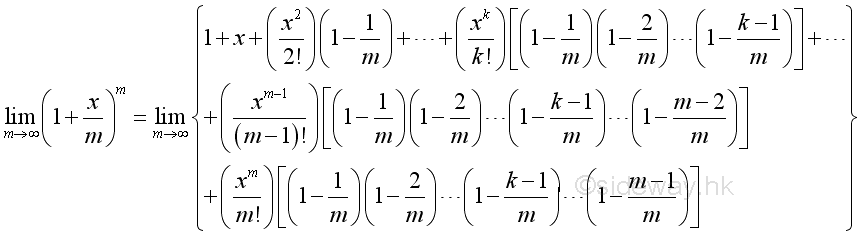
Similar to define the Euler number, the natural exponential function is equal to : 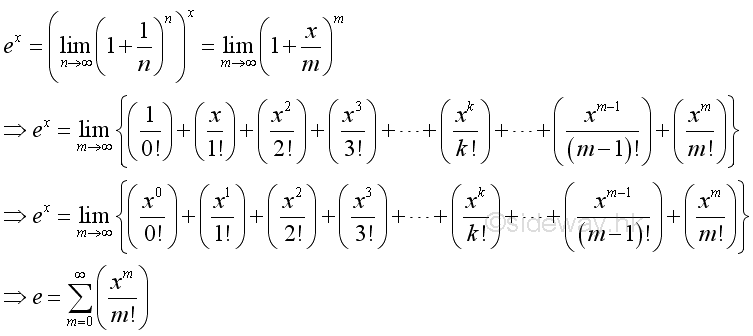
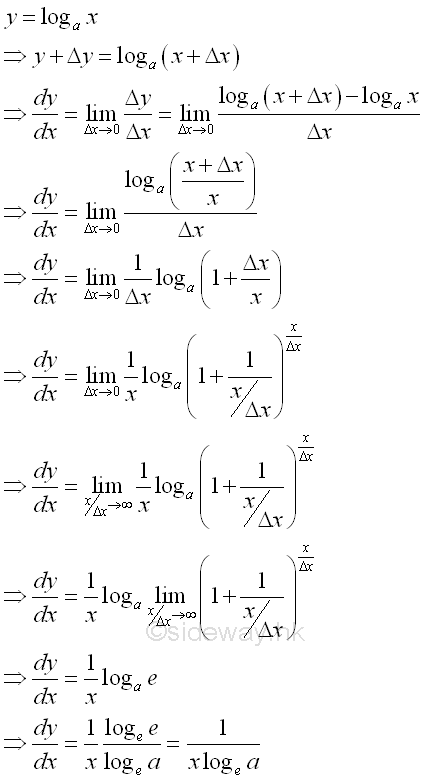
Derivatives of Exponential and Logarithmic Functions
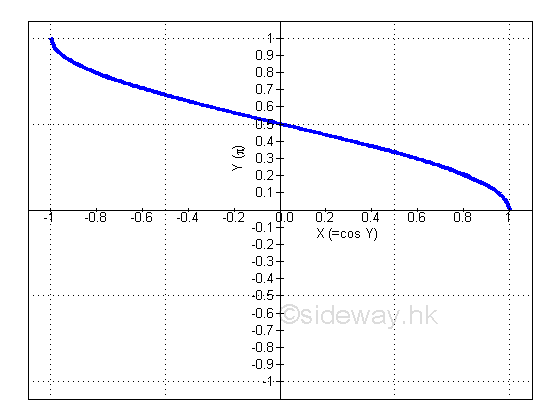
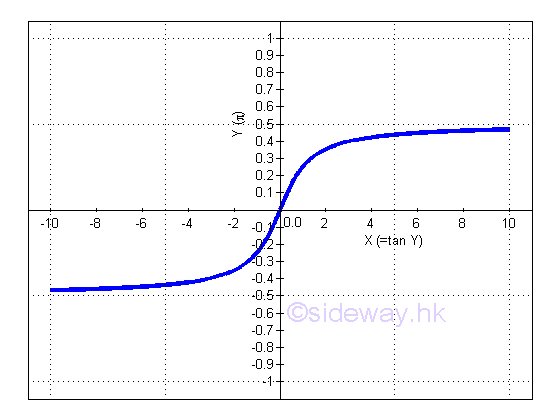
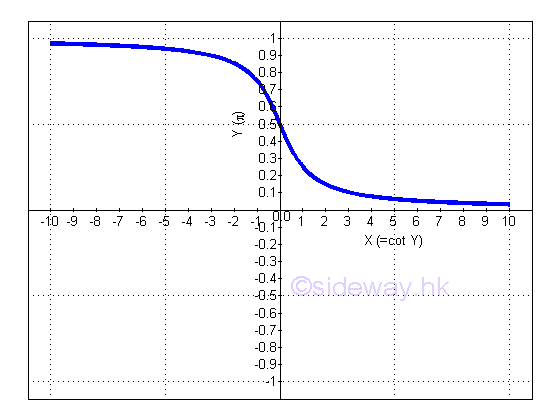
Link:http://output.to/sideway/default.asp?qno=110900008 Inv Trigonometric Derivatives of Inverse Trigonometric FunctionsInverse trigonometric functions are often found in real life applications. Derivatives of Inverse Trigonometric Functions
|
Sideway BICK Blog 16/09 |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
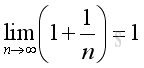 and
and
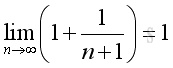
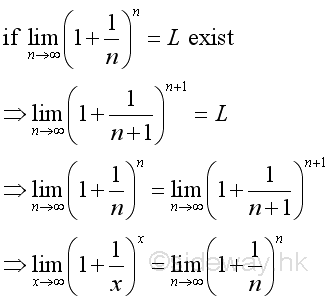
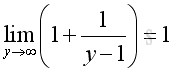 and
and