 Sideway
BICK BLOG from Sideway
Sideway
BICK BLOG from Sideway
|
Link:http://output.to/sideway/default.asp?qno=110900014 Linear Motion Instantaneous Rate of ChangeRate of change is the average change of function y=ƒ(x) between two instants, x and x+Δx. The derivative is the instantaneous rate of change by applying limit Δx to zero. 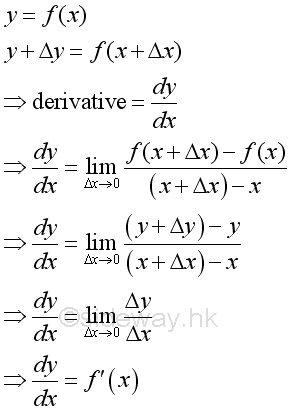
Linear Motion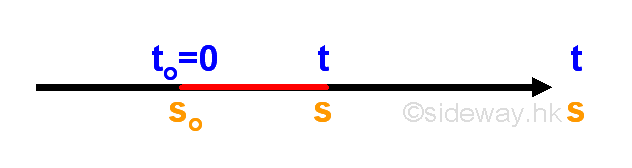
For a linear motion with uniform speed v, the relationship between the travelled distance s, initial distance so, speed v and time t can be expressed as a function: 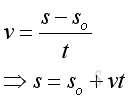
Instantaneous velocity can be defined as the instantaneous rate of change of the travelled distance with respect to the time of travelling. The derivative of the function s with respect to time t is. 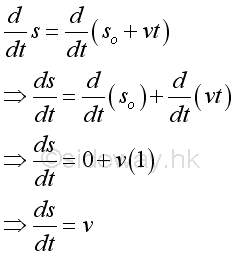
For a linear motion with constant acceleration a, the relationship between the final speed v, initial speed vo, acceleration a and time t can be expressed as a function: 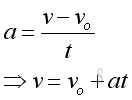
Instantaneous acceleration can be defined as the instantaneous rate of change of the travelling velocity with respect to the time of travelling. The derivative of the function v with respect to time t is. 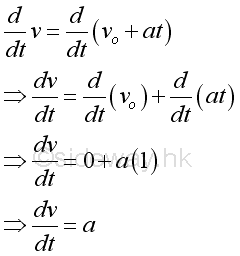
Since s is a function of time f(t), the derivative v is equal to the first derivative of function s with respect to t. 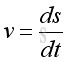
The derivative a is equal to the derivative of function v with respect to time t. But v is also a derivative of function s with respect to time t, the derivative is
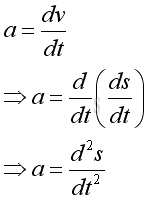
Therefore the derivative a is also equal to the second derivative of function s with respect to t. Linear Motion ProblemFor an object with a linear motion and the motion can be described by a distance function s with respect to time t. 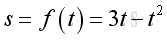
Graphically 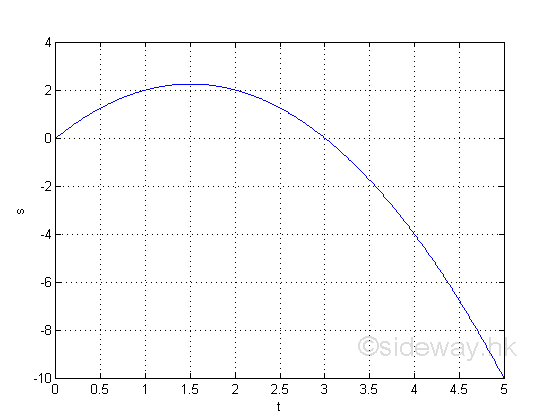
The information directly from the function is the travelled distance from the original location. e.g. at t=1, the distance from the original location is 2, 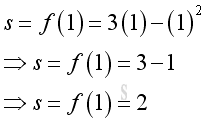
e.g. at t=2, the distance from the original location is 2 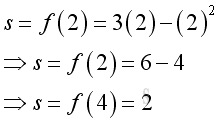
e.g. at t=4, the distance from the original location is -4, the negative sign means the distance is measured from the opposite side of the original location relative to the original default measurement. 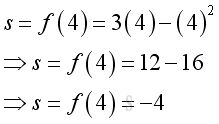
The first derivative can be used to determine the instantaneous verlocity of the object motion. imply 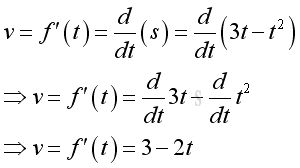
Graphically 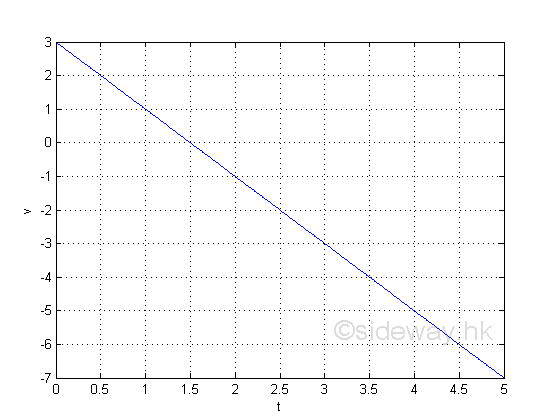
The information directly from the derivative is the instantaneous velocity. e.g. at t=1, the instantaneous velocity is 1 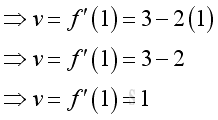
e.g. at t=2, the instantaneous velocity is -1, the negative sign means the direction of motion is opposite to the originial direction of the default motion. 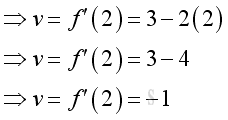
e.g. In stationary state condition, the instantaneous velocity of the object is eqaul to zero. Imply 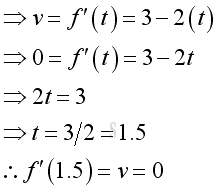
Therefore at t=1.5, the object remains stationary at its location with a zero instantaneous velocity. Imply the location is 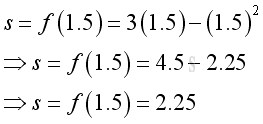
The second derivative can be used to determine the instantaneous acceleration of the object motion. imply 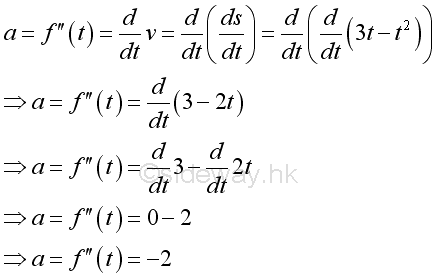
The accelation is equal to -2, a negative acceleration. The value is a negative constant which imply it is a constant deceleration. And therefore the instantaneous velocity is decreasing with respect to time. Graphically, the acceleration is 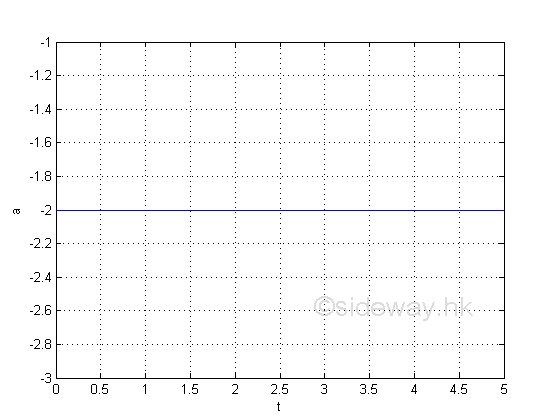
|
Sideway BICK Blog 21/09 |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||

