Sideway
BICK BLOG from Sideway
Sideway
BICK BLOG from Sideway
|
Link:http://output.to/sideway/default.asp?qno=110900015 Circular Motion Instantaneous Rate of ChangeIn linear motion, the instantaneous rate of change is related to the physical displacement of an object with respect to time. But the instantaneous rate of change can also be related to the travelled angular displacement or tangential distance of an rotating object with respect to the angle of rotation in radians or with respect to time. Circular Motion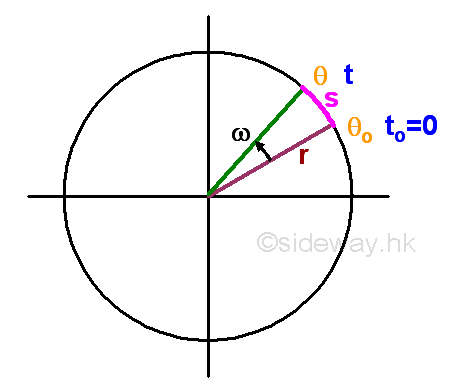
For a uniform circular motion, the object is moving in a circular path. When the object rotates from one position to another about the centre of rotation with radius r, the angle c measured in radians formed between the initial and final position of the object with the centre of rotation that the rotating object experiences is called the angular displacement or angular distance. For a circular motion with uniform angular speed ω, the relationship between the travelled angular distance θ, initial angular distance θo, angular speed ω and time t can be expressed as a function: 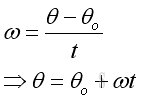
Instantaneous angular velocity can be defined as the instantaneous rate of change of the travelled angular distance with respect to the time of travelling. The derivative of the function θ with respect to time t is. 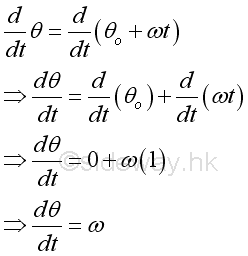
For a circular motion with constant angular acceleration α, the relationship between the final angular speed ω, initial angular speed ωo, angular acceleration α and time t can be expressed as a function: 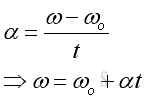
Instantaneous angular acceleration can be defined as the instantaneous rate of change of the travelling velocity with respect to the time of travelling. The derivative of the function ω with respect to time t is. 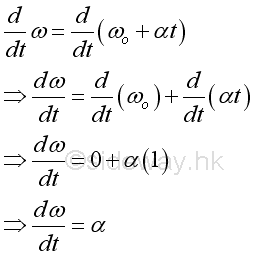
Since θ is a function of time f(t), the derivative ω is equal to the first derivative of function θ with respect to time t. 
The derivative α is equal to the derivative of function ω with respect to time t. But ω is also a derivative of function θ with respect to time t, the derivative is 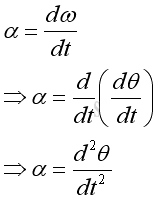
Therefore the derivative α is also equal to the second derivative of function θ with respect to time t. Rotational and Translational MotionAnd the travelled distance s or the angular distance is equal to the length of the angular path through which it moves along with. The relationship between the travelled distance s, radius r and angular displacement θ can be expressed as a function: 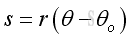
Since both the angular distance s and angular displacement θ are functions of time t, the instantaneous rate of change of the angular distance s with respect to time are also a function of the instantaneous rate of change of the angle θ of the angular displacement measured in radians. And they are related by the radius r of the circular motion. The derivative of the function s with respect to time t is. 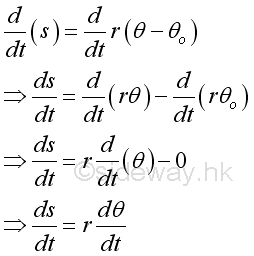
Therefore the instantaneous linear velocity is 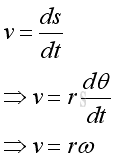
Since s is a function of time f(t), the derivative v is equal to the first derivative of function s with respect to t. 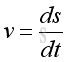
The derivative a is equal to the derivative of function v with respect to time t. But v is also a derivative of function s with respect to time t, the derivative is 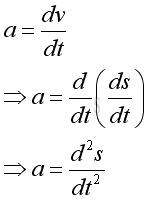
Therefore the derivative a is also equal to the second derivative of function s with respect to time t. Besides, the instantaneous linear acceleration can also be expressed in terms of angular displacement, imply 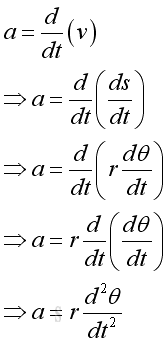
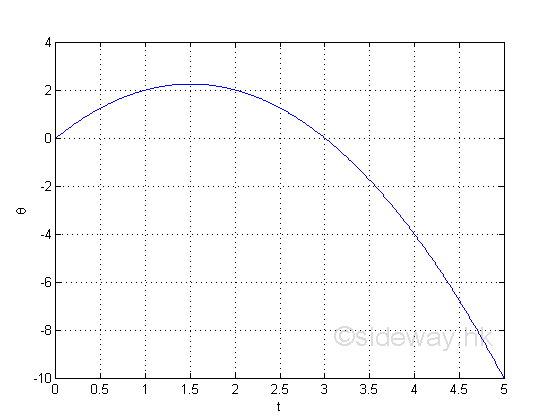
Circular Motion ProblemFor an object with a circular motion and the motion can be described by a function θ with respect to time t. 
Graphically
The information directly from the function is the travelled angular distance from the original position. e.g. at t=1, the angular distance from the original position is 2, 
e.g. at t=2, the angular distance from the original position is 2 
e.g. at t=4, the angular distance from the original position is -4, the negative sign means the angular distance is measured from the opposite direction of the original position relative to the original default measurement. 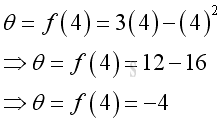
The first derivative can be used to determine the instantaneous angular verlocity of the object motion. imply 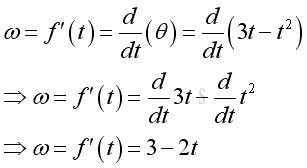
Graphically 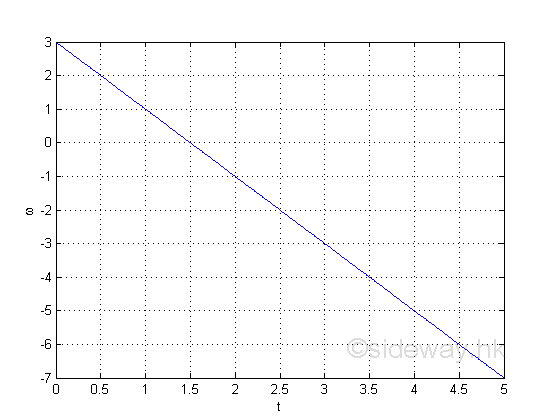
The information directly from the derivative is the instantaneous angular velocity. e.g. at t=1, the instantaneous angular velocity is 1 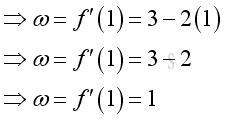
e.g. at t=2, the instantaneous velocity is -1, the negative sign means the direction of motion is opposite to the originial direction of the default motion. 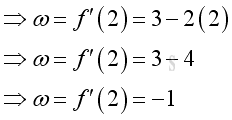
e.g. In stationary state condition, the instantaneous angular velocity of the object is eqaul to zero. Imply 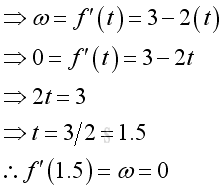
Therefore at t=1.5, the object remains stationary at its position with a zero instantaneous angular velocity. Imply the position is 
The second derivative can be used to determine the instantaneous angular acceleration of the object motion. imply 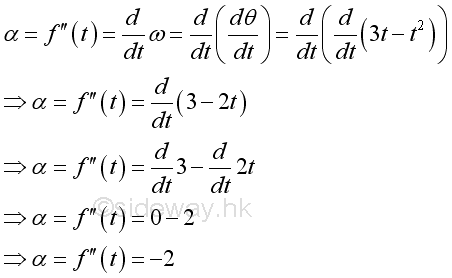
The angular accelation is equal to -2, a negative angular acceleration. The value is a negative constant which imply it is a constant deceleration. And therefore the instantaneous angular velocity is decreasing with respect to time. Graphically, the angular acceleration is 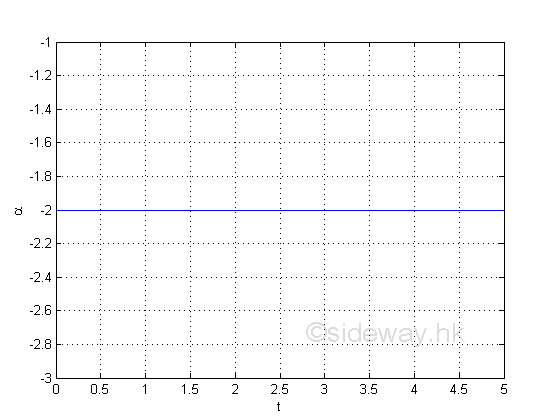
Link:http://output.to/sideway/default.asp?qno=110900016 Flow Rate Instantaneous Rate of ChangeIn linear or circular motion, the instantaneous rate of change is related to the physical displacement of an object with respect to time. But the instantaneous rate of change is also related to the the movement of some quantity passing through a reference with respect to time. Flow Rate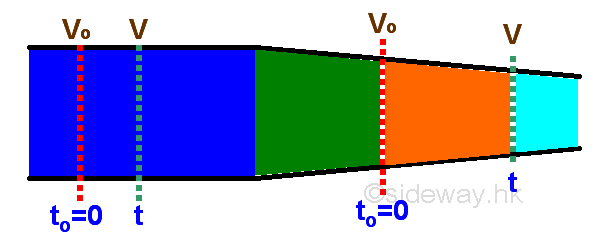
Flow rate usually refer to the volumetric flow rate of an object. Volume flow rate q is defined as the volume of the object passes through a given surface per unit time. When the given surface is equal to one unit, the velocity of the object flow is equal to the magnitude of the volume flow rate. For a steady flow, the relationship between the final volume V, initial volume Vo, volume flow rate Q and time t can be expressed as a function: 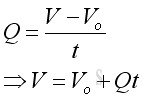
Instantaneous flow rate can be defined as the instantaneous rate of change of the volume flow through a reference with respect to the time t. The derivative of the function is.. 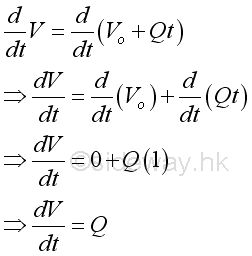
The volume flow rate is a constant for both a steady uniform flow and a steady nonuniform flow because the parameters of the flow do not change in time at every point. However only the uniform flow does have the parameters of the flow are the same for all spatial points along the flow, e.g. flowing through pipe with constant diameter. But for the nonuniform flow, the parameters of the flow vary and are different at different spatial points along the flow, e.g. flowing through a tapering pipe. For a steady flow with constant acceleration, the relationship between the final volume flow rate Q, initial volume flow rate Qo, acceleration a and time t can be expressed as a function: 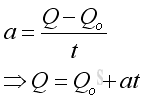
Instantaneous acceleration can be defined as the instantaneous rate of change of the volume flow rate with respect to the time. The derivative of the function is. 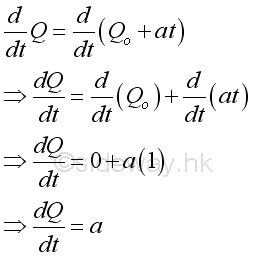
Since V is a function of time f(t), the derivative Q is equal to the first derivative of function V with respect to time t. 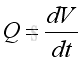
The derivative a is equal to the derivative of function Q with respect to t. But Q is also a function of time, the derivative is 
Therefore the derivative a is also equal to the second derivative of function V with respect to t. Flow Rate ProblemA water supply system is operated by a water pump. The water supply after switching on the pump can be described by a volume function V with respect to time t. 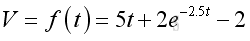
Graphically 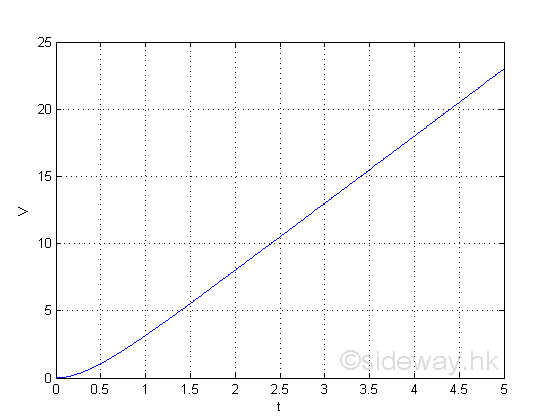
The information directly from the function is the total pumped water. e.g. at t=1, the total pumped water is 3.1, 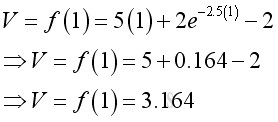
e.g. at t=2, the total pumped water is 8, 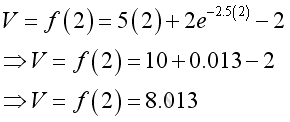
e.g. at t=3, the total pumped water is 13, 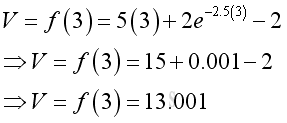
The first derivative can be used to determine the instantaneous volume flow rate. imply 
Graphically 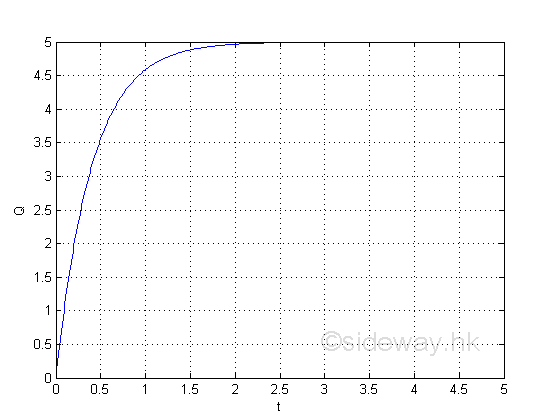
The information directly from the derivative is the instantaneous volume flow rate. e.g. at t=1, the instantaneous volume flow rate is 4.59 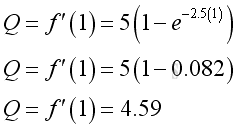
e.g. at t=2, the instantaneous volume flow rate is 4.97. 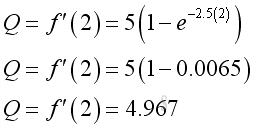
e.g. at t=3, the instantaneous volume flow rate is 5 
The second derivative can be used to determine the instantaneous acceleration of the instantaneous volume flow rate. imply 
Graphically 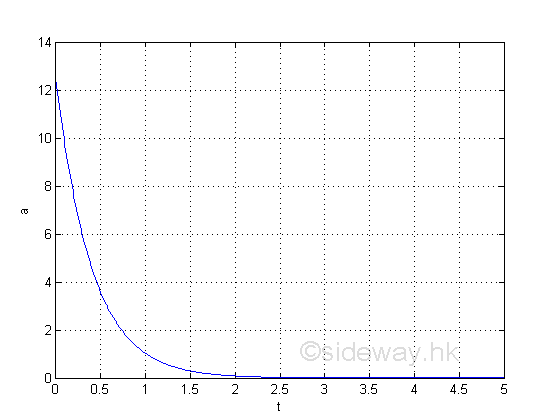
The information directly from the derivative is the instantaneous acceleration. e.g. at t=1, the instantaneous acceleration is 1.026 
e.g. at t=2, the instantaneous acceleration is 0.804 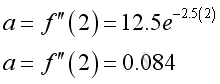
e.g. at t=3, the instantaneous acceleration is 0.007 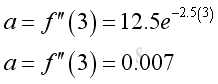
|
Sideway BICK Blog 22/09 |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||