Trigonometry

Those fundamental trigonometric identities are related with the properties of trigonometric functions. Some trigonometric  identities or Laws are derived as mathematical equalities that are always true for used with trigonometric functions simlificaton and transformation .

The Pythagorean identities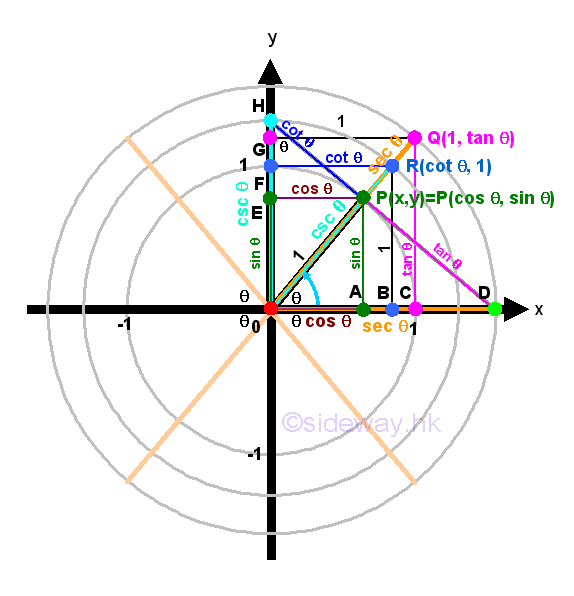

As the point P, lied on the unit circle, can be viewed as the leg of a right-angled triangle ΔPOA with hypotenuse equal to 1, the Pythagorean theroem can be applied, that is x2+y2=z2. Substituting x=cos(θ), y=sin(θ) and z=1 into the equation x2+y2=1. Imply (cos(θ))2+(sin(θ))2=1 and for convenience the identity is written as cos2(θ)+sin2(θ)=1. The identity implies the theorem is always true for any angle θ. Impy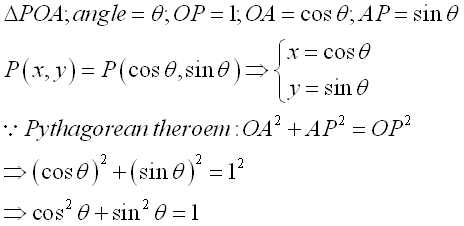

The identity can be used to determine the unknown term up to a sign, ±, when either the cos(θ) or sin(θ) is known. The ambiguity of the sign, ±, can be removed if the terminal side of angle θ lies on the coordinate system in standard position is known. Impy

Besides the most important pythagorean identity of sine and cosine functions, other pythagorean identities can also be obtained by Pythagorean theorem from other similar right-angled triangles ΔQOC and  ΔROB, that is 1+tan2(θ)=sec2(θ) and cot2(θ)+1=csc2(θ) . Imply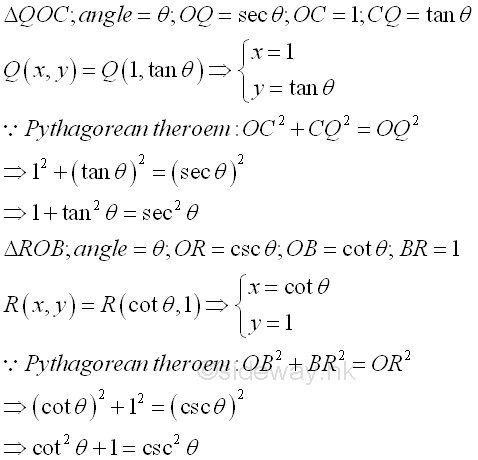

Or derived from the first pythagorean identity.  Impy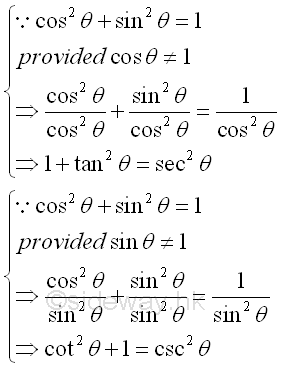

The Pythagorean Conjugates

Since Pythagorean identities are made up of squares, Pythagorean identities can also be transformed to other forms called the Pythagorean Conjugates by making use of Difference Of Squares. Through rearrangement of the Pythagorean identity to the form of difference of squares, a Pythagorean identity can then be factored into two factors accordingly. That is cos2(θ)+sin2(θ)=1 becomes 1-cos2(θ)=sin2(θ) or 1-sin2(θ)=cos2(θ), imply (1+cos θ)(1+cos θ)=sin2(θ) or (1+sin θ)(1+sin θ)=cos2(θ). And 1+tan2(θ)=sec2(θ) becomes sec2(θ)-tan2(θ)=1, imply  (sec θ+tan θ)(sec θ-tan θ)=1. And cot2(θ)+1=csc2(θ) becomes csc2(θ)-cot2(θ)=1, imply (csc θ+cot θ)(csc θ-cot θ)=1. These are the basic Pythagorean Conjugates only because these Pythagorean Conjugates can be easily tranformed another form by the multiplication or division of suitable trigonometric function accordingly, Imply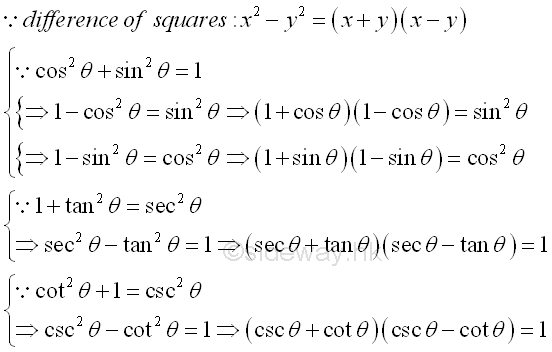

The Angles Sum and Difference Identities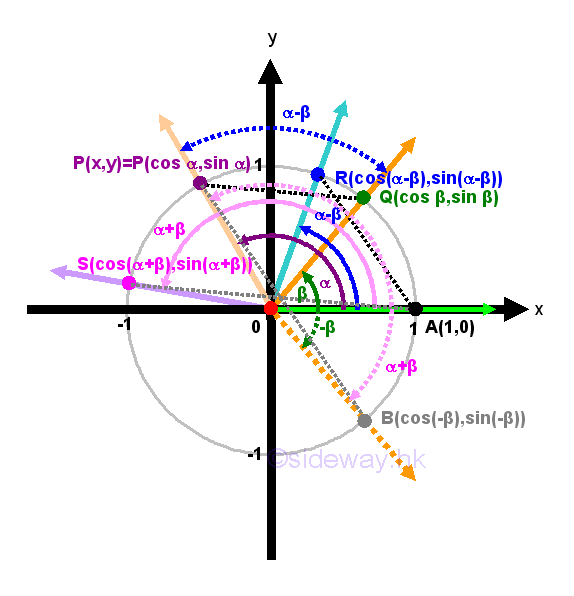

The angles sum and difference identities can be represented using the unit circle definition of trigonometric functions. Consider the angle difference identities in the Cartesian coordinate system. Let P, Q, R, and A be intersection points on unit circle where the coordinates of points are represented by the angles included by the terminal sides of the cooresponding angle. Let ∠POA be α and ∠QOA be β with α>β, then ∠POQ be equal α-β. Let ∠ROA be α-β. By SAS condition, ΔPOQ and ΔROA are congruent triangles, the lengths or distances of PQ and RA are equal. Equating the two lengths by distance formula or from Pythagorean theorem, then √((cos β-cos α)2+(sin β-sin α)2)=√((1-cos(α-β))2+(0-sin(α-β))2)
 ⇒(cos β-cos α)2+(sin β-sin α)2=(1-cos(α-β))2+(0-sin(α-β))2 
⇒(cos2β-2(cos β)(cos α)+cos2α)+(sin2β-2(sin β)(sin α)+sin2α)=(1-2cos(α-β)+cos2(α-β))+sin2(α-β). Simplified by Pythagorean identity, then 2-2(cos β)(cos α)-2(sin β)(sin α)=2-2cos(α-β) ⇒(cos α)(cos β)+(sin α)(sin β)=cos(α-β).  Since distance is used between two intersection points and the coordinate of a point is directly related with the terminal side of an angle, α and β can be any number provided α>β, for the case α<β, the identity still hold by applying the angle β-α to the argument of the identity, that is replacing α by β and β by α. Geometrically, ∠POB is equivalent to angle α+β, that is equal to α-(-β). Similarly, let ∠SOA be α+β. By SAS condition, ΔPOB and ΔSOA are congruent triangles, the lengths or distances of PB and SA are equal. Angle sum identity can than be obtained by equating the two lenghts by distance formula as before. Or by replacing angle β with angle (-β) directly and using negative angle indentities to simplify the equation. Imply
(cos(-β))(cos α)+(sin(-β))(sin α)=cos(α-(-β)) ⇒(cos(-β))(cos α)+(sin(-β))(sin α)=cos(α+β)   
⇒(cos β)(cos α)-(sin β)(sin α)=cos(α+β). Imply

The angles sum and difference identities for sine function can also be obtained by the another sets of angles sum and difference with respect to the positive y-axis instead of positive x-axis such that the distance between points are difference along with the cofunction identities. Imply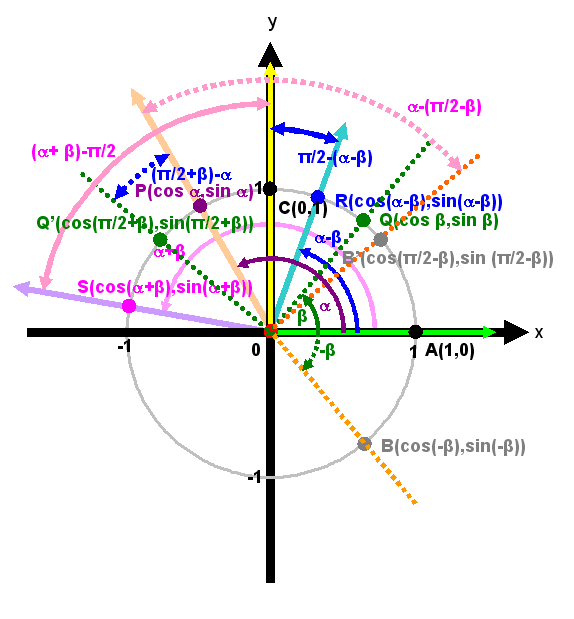

The paired distances to be considered are distances between points C and R and points P and Q', and distances between points C and S and points P and B'. The angles sum and difference identities for sine function can then be obtained through equating the two distance formulas similarly. Imply

Indeed, the angles sum and difference identities for sine function can be derived from the angles sum and difference identities for cosine function using the cofunction identities. Imply

Similarly, the angles sum and difference identities for tangent function can also be derived from the angles sum and difference identities for sine and cosine functions using the cofunction identities. Imply