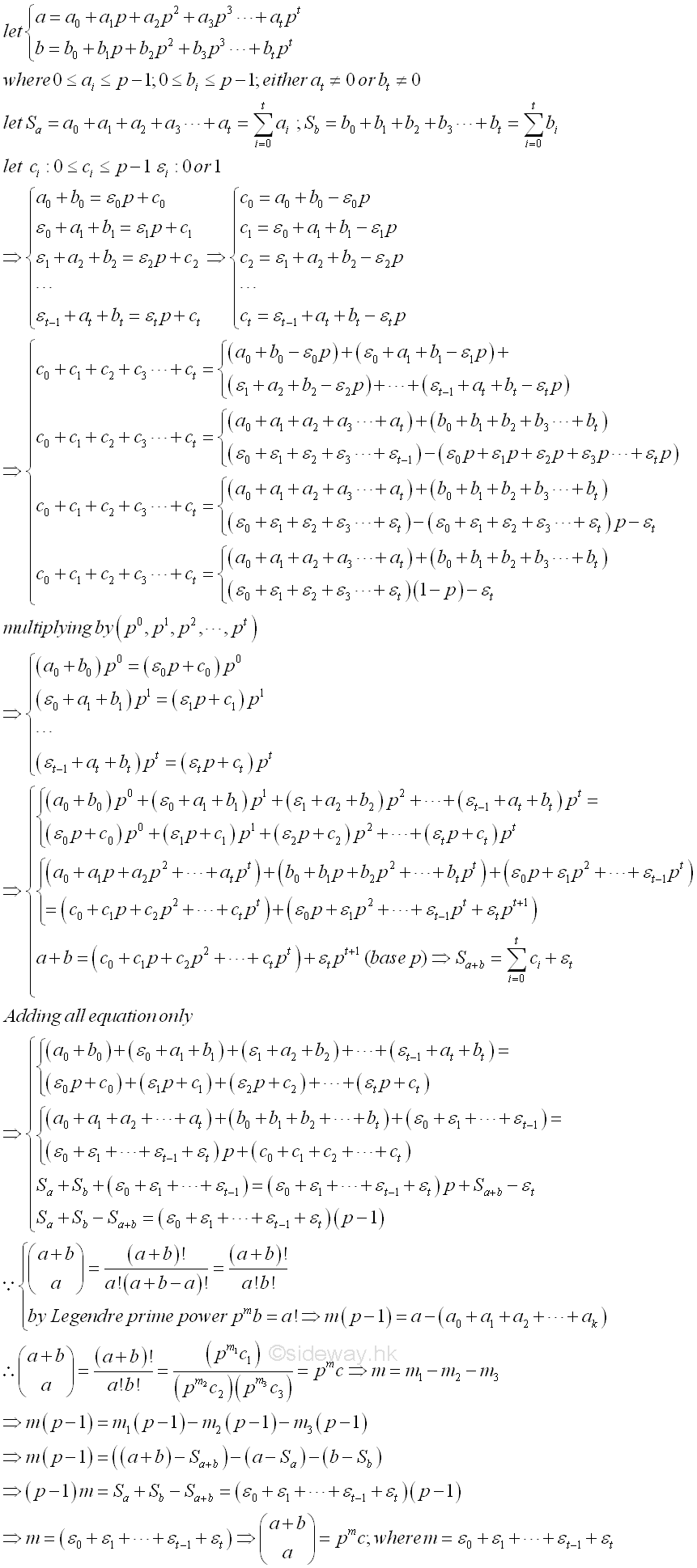Primality

Prime numbers are natural numbers, e.g. 2, 3, 5, 7,..., which can only be divided by 1 and itself. Although the way to recognize the primality of a natural numbe is very simple, there is difficulty of distinguishing prime numbers from composite numbers when natural numbers become very large.

The Porperty of Mann and Shanks (1972)[1,3]

Another property of prime related to binomial coeffiecent is the property of Mann and Shanks characterized by the divisibility of the binomial coefficients relatived to a prime number p in the specified manner. Instead of focusing on one individual set of binomial coefficients, Mann and Shanks checks the divisibility of multiple sets of the binomial coefficients relatived to a prime number p. In order to visualize the relationship, Mann and Shanks tabulate the Pascal's Arithmetical Triagle by shifting the starting column of each row two places to the right relative to the prievious row.  In other words, the row n of binomial coefficient with power index n  is placed between columns 2n and 3n inclusive. Column number p is a prime number if and only if row number k divides (k
p-2k) for every largest integer k such that  ⌊(p+2)/3⌋,  ⌊(p+2)/3⌋+1,...,⌊p/2⌋.

The binomial coefficients for each row in term of row number n is (n
i) where k=0,1,2,...n. Or in term of column number p is (p/2
i) where i=0,1,2,...p/2., since p/2=n. From the table, the only possible column p such that the whole column of the binomial coefficients are divisible by the first row number index is equal to n*2+n-1=p with binomial coefficient (n
n-1) or m*2+m-2=p with binomial coefficient (m
m-2) for n,m>2. In other words, the first row number is equal k=⌊(p+2)/3⌋ and the binomial coefficient is equal to (k
p-2k). Similarly, the possible whole column of the binomial coefficients are divisible by the last row number index is equal to n*2+1=p with binomial coefficient (n
1). In other words the last row number index n is equal to n=(p-1)/2 or k=⌊(p)/2⌋. the binomial coefficient is equal to (k
p-2k), Therefore the property can be specified as before.

For prime number p greater than 3, the row number index p can be expressed as p=6k+1=3n-2 or p=6k-1=3n-1. Consider p=6k+1=3n-2, imply n=2k+1 and the corresponding binomial coefficients in the column is (2k+i
3i-1). where the row index i=1,2,...,k. Since the two binomial coefficients of successive rows are (2k+m-1
3m-4), and (2k+m
3m-1) ), imply  (2k+m-1
3m-2)(2k+m)=(2k+m
3m-1)(3m-1). If row number 2k+m does not divide the binomial coefficient, then gcd(2k+m,3m-1)>1. Therefore gcd(6k+3m,3m-1)>1 , imply (6k+1,3m-1) or (p,3m-1)>1. In other words p is divisible and p is not a prime number. Therefore if p is a prime number, each binomial coefficients in the same column must be divisible by its row number. Similarly, if p=6k-1=3n-1, imply n=2k and the corresponding binomial coefficients in the column is (2k+i
3i+1). where the row index i=0,1,2,...,k-1. Since the two binomial coefficients of successive rows are (2k+m-1
3m-2), and (2k+m
3m+1) ), imply  (2k+m-1
3m)(2k+m)=(2k+m
3m+1)(3m+1). If row number 2k+m does not divide the binomial coefficient, then gcd(2k+m,3m+1)>1. Therefore gcd(6k+3m,3m+1)>1 , imply (6k-1,3m+1) or (p,3m+1)>1. In other words p is divisible by 3m+1 and p is not a prime number. Therefore if p is a prime number, each binomial coefficients in the same column must be divisible by its row number.

Since all even column number p have a non divisible binomial coefficients for  (p
0), all even column number p is not a prime. For all odd composite column number p=s(2t+1) where s is prime factor and t≥1. Let row number n=st where n does not divide the binomial coefficient at column p. The binomial coefficient at n row and p column is (st
s)=t(st-1
s-1) , therefore ther row number n=pk does not divide the binomial coefficient.

The Prime Power Dividing a Factorial (1808)[1]

In 1808, Legendre determined the exact prime power pm that divideds a factorial a! and m can also be expressed in terms of the p-adic development of a, that is  ((a-(a0+a1+a2+a3+...+ak))/(p-1). By definition a!=pmb, where p∤b. Let a>p, then a=q1p+r1 with 0≤q1, 0≤r1<p. Imply q1=⌊a/p⌋. For multiples of p not bigger than a, i.e. p,2p,...q1p≤a, then by definition, pq1(q1!)=pmc where p∤c as a is divided into q1 segments. Let m=q1+n1, then  pq1(q1!)=pq1+n1c or pn1 divides q1!. For each 1≤i≤k, there are ⌊q1/pi⌋-⌊q1/pi+1⌋ numbers between 1 and q1 is divided by the greatest power i of p only. So the greatest power of p dividing q1! is ∑ k
i=1 i(⌊q1/pi⌋-⌊q1/pi+1⌋)=∑ k
i=1 (⌊q1/pi⌋). Therefore n1 is equal to ⌊q1/p1⌋+⌊q1/p2⌋+.... Since ⌊q1/pi⌋=⌊⌊a/p⌋/pi⌋=⌊a/pi+1⌋, imply  n1=⌊a/p2⌋+⌊a/p3⌋+⌊a/p4⌋+.... From m=q1+n1, imply m=⌊a/p⌋+n1=⌊a/p1⌋+⌊a/p2⌋+⌊a/p3⌋+⌊a/p4⌋+....

Let a=akpk+...+a1p+a0. where pk≤a<pk+1 and 0≤ai≤p-1 for i=0,1,...,k.   Then ⌊a/p⌋=akpk-1+...+a2p+a1, ⌊a/p2⌋=akpk-2+...+a3p+a2, ..., ⌊a/pk⌋=ak, Therefore m=∑ k
i=1 (⌊q1/pi⌋) can be expressed as (akpk-1+...+a2p+a1)+(akpk-2+...+a3p+a2)+(akpk-3+...+a4p+a3)+...+(ak)=  a1+a2(p+1)+a3(p2+p+1)+...+(ak)(pk-1+pk-2+...+p+1)= ((a1(p-1)+a2(p2-1)+a3(p3-1)+...+ak(pk-1))/(p-1)=  ((a1p+a2p2+a3p3+...+akpk)-(a1+a2+a3+...+ak))/(p-1)= (a-(a0+a1+a2+a3+...+ak))/(p-1). and is equal to the p-adic valuation of a!

The Prime Power Dividing a Binomial Coefficient (1852)[1]

In 1852, Kummer extends the Legendre's result to determine the exact prime power pm that divideds a binomial coefficient  (a+b
a)=(a+b)!/a!b!, where a≥1,b≥1. Similar to Legendre, Let a=atpt+...+a1p+a0. and b=btpt+...+b1p+b0. where 0≤ai≤p-1 and 0≤bi≤p-1 for i=0,1,...,t. with either at≠0 or bt≠0. Let Sa=∑ t
i=0ai, Sb=∑ t
i=0bi be the sums of p-adic digits of a, b. Let ci be 0≤ci≤p-1 and εi=0 or 1. such that a0+b0=ε0p+c0, ε0+a1+b1=ε1p+c1,  ε1+a2+b2=ε2p+c2, ...,  εt-1+at+bt=εtp+ct. Therefore c0=a0+b0-ε0p, c1=ε0+a1+b1-ε1p,  c2=ε1+a2+b2-ε2p, ...,  ct=εt-1+at+bt-εtp. Or  (c0+c1+c2+...+ct)= ((a0+a1+a2+...+at)+(b0+b1+b2+...+bt))+(ε0+ε1+...+εt-1)-(ε0p+ε1p+ε2p+...+εtp)= ((a0+a1+a2+...+at)+(b0+b1+b2+...+bt))+(ε0+ε1+...+εt-1+εt)-(ε0p+ε1p+ε2p+...+εtp)-εt=  ((a0+a1+a2+...+at)+(b0+b1+b2+...+bt))+(ε0+ε1+...+εt-1+εt)(1-p)-εt.    By multiplying all equations with 1,p,p2,...pt .accordingly, imply a0+b0=ε0p+c0, (ε0+a1+b1)p=(ε1p+c1)p,  (ε1+a2+b2)p2=(ε2p+c2)p2, ..., (εt-1+at+bt)pt=(εtp+ct)pt.  After adding all equations together, imply a+b+(ε0p+ε1p2+...+εt-1pt)=(ε0p+ε1p2+...+εt-1pt+εtpt+1)+(c0+c1p+c2p2+...+ct-1pt-1+ctpt). Therefore a+b=(c0+c1p+c2p2+...+ct-1pt-1+ctpt+εtpt+1) and is equal to the expression of a+b in the base p. Similar to Sa, Sb, Sa+b=∑ t
i=0(ci)+εt. But when adding all equations only, then a0+b0+ε0+a1+b1+ε1+a2+b2+...+εt-1+at+bt=ε0p+c0 +ε1p+c1+ ε2p+c2+...+εtp+ct.  imply a0+a1+a2+...+at+b0+b1+b2+...+bt+ε0 +ε1 +...+εt-1=(ε0+ε1+ ε2+...+εt)p+c0+c1+c2+...+ct. Imply Sa+Sb+(ε0+ε1+...+εt-1)=(ε0+ε1+ ε2+...+εt)p+Sa+b-εt. Imply Sa+Sb-Sa+b=(ε0+ε1+ ε2+...+εt)(p-1). Since (a+b
a)=(a+b)!/a!(a+b-a)!=(a+b)!/a!b! , by Legendre prime power pmb=a!, m(p-1)=a-(a0+a1+a2+a3+...+ak), then (a+b)!/a!b!=(pm1c1)/((pm2c2)(pm3c3))=pmc , imply m=m1+m2+m3 , imply m(p-1)=((a+b)-Sa+b)-(a-Sa)-(b-Sb) . imply (p-1)m=(Sa+Sb-Sa+b)=(p-1)(`0+ε1+ ε2+...+εt) . Imply m=(`0+ε1+ ε2+...+εt). that is "The exact power of p dividing  (a+b
a) is equal to (`0+ε1+ ε2+...+εt), which is the number of 'carry-overs' when performing the addition of a, b, written in the base p. This theorem of Kummer was rediscovered by Lucas in 1878.