Trigonometry

Trigonometric functions are related with the properties of triangles. Some laws and formulas are also derived to tackle the problems related to triangles, not just right-angled triangles.

Area of Triangles Formulas

From geometry, area of triangles is equal to half of the product of the base and the height of a triangle. By trigonometry, the height of a triangle can always be expressed in term of sine function and one of its side except the side base. And the area of triangles formulas for two sides and the included angle is equal to the half of the product of the two sides times the sine function of the included angle. Although the area of triangles formula, (height)(base)/2 is proved geometrically, the trigonometric formulas of area of triangles can also be proved trigonometrically by applying the three cases as used in proving the law of sines with the help of geometry.

For the first case, an acute triangle ΔABC with angle-side opposite pairs (A,a), (B,b) and (C,c) and all the internal angles less than π/2, three altitudes from vertexes A, B, and C can be constructed to the side opposite of the acute triangle as the height of the considered orientation of the triangle accordingly.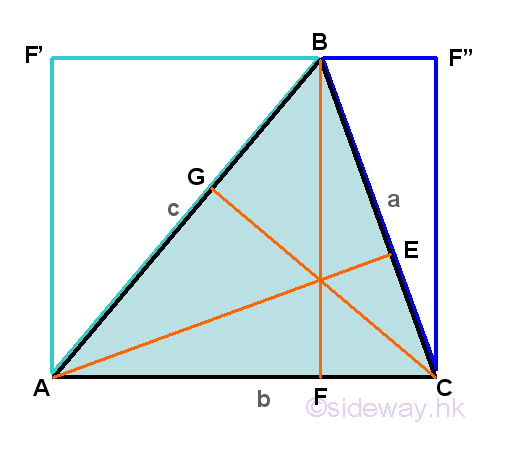

Each altitude can divide the triangle into two paired right-angled triangles with a common side accordingly in a similar way. Since the area of a right angled triangle is equal to half of the area of a rectangle formed by the height and base of the right angled triangle, the area of an acute triangle is equal to half of the product of the altitude and the base side. For example altitude BF , the area of triangle is ΔABC = ΔABF+ ΔCBF=(◻AF'BF)/2+(◻CF"BF)/2=(BF)(AF)/2+(BF)(FC)/2=(BF)(AF+FC)/2=(BF)(AC)/2. Since BF = c(sin A)=a(sin C), imply Area of ΔABC is ΔABC=(c(sin A))b/2=(a(sin C))b/2. Imply

For the second case, an obtuse triangle ΔABC with angle-side opposite pairs (A,a), (B,b) and (C,c) and one of the internal angles, A is greater than π/2 but less than π. Only one of the three altitudes which is drawn from vertex A can be constructed to the side opposite of the obtuse triangle, while the other two altitudes lie outside the obtuse triangle.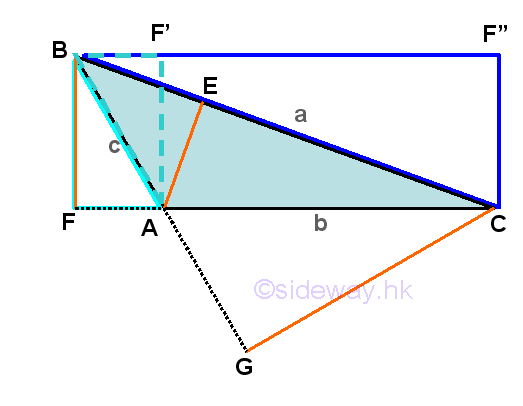

Similarly, ΔABC is divided by altitude AE to form two triangles  ΔABE and ΔACE as in the acute triangle case, two area of triangles formulas related to the altitude AE can be determined accordingly. Repeating the steps by considering another altitude, BF. Although ΔABC is not divided by altitude BF, the dropping of the altitude from vertix B also forms two new right-angled triangles,   ΔBAF and ΔBCF. Therefore the area of an obtuse triangle ΔABC is always equal to the area of right angled triangle ΔBCF minus the area of right angled triangle ΔBAF. Imply area of triangle ΔABC is ΔABC = ΔBCF- ΔBAF=(◻CF"BF)/2-(◻AF'BF)/2=(BF)(FC)/2-(BF)(AF)/2+=(BF)(FC-AF)/2=(BF)(AC)/2. Since BF = a(sin C)=c(sin(∠BAF)), and sin(∠BAF)=sin(π-∠BAC)=sin A, imply area of ΔABC is ΔABC=(a(sin C))b/2=(c(sin A))b/2. Imply

For the third case, a right-angled triangle ΔABC with angle-side opposite pairs (A,a), (B,b) and (C,c) and one of the internal angles, A is equal to π/2. Only one of the three altitudes which is drawn from vertex A can be constructed onto the side opposite of the right-angled triangle, while the other two altitudes lie on the sides of the right-angle triangle.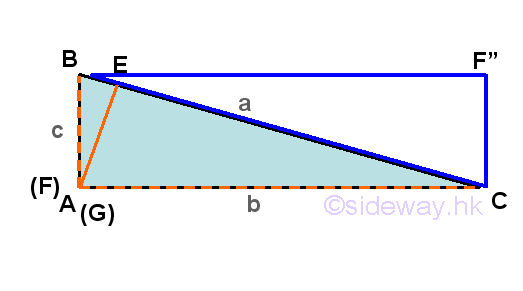

Similarly, ΔABC is divided by altitude AE to form two triangles  ΔABE and ΔACE as in the acute triangle case, two area of triangles formulas related to the altitude AE can be determined accordingly. For altitudes BF and CG, the two altitudes lie exactly on the side of the right-angled triangle, ΔABC. Since the area of an right-angled triangle ΔABC is always equal to the half of the area of the rectangle ◻CF"BF. Imply area of triangle ΔABC is ΔABC = ◻CF"BF)/2=(BF)(FC)/2=(AB)(AC)/2=cb/2. Since sin(∠BAF)=sin A=sin(π/2.)=1, imply ΔABC =cb/2=bc(sin A)/2,  Imply

Heron's Formula

The area of triangles formulas with two sides and the included angle can also be transformed to the form with three sides called Heron's formula using the law of cosines. Let s be the semiperimeter of the triangle and is equal to half of the sum of the three sides of the triangle. Then the area of triangle is equal to the square root of the product of four terms, the semiperimeter s, the difference of semiperimeter and side a s-a, the difference of semiperimeter and side b s-b, the difference of semiperimeter and side c s-c. That is √(s(s-a)(s-b)(s-c)). Imply

Proof Using Pythagorean Theorem

Pythagorean Theorem can also be used to prove the Heron's Formula instead of using the law of consines. And the area of triangles formula are used to simplify the proof in a general case. Imply

.