Trigonometry

Trigonometric functions are related with the properties of triangles. Some laws and formulas are also derived to tackle the problems related to triangles, not just right-angled triangles.

The Law of Cosines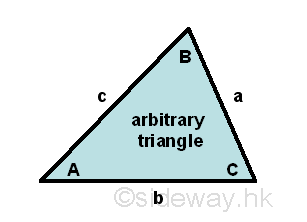

The law of cosines or cosine rule are related to the cosine functions of angles included in a triangle and the sides of the triangle. The Law of cosines states that for a given arbitrary triangle with angle-side opposite pairs (A,a), (B,b) and (C,c), the square of the side opposite to an angle is equal to the sum of the square of other two sides of the triangle including the angle minus the 2 times the product of the other two sides of the triangle times the cosine function of the included angle. Imply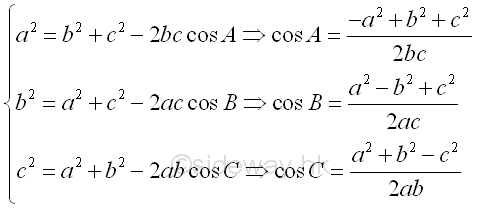

Similar to the law of sines, there are also three cases to be considered in proving the law of cosines for the three different types of angled triangles. The acute angled triangle with all the internal angles are less than π/2. The right angled triangle with one of the internal angles is equal to π/2. The obtuse angled triangle with one of the internal angles is greater than π/2 but less than π.

For the first case, an acute triangle ΔABC with angle-side opposite pairs (A,a), (B,b) and (C,c) and all the internal angles less than π/2, three altitudes from vertexes A, B, and C can be constructed to the side opposite of the acute triangle.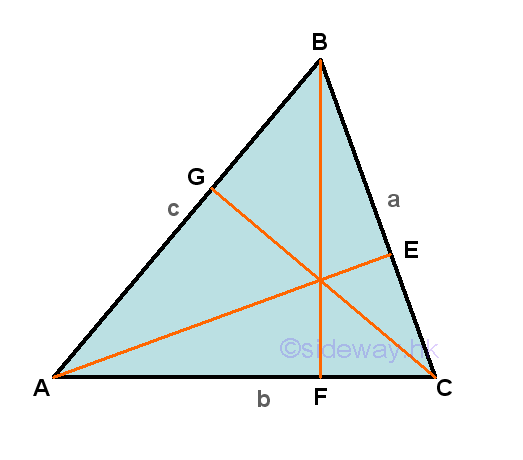

Each altitude can divide the side opposite to the vertex of the triangle into two parts accordingly to form two paired right-angled triangle in a similar way. For example, side b of ΔABC is divided by altitude BF drop from vertex B into AF and FC to form two triangles  ΔBAF and ΔBCF. According to the definition of cosine function, the line segment AF adjacent of angle ∠BAF will be the adjacent of the right angled triangle ΔBAF and the line segment FC adjacent of angle ∠BCF will be the adjacent of the right angled triangle ΔBCF respectively. That is cos A=AF/c and cos C=FC/a, imply AF=c(cos A) and FC=a(cos C), and therefore b=AC=AF+FC=c(cos A)+a(cos C). Repeating the steps by considering other two altitudes to get another two similar equations. That is c=AB=AG+GB=b(cos A)+a(cos B) and a=BC=BE+EC=c(cos B)+b(cos C). Equating three equations by multiplication and addition then a2=b2+c2-2bc(cos A), b2=a2+c2-2ac(cos B), and c2=a2+b2-2ab(cos C),. Imply

For the second case, an obtuse triangle ΔABC with angle-side opposite pairs (A,a), (B,b) and (C,c) and one of the internal angles, A is greater than π/2 but less than π. Only one of the three altitudes which is drawn from vertex A can be constructed onto the side opposite of the obtuse triangle, while the other two altitudes lie outside the obtuse triangle.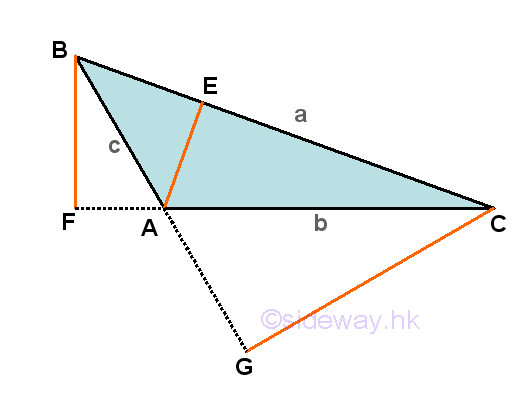

Similarly, ΔABC is divided by altitude AE to form two triangles  ΔABE and ΔACE.  According to the definition of cosine function, the line segment BE adjacent of angle ∠ABE will be the adjacent of the right angled triangle ΔABE and the line segment EC adjacent of angle ∠ACE will be the adjacent of the right angled triangle ΔACE respectively. That is cos B=BE/c and cos C=EC/b, imply BE=c(cos B) and EC=b(cos C), and therefore a=BC=BE+EC=c(cos B)+b(cos C). Repeating the steps by considering another altitude, BF. Although ΔABC is not divided by altitude BF, the dropping of the altitude from vertix B also forms two new right-angled triangles,   ΔBAF and ΔBCF. According to the definition of cosine function, the line segment AF adjacent of angle ∠BAF will be the adjacent of the right angled triangle ΔBAF and the line segment FC adjacent of angle ∠BCF will be the adjacent of the right angled triangle ΔBCF respectively. That is cos(∠BAF)=AF/c and cos C=FC/a, imply AF=c(cos(∠BAF)) and FC=a(cos C), and therefore b=AC=FC-AF=a(cos C)-c(cos(∠BAF)). Since ∠BAF=π-∠BAC==π-A, then cos(∠BAF)=cos(π-A), by reduction formula, cos(∠BAF)=-cos A. And therefore b=AC=FC-AF=a(cos C)+c(cos A) as before. Repeating the steps by considering the last altitude, CG. Although ΔABC is not divided by altitude CG, the dropping of the altitude from vertix C also forms two new right-angled triangles,   ΔCAG and ΔCBG. According to the definition of cosine function, the line segment AG adjacent of angle ∠CAG will be the adjacent of the right angled triangle ΔCAG and the line segment GB adjacent of angle ∠CBG will be the adjacent of the right angled triangle ΔCBG respectively. That is cos(∠CAG)=AG/b and cos B=GB/a, imply AG=b(cos(∠CAG)) and GB=a(cos B), and therefore c=AB=GB-AG=a(cos B)-b(cos(∠CAG)). Since ∠CAG=π-∠CAB=π-A, then cos(∠CAG)=cos(π-A), by reduction formula, cos(∠CAG)=-cos A. And therefore c=AB=GB-AG=a(cos B)-b(cos A) as before also. Equating three equations by multiplication and addition then a2=b2+c2-2bc(cos A), b2=a2+c2-2ac(cos B), and c2=a2+b2-2ab(cos C). Imply

For the third case, a right-angled triangle ΔABC with angle-side opposite pairs (A,a), (B,b) and (C,c) and one of the internal angles, A is equal to π/2. Only one of the three altitudes which is drawn from vertex A can be constructed onto the side opposite of the right-angled triangle, while the other two altitudes lie on the sides of the right-angle triangle.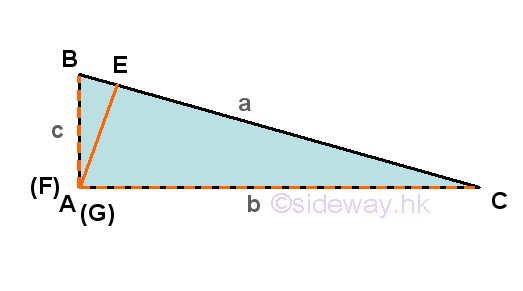

Similarly, ΔABC is divided by altitude AE to form two triangles  ΔABE and ΔACE.  According to the definition of cosine function, the line segment BE adjacent of angle ∠ABE will be the adjacent of the right angled triangle ΔABE and the line segment EC adjacent of angle ∠ACE will be the adjacent of the right angled triangle ΔACE respectively. That is cos B=BE/c and cos C=EC/b, imply BE=c(cos B) and EC=b(cos C), and therefore a=BC=BE+EC=c(cos B)+b(cos C). Repeating the steps by considering another altitude, for example BF. Although ΔABC is not divided by altitude BF, the dropping of the altitude from vertix B is exactly the side of the right-angled triangle,   ΔABC. According to the definition of cosine function, the cosine function of angle ∠BCA or cos C is cos C=b/a, imply b=a(cos C) and the cosine function of angle ∠ABC or cos B is cos B=c/a, imply c=a(cos B). Since cos A = cos π/2 is equal 0, therefore b=a(cos C)+c(cos A) and c=a(cos B)+b(cos A) as before also. Equating three equations by multiplication and addition then a2=b2+c2-2bc(cos A), b2=a2+c2-2ac(cos B), and c2=a2+b2-2ab(cos C). Imply

LibreOffice

LibreOffice is a software package for word processing, spreadsheets, presentations, database, and ... from libreoffice.org.

The graphic interface of LibreOffice from libreoffice.org: