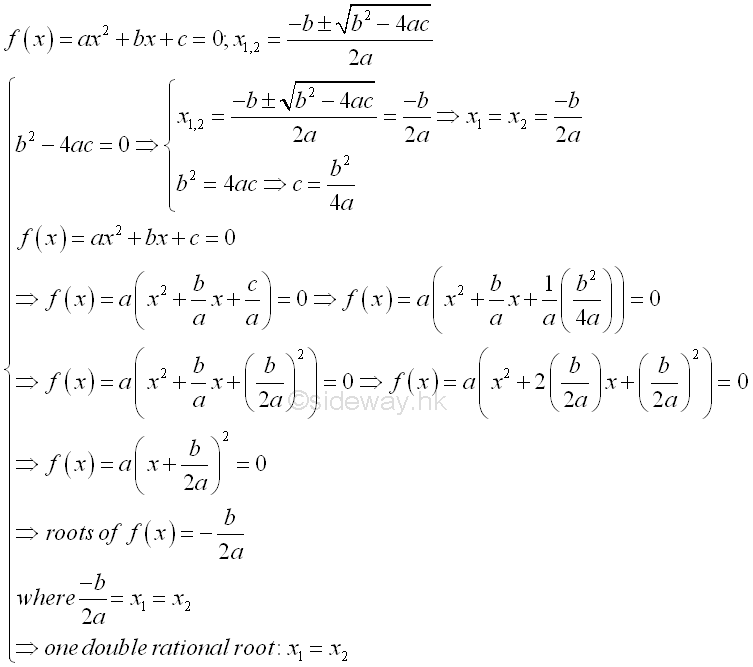Sideway
BICK BLOG from Sideway
Sideway
BICK BLOG from Sideway
|
Link:http://output.to/sideway/default.asp?qno=130500017 Quadratic Equations Quadratic EquationsA quadratic function is a polynomial function in a single variable, x, of the form equivalent to f(x)=ax2+bx+c with a≠0. The expression of a quadratic function is therefore called a polynimial of degree 2, or the second order or second degree polynomial with the highest exponent of the single variable, x equal to 2. And a quadratic equation is any equation of the form equivalent to ax2+bx+c=0 by setting the quadratic function equal to zero. Therefore a quadratic equation is only a typical example of a quadratic function. 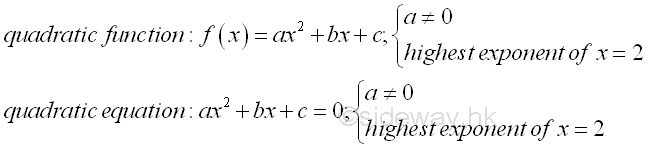
Roots of Quadratic Equations[1]The solutions of a quadratic equation is also called roots of a quadratic equation. Since a quadratic equation is a second order polynomial equation, a quadratic equation must has two solutions according to the fundamental theorem of algebra. In general, the solution may be both real, or both complex. Assume α and β are the roots of the quadratic equation, ax2+bx+c=0, the quadratic equation can then be written as (x-α)(x-β)=ax2-(α+β)x+αβ=0, imply (α+β)=-b/a and αβ=c/a by equating the coefficients of two polynomials. 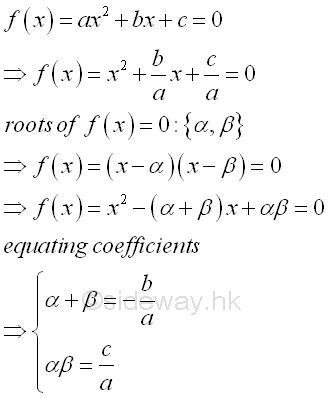
Quadratic Formula of Quadratic Equations[1]Analytically, the solutions of quadratic equation can be found by the method of "completing the square". The idea of determining the roots of a quadratic equation is making use of the symmetry of the quadratic function g(x) about a vertical axis parallel to the y-axis by transforming the quadratic equation f(x)=0 into a symmetry quadratic function g(x). The obtained formula for calculating the roots of the quadratic equation is called the quadratic formula. Imply 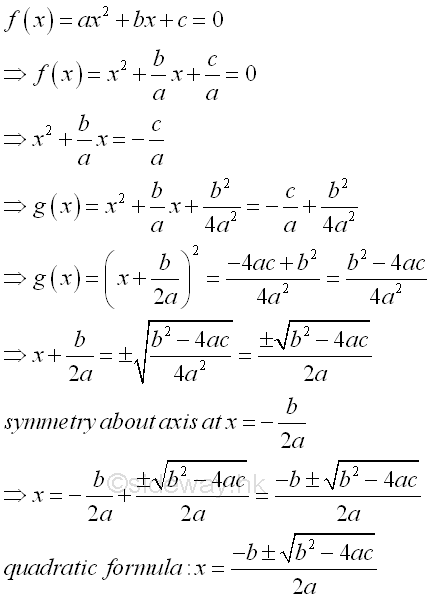
Assuming α≥β then the values of the α and β are 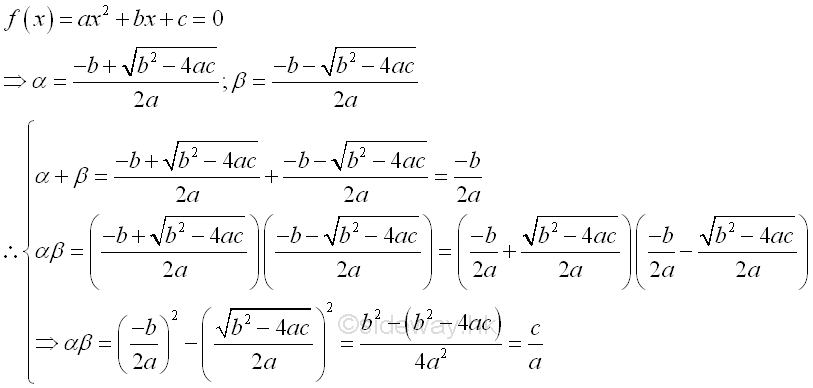
Discriminant of Quadratic Equations[1]According to the quadratic formula, the roots of a quadratic equation is charactered by the square root components of the quadratic formula. Depending on the value of expression (b2-4ac), the roots of a quadratic equation can be coincident, rational, real or complex numbers. And (b2-4ac) is therefore called the discriminant of the quadratic equation. In general, the discriminant, b2-4ac, can have four cases:
Alternate Form of Quadratic FormulaThe quadratic equation is obtained by setting the quadratic function equal to zero and x is not equal to zero, the quadratic formula can be derived in an alternative way. 
Forms of Quadratic FunctionThe quadratic function f(x)=ax2+bx+c is usually called the standard form of a quadratic function. Since a quadratic equation has two roots, the standard form of a quadratic function can be expressed in terms of the two roots, f(x)=a(x-x1)(x-x2), called factored form. 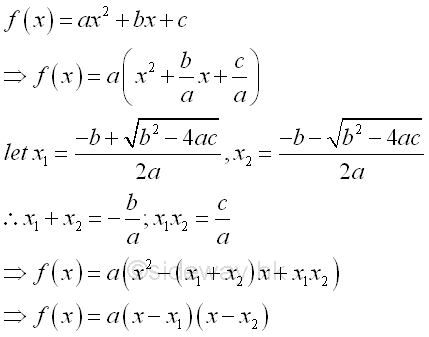
Besides the quadratic function is symmetric about a line, the standard form of a quadratic function can be expressed in terms of the vertex of the function, f(x)=a(x-x0)2+y0, called vertex form. 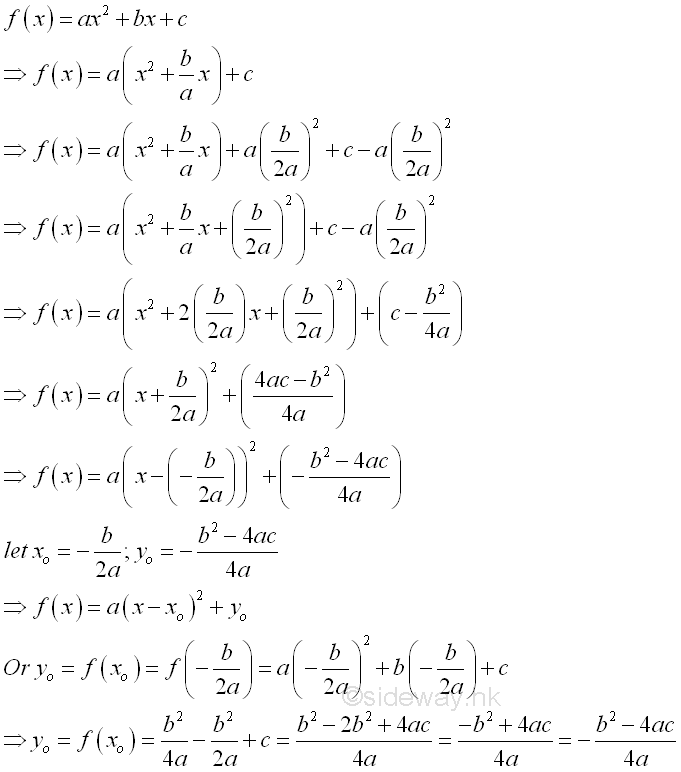
Sign of Quadratic Expression[1]Let E be the quadratic expression of the quadratic function f(x)=ax2+bx+c. If α and β are the roots of quadratic equation ax2+bx+c=0 and α≥β, then the sign of the quadratic expression can also be determined accordingly. In general, assuming the quadratic expression with two distinct real roots, when a is positive, E is positive if x>α or x<β and E is negative if α>x>β. Or when a is negative, E is positive if α>x>β and E is negative if x>α or x<β. In other words, E has same sign as coefficient a for x>α or x<β, and E has opposite sign as coefficient a for α>x>β. This case can also be considered as the case b2-4ac>0 with two distinct real root for the corresponding quadratic equation. Imply 
In the case b2-4ac=0 with double real root for the corresponding quadratic equation, this is a special condition of the general case where α equal to β and therefore the condition α>x>β becomes α=x=β is equal to zero. E has the same sign as the coefficient a. 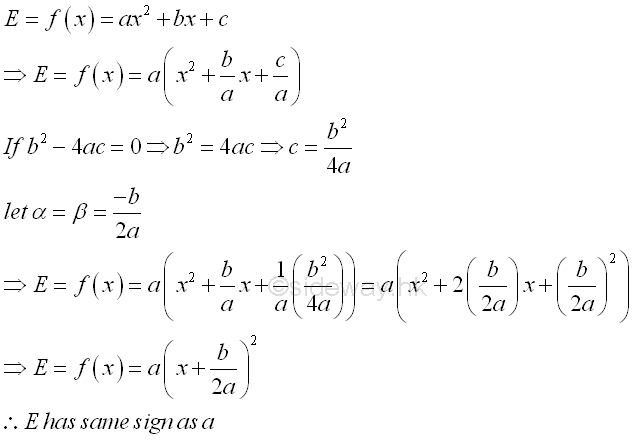
In the case b2-4ac<0 with two distinct complex root for the corresponding quadratic equation, this is a special condition of the general case where quadratic expression, E, does not equal to zero for all real x. E has the same sign as the coefficient a.. 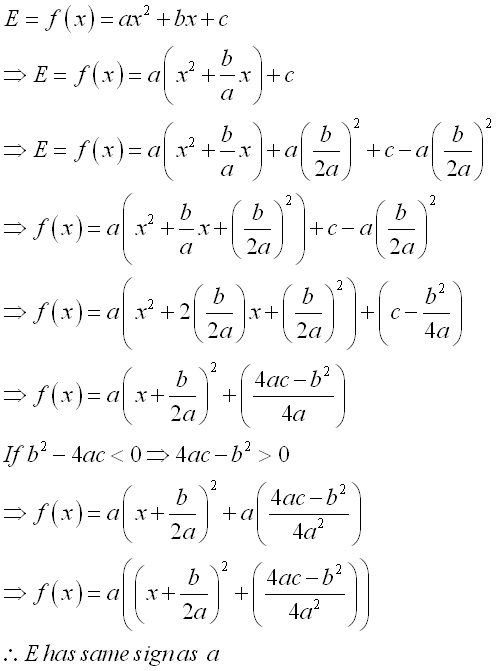
|
Sideway BICK Blog 16/05 |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||