 Sideway
BICK BLOG from Sideway
Sideway
BICK BLOG from Sideway
|
Link:http://output.to/sideway/default.asp?qno=130700030 Parametric Equation Parametric EquationSince a function f is defined as the one-to-one relationship between the input variable and the defined one-to-one permissible output variable, and therefore a function f can be expressed as y=f(x) where x is the input variable and y is the defined one-to-one permissible output variable. Or the inverse function 𝑔 can be expressed as x=𝑔(y) where y is the input variable and x is the defined one-to-one permissible output variable. Graphically, equations of these two forms of functions can be plotted as a curve on the Cartesian plane. However, not all curves or equations can be classified easily into these two forms of functions. For example, the motion of a particle moving on the xy plane can be described by a curve with coordinate (x,y) in the form of x=f(t) and y=𝑔(t) where t as the variable time is known as the parameter of the two equations. These two equations used as one set of equations to represent the curve is called the parametric equation of the curve or the parametric form of representation of a curve and the coordinate (x,y) is a function of one variable, t called parameter. 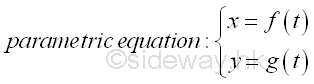
Derivative of Equation of Parametric formDot notation, or Newton's notation is usually adopted to denote the derivative of parametric equations. Imply 
Derivative of Cartesian Equation from Parametric formIn order to obtain the derivative of the Cartesian form of a curve from the parametric equation, the parameter t should be eliminated from the parametric equations between the value of x and y of the curve. However the derivative of Cartesian equation from parametric form can also be obtained from the parametric equations by making use of the rule of function of a function. Imply 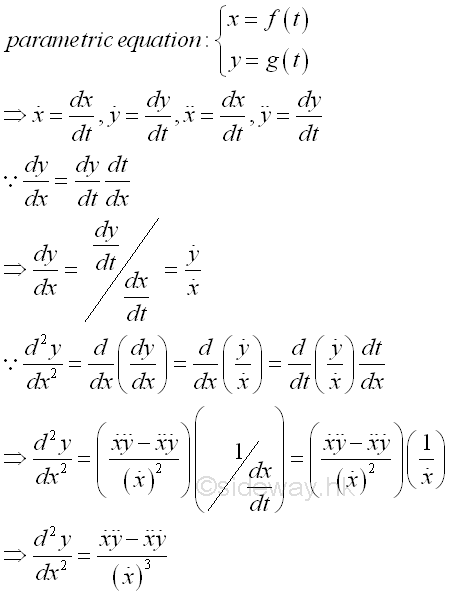
|
Sideway BICK Blog 16/07 |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||

