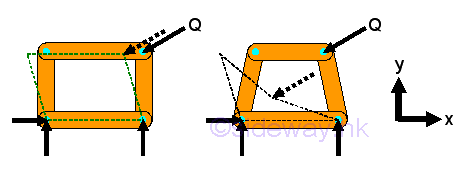
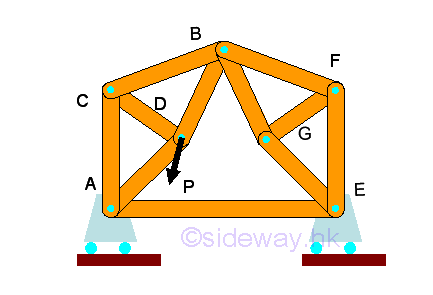
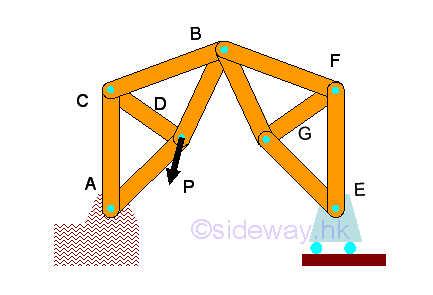
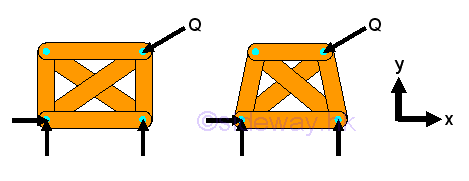
Space Truss

A space truss is also constructed with straight members connectede at connecting joints by hinged connection located at the two ends of each member to form a three dimensional structure in space. No member in the truss is continuous through a joint. A ball and socket jointing type connection is used for connecting truss members together at the connecting joint to allow free rotational motion for each truss member so that no moment or torsional resistance is transmitted through the connecting joint. Therefore, truss member in the truss behaves like a short link and only tensile and compressive force can be transferred between the end joints in static equilibrium. But in practical applications, truss members are usually joined together by means of bolted or welded connections.

Although the original joint design of a truss is a fictionless ball and socket connection, truss member can also be rigidly connected because there is little impact of the force flow in a completely constrained and kinematically determinate structure. Since when designing a truss, the axial stiffness of the truss members is already sufficiently large enough to maintain the structure in the stable working condition and to ensure the bending restraint required at the connecting joint is negligible also. Since no couple is applied to the truss members and forces can only be applied at the joints of a member, a truss member is a two-force member.

Simple Space Truss:

Stability:

The triangular configuration of truss members forms a rigid structure. A rigid coplanar truss can then be obtained by adding two truss members to the triangular structure. Similarly a rigid three  dimensional configuration can be obtained by adding three truss members to the triangular structure to form the tetrahedral configuration of a simple elementary rigid space truss.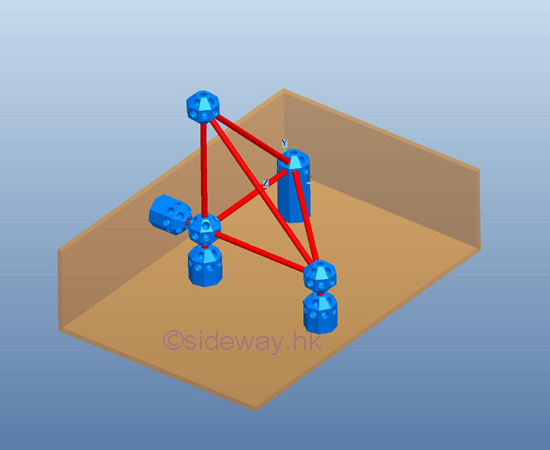

A simple space truss can then be constructed by adding three truss members to the exising joints of the basic simple rigid space truss and the other ends of the three truss members are connected together by a ball and socket jointing type connection to form a new joint which should not lie on the planar space formed by the joining joints, or the four connecting joints lie in a plane.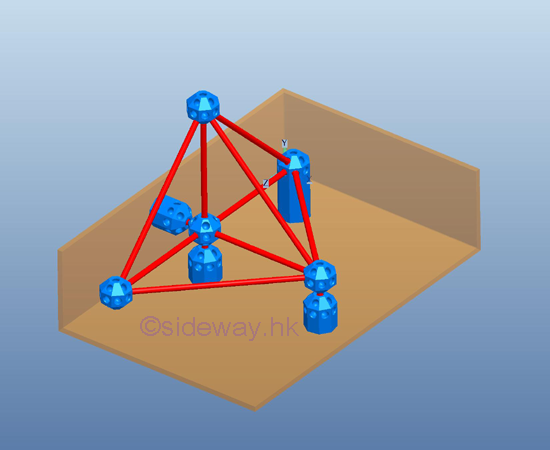

In general, a rigid space truss can be constructed by starting with a basic tetrahedral truss with six members and four joints. Therefore, for constructing a rigid space truss, three more members and one more joint are added to the rigid space truss. Mathematically, the total number of member m is equal to 3 times the total number of joints minus 6, i.e. m=3n-6. In other words,  the structure of a simple rigid space truss alway have the equation equal to m=3n-6.

Determinacy:

Since all truss members are two force member, each member has only one unknown force. The total number of unknown force is equal to the total number of truss member, M. Assume the total number of  unknown reactions in a three dimensional structure is R. Therefore the number of unknowns for a constrained truss is equal to number of truss members, M plus number of reactions, R, i.e.  total number of unknowns = M+R.

At each joint, there is no couple and three equilibrium equations of rectangular componenets can be formulated only. Therefore the number of equilibrium equations for a truss with number of joint N is 3 times the number of joints. i.e. total number of equilibrium equations = 3 N.

Although there are six more equilibrium equations can be written from the free body diagram of space truss since the truss is in static equilibrium, these six equilibrium equations are not independent equation. These static equilibrium equations can only provide additional relationship between external forces.

A space truss is statically determinate, only when the number of unknowns is equal to the number of equilibrium equations, i.e. M+R=3N. For a three dimensional completely constrained structure, the total number of reactions, R is equal to 6. The equation can be rewritten as M+6=2N or M=2N-6, which is same as the stability requirement, m=3n-6. Therefore a stable space truss is statically determinate only if the truss is properly constructured.

When additional member is added to a stable space truss, the space truss becomes over rigid and is statically indeterminate.

Forces Analysis:

For a completely constrained space truss, the total reactions provided by the supports and connections should be equal to six so that all the unknown reactions of the space truss is statically determinate. The supports and connections can be any combination of ball supports, roller supports and ball and socket connections. The six unknown reactions can be detemined by the six equilibrium equations from the free body diagram of the space truss.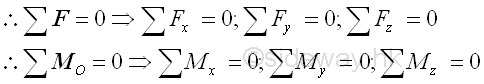

Since the connecting joint is in equilibrium and no couple is applied to the connecting join, three equilibrium equations of rectangular componenets can be formulated only. And therefore the method of joints can be used to determine the three unknown forces of joints with three connecting truss members.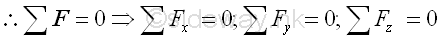

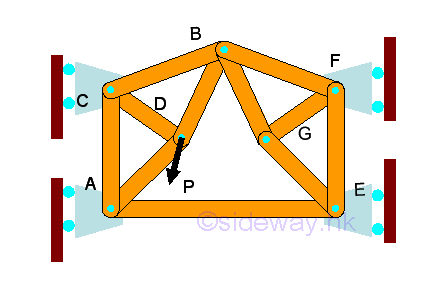
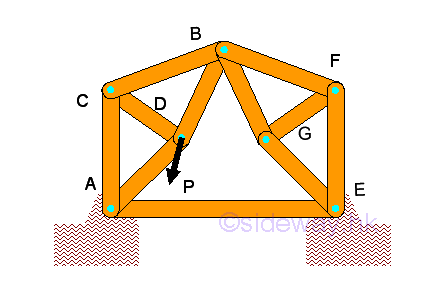
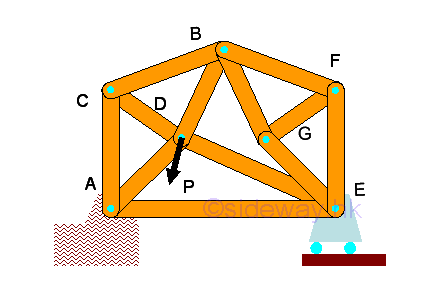
The method of sections can also be used to determine forces in the truss member. Since six equilibrium equations can be obtained from the free body  doagram of the sectional part of a space truss,  six unknown forces of truss member can be determined by the method of sections.

Planar Truss

Summary of stability and determinacy of planar truss: