 Sideway
BICK BLOG from Sideway
Sideway
BICK BLOG from Sideway
|
Link:http://output.to/sideway/default.asp?qno=120400011 Factorization FactorizationFactorization is one of the methods to verify whether a number is prime. Prime Factorization Trial DivisionThe direct search factorization is a bruce force factorization method for determining all possible prime factors of a composite number, N, through the repeated examination of divisibility by trial division from a set of non-trivial prime divisors. Let x, y are non-trivial factors of integer N with N=xy. imply 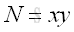
It is not necessary to test all numbers from 1 to N-1. If x, y are non-trivial factors of integer N with N=xy and x≤y, then x≤√N. Since if x>√N, then y≥x>√N and imply xy>N, which contradicts to the assumption N=xy. Therefore, the trial division can be performed by checking whether x divides N, x|N, for x=2 to the floor of √N. if x is found, imply x≡0 (mod N), and y, y=N/x is a factor also. In verifying whether a number N is prime, x can be limited to a non-trivial prime factor. Fermat FactorizationThe Fermat factorization (1600s) from Pierre de Fermat is another way of factoring a composite number by considering the composite number as the difference of squares. This standard binomial can then be factorized into a product. Imply 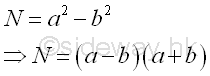
Since all even number can be divided by 2, let x, y are non-trivial odd factors of integer N with N=xy. imply 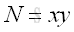
Equate two equations. Imply 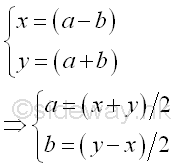
Both a and b are integers because x and y are odd integers, the sum and difference between any two odd number are even number which is divisible by 2. As x and y are non trivial factors, √N≥x>1 and y≥x, imply a≥1 and b≥0. Instead of testing the non trivial factors x, and y, Fermat factorization examine the integers a and b. Imply 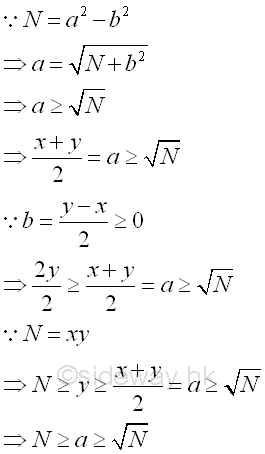
Therefore, the Fermat factorization can be performed by checking a from the floor of √N to N. whether the corresponding value of b is an integer and the corresponding terms of the product, (a-b) and (a+y) are the non trivial factors of N. Imply 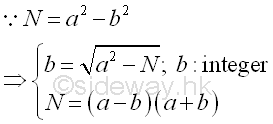
In verifying whether a number N is prime, the value of integer a should be choosen from the floor of √N to N. Pollard Rho FactorizationThe Pollard rho factorization or Pollard's Monte Carlo factorization method (1975) from J.M. Pollard is another technique of finding factors of a composite number by making use of probabilistic ideas from transforming a sequencial sequence to a congruential pseudo-random sequence to increase the probability of getting prime factors of the composite number. |
Sideway BICK Blog 17/04 |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||

