 Sideway
BICK BLOG from Sideway
Sideway
BICK BLOG from Sideway
|
Link:http://output.to/sideway/default.asp?qno=111100005 Bounded Area between Curves Bounded Area by FunctionsBounded area under a function or bounded area under a curve is the signed area between the curve and the axis over the closed interval [a,b]. In general, the net signed area of the curve bounded by the curve of function f(x) and the x-axis over the closed interval [a,b] by definite integral is 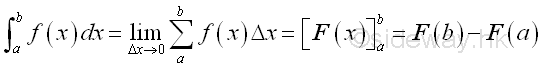
The net signed bounded area is the summation of all positive and negative infinitesimal elements. And therefore for problems of calculating the total bounded area of a function or concerning with the sign of the infinitesimal elements, the shape of the curve should be determined before applying the method of integration. 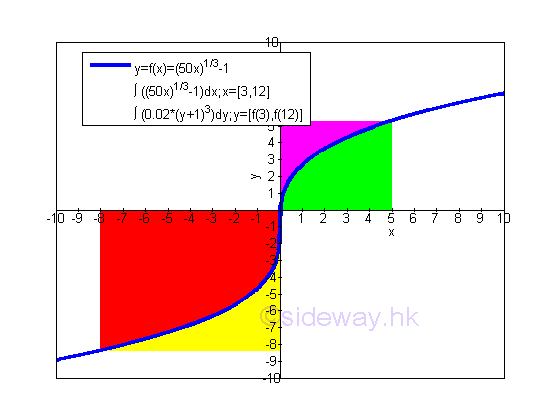
Depending on the arrangement of a function on the graph, there are two appraoches to calculate the bounded area between the curve and the axis. For bounded areas relatived to x axis, the bounded areas can be summed horzontally. For bounded areas relatived to y axis, the bounded areas can be summed vertically. Bounded Area between CurvesUnlike the concept of bounded area under curve, the bounded area by the curves of functions should always be positive and is equal to the total bounded area by curves of functions over the closed interval [a,b]. In order to obtain a positive area, the bounded area is always obtained by the function with larger value minus the function with smaller value. Therefore the shape of curves over the closed interval [a,b] should also be determined in order to identify all bounded areas before applying the method of integration. 
In general, when summing the infinitesimal area elements horizontally, the bounded area should be determined by the upper function minus the lower function within the region. 
And when summing the infinitesimal area elements vertically, the bounded area should be determined by the right function minus the left function within the region. 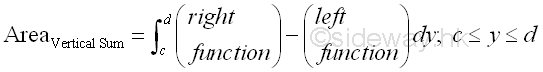
Bounded Area between curves by Horizontal Approach or Vertical Approach:Since the bounded area is bounded by curves of function, in some cases, the bounded area between curves can be obtained by either the horizontal sum or vertical sum approaches. For example, the two curves of two monotonically increasing functions f(x) and h(x) forms two seperated regions of bounded area within a closed interval. 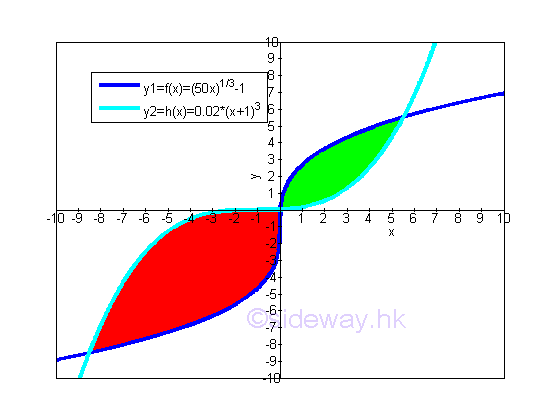
The closed intervals of the two regions of bounded areas are equal to the intersections of curves. imply 
The total bounded area between curves obtained by the horizontal sum approach is equal to the sum of the two regions of bounded areas. Imply 
Since the bounded area is bounded by the two curves of two monotonically increasing functions f(x) and h(x), the total bounded area of the two seperated regions of bounded area within a closed interval can also be obtained by the vertical sum approach. The transformation of the two functions is 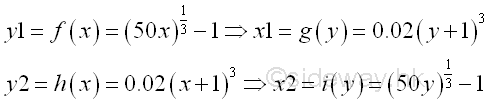
The bounded areas bounded by the two curves of two monotonically increasing functions g(x) and i(x) is 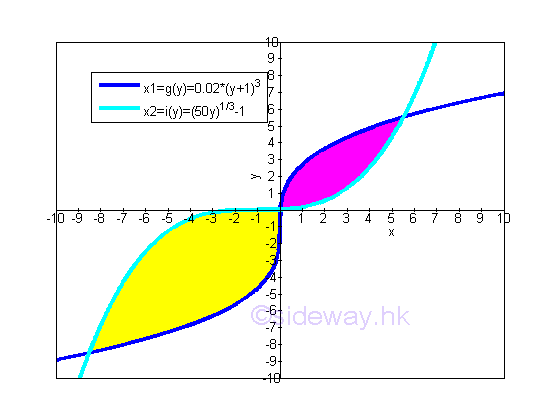
The total bounded area between curves obtained by the vertical sum approach is equal to the sum of the two regions of bounded areas. Imply 
The total bounded area between curves obtained by the vertical sum approach is equal to the total bounded area between curves obtained by the horizontal sum approach. Because of the summing method is changed from horizontal to vertical, the larger function in horizontal approach is also changed to the larger function in vertical approach accordingly. And therefore the larger function is highly depending on the domain and range used in the integration process. Bounded Area between curves by Horizontal Approach:In most cases, the approach used to obtaining total bounded area between curves is limited by the shapes of curves and the bounding curves. For example, if the range in x domain is changed to [-6,0.0213], the total bounded area of the curves of functions f(x) and h(x) on the closed interval [-6,0.0213] becomes. 
The easiest way to calculate the bounded area between curves is the horizontal sum approach. imply 
Bounded Area between curves by Vertical Approach:And in some cases, an additional curve, e.g. y>=-6 can be used as additional constrain with the range in x domain, e.g. [-8.5262,0.0213]. The total bounded area of the curves of functions f(x), h(x) and f(x)>=-6 on the closed interval [-8.5262,0.0213] becomes. 
Since y should be greater or equal to -6, the bounded area in x domain and y domain is 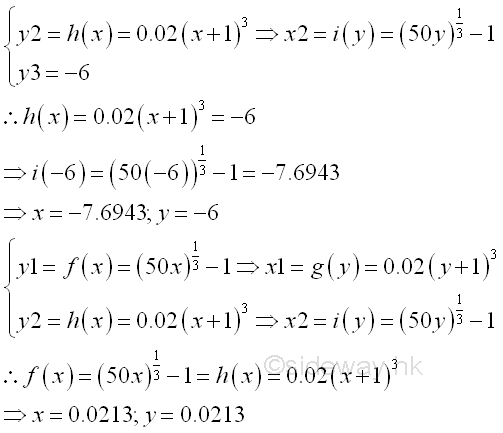
The easiest way to calculate the bounded area between curves is the vertical sum approach. imply 
Bounded Area between curves by Horizontal and Vertical Approaches:But in some cases, when an additional curve, e.g. y>=-6 is used as additional constrain with a shorter range in x domain, e.g. [-6,0.0213]. the total bounded area of the curves of functions f(x), h(x) and f(x)>=-6 on the closed interval [-6,0.0213] becomes. 
One way to calculate the bounded area between curves is using a vertical sum approach minus a horizontal sum approach. imply 
Similarly the bounded area between curves can also be obtained by a horizontal sum approach minus a vertical sum approach. Another way to calculate the bounded area between curves is using horizontal sum approach only by dividing the bounded area into two regions of bounded areas. The intervals of two regions are 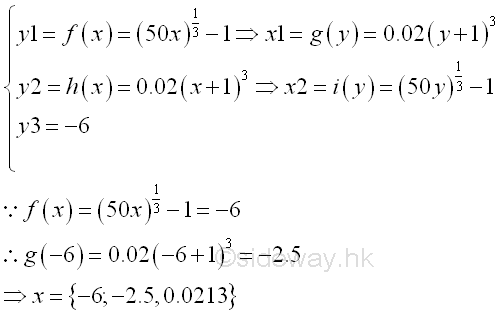
Therefore the bounded area between curves can also be obtained by adding two region of horizontal sum approach. Imply 
Similarly the bounded area between curves can also be obtained by adding two region of vertical sum approach. Link:http://output.to/sideway/default.asp?qno=111100004 Bounded Area under Curve Bounded Area of a FunctionDefinite integral can be interpreted as the net signed area of the curve bounded by the curve of function f(x) and the x-axis on the closed interval [a,b]. 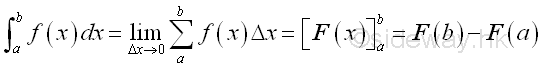
Since Δx is always positive, each infinitesimal element of area will have the same sign as the value of function f(x). The infinitesimal element of area can be positive, negative or zero. The infinitesimal element of area is called the signed area under the curve because the positive area is under the curve and the negative area is above the curve. Therefore the summation of all infinitesimal elements is the net signed bounded area. And for problems of calculating the total bounded area of a function or concerning with the sign of the infinitesimal elements, the shape of the curve should be determined before applying the method of integration. Bounded Area of a Curve which is entirely above the x-axisWhen the curve of a function f(x) is entirely above the x-axis, the area obtained by integration is positive and all infinitesimal elements are under the curve. 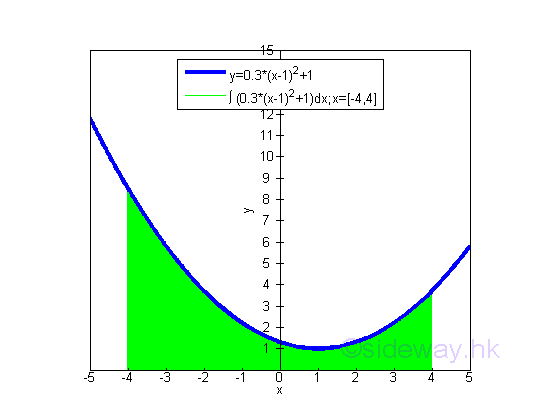
The bounded area underneath the curve of function y=0.3(x-1)2+1 between the closed interval -4 and 4 and above the x-axis is 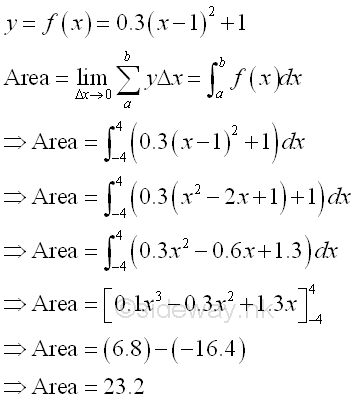
The bounded area under the curve and above the x-axis is positive and is equal to 23.2. But the integral of a function can be positive, negative or zero. Bounded Area of a Curve which is entirely below the x-axisWhen the curve of a function f(x) is entirely below the x-axis, the area obtained by integration is negative and all infinitesimal elements are above the curve. 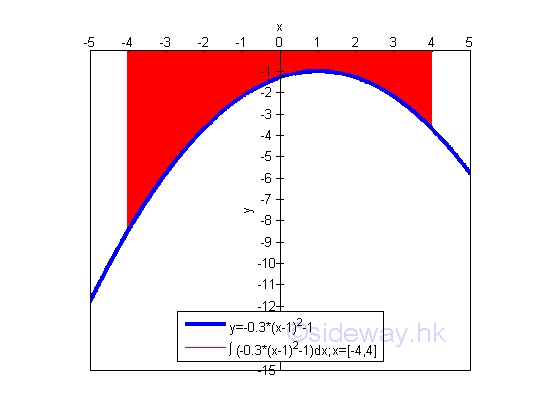
The bounded area above the curve of function y=-0.3(x-1)2-1 between the closed interval -4 and 4 and below x-axis is 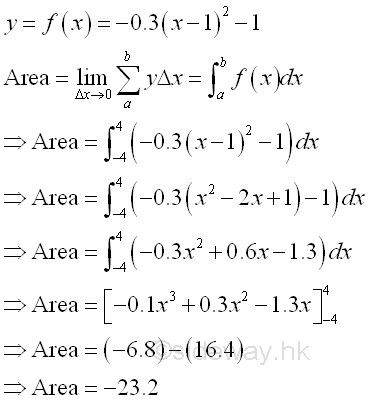
The bounded area above the curve and below the x-axis is negative and is equal to -23.2. The area is the absolute value of the signed area. But the integral of a function can be positive, negative or zero. Bounded Area of a Curve which is partly above and partly below the x-axisWhen the curve of a function f(x) is partly above and partly below the x-axis, the area obtained by integration is the net signed bounded area because the infinitesimal elements can be under or above the curve. 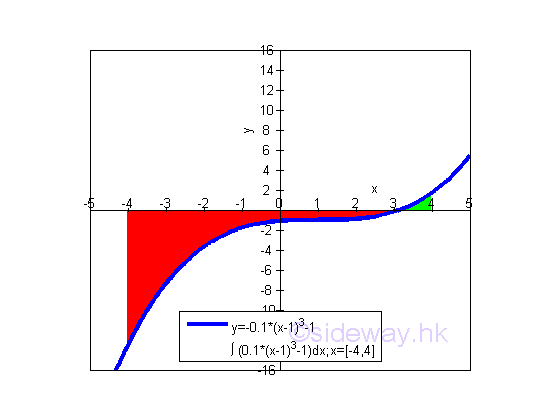
Net Bounded Area of a function:The net bounded area under the curve of function y=0.1(x-1)3-1 between the closed interval -4 and 4 of x axis is 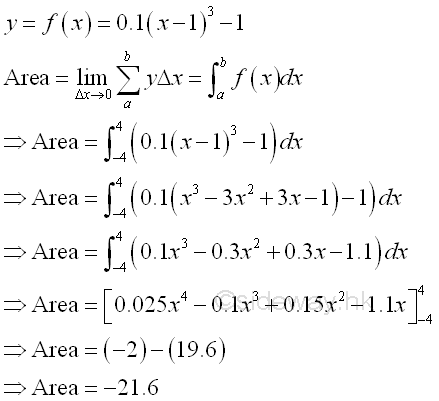
The net bounded area bounded by the curve and the x-axis is negative and is equal to -21.6. The area is the absolute value of the signed area. But the integral of a function can be positive, negative or zero. Total Bounded Area of a function:In order to calculate the total bounded area, the shape of the function f(x) should be determined first. The x-intersect of f(x) when y=0 is equal to 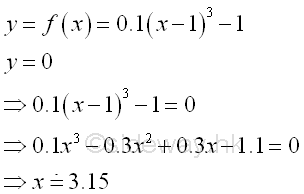
The bounded area bounded by the curve and below the x-axis is 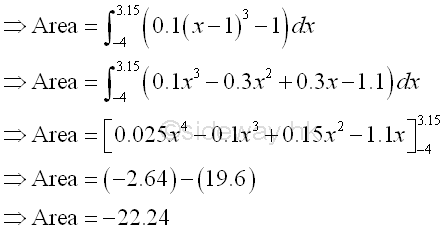
The bounded area bounded by the curve and above the x-axis is 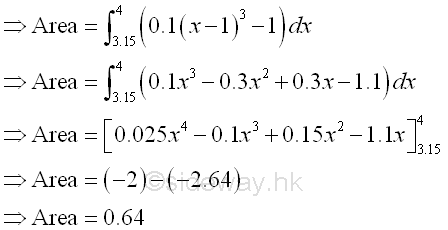
Therefore the net bounded area bounded by the curve is -22.24+0.64=-21.6 as before and the total bounded area bounded by the curve is the sum of absolute area, i.e. 22.24+0.64=22.88 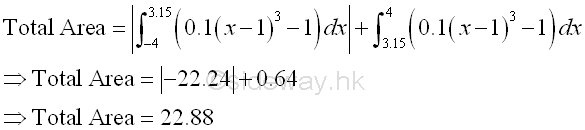
Bounded Area of a Curve through transformationSince finding the bounded area involving the finding of integral, sometimes finding the bounded area of a curve is much easier to sum vertically than to sum horizontally, that is using an easier way of finding the integral. And mathematically, the relationship between the bounded area by horizontal summation and the bounded area by vertical summation is 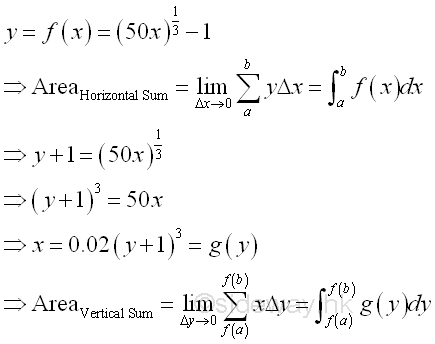
There is only a direct relationship between function f(x) and function g(x). And there is no direct relatonship between the horizontally summed area and the vertically summed area. In order to simplify the task of finding the integral, a transformation of the bounded area calculation is needed. The bounded area transformation can be carried out by integration by parts through the transformation of variable of integration. 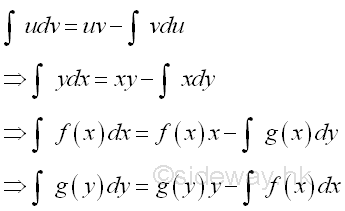
Geometrical Representation of Integration by Parts:Through variable of integration transformation, the formula of integration by parts can be used for the transformation of bounded area summation. In the formulas of integration by parts above, the x is obtained from dx through integration or the y is obtained from dy through integration. The practical forms of integration by parts are 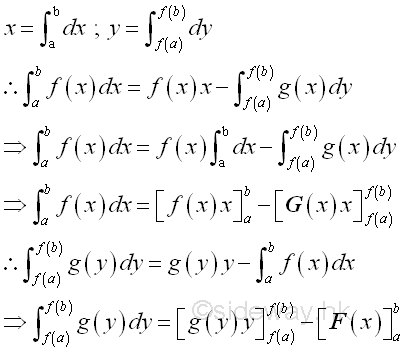
The first integral on the right hand side of the two integration by parts formulas above are equal because they are both derived from xy, 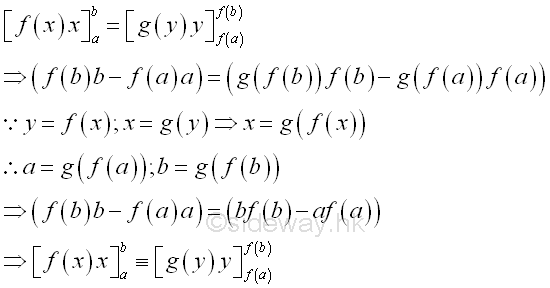
Therefore the term xy in the formula of integration by parts is equal to the product of the upper limits of x and y minus the product of the lower limits of x and y. Geometrically, the relationship between the bounded area by horizontal summation and the bounded area by vertical summation is 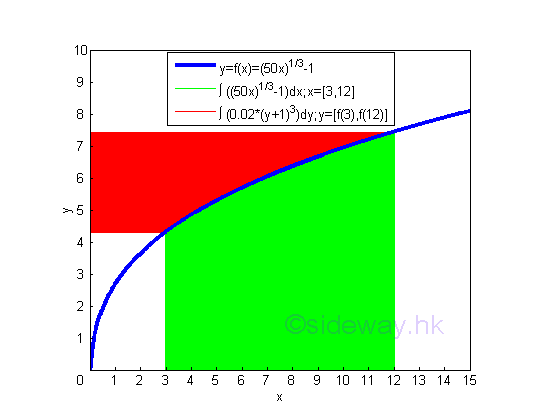
According to the graph, the sum of bounded red area and bounded green area is equal to the rectangular area formed by the upper limits (12,f(12)) and the origin (0,0) minus the rectangular area formed by the lower limits (3,f(3)) and the origin (0,0). The bounded green area by horizontal summation is 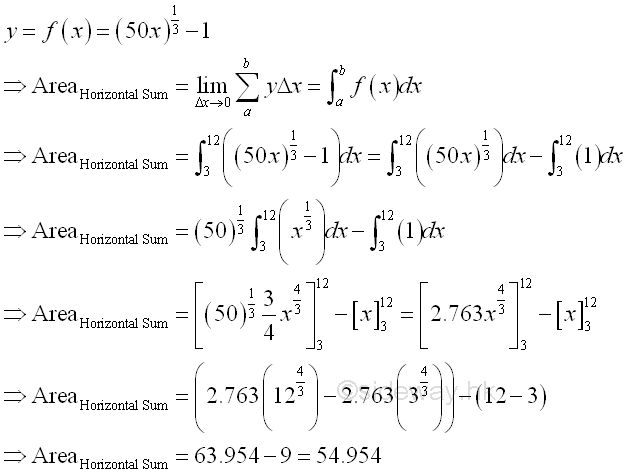
The bounded red area by vertical summation is 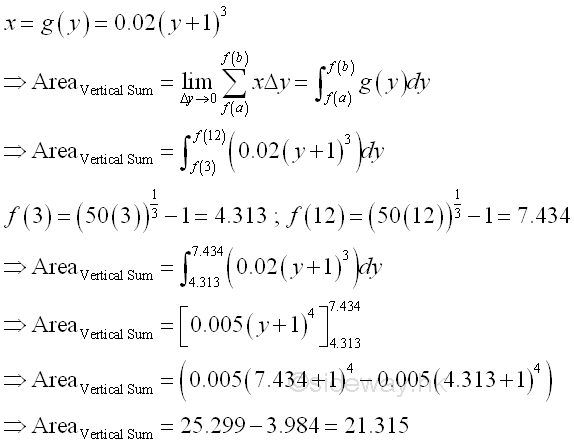
And the area formed by the two rectangular areas is 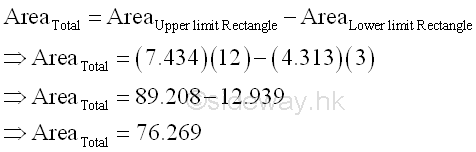
Therefore the term xy in the formula of integration by parts can be considered as the net total area of the net area of vertical sum plus the net area of horizontal sum, imply. 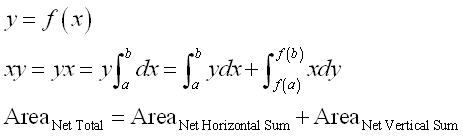
|
Sideway BICK Blog 21/11 |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||

