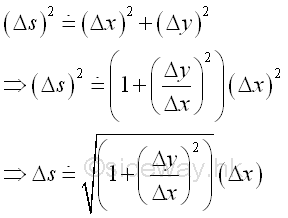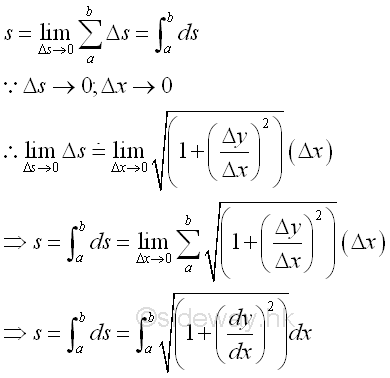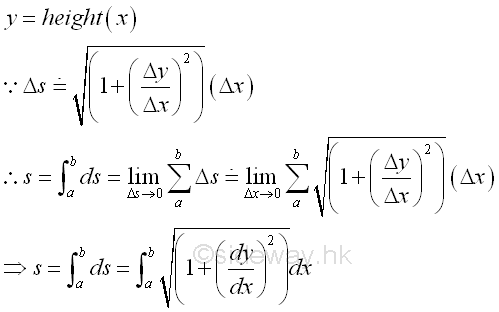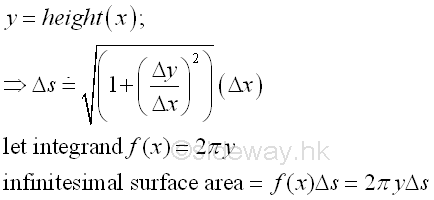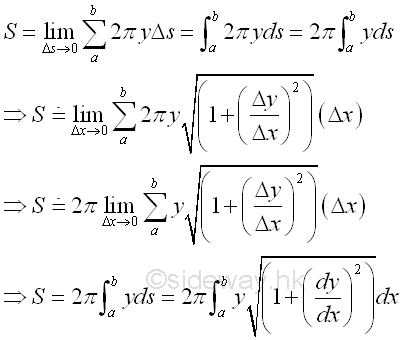Sideway
BICK BLOG from Sideway
Sideway
BICK BLOG from Sideway
|
Link:http://output.to/sideway/default.asp?qno=111100002 Interpretation Interpretations of IntegralSimilar to the interpretation of a derivative, the interpretations of integral can also be evaluated geometrically, physically, and approximately. But the varieties of interpretations on integral arise from the liaison of the mathematical model represented by the integrals to real life applications. For an integratable function f(x), the definition of integral of function F(x) is: 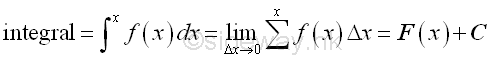
Unlike derivative, there are two types of integrals, definite and indefinite integrals and they are used for two different catalogs of applications.. Definite integral:The definite integral is the integral defined within upper and lower limits, and the definition of definite integral is 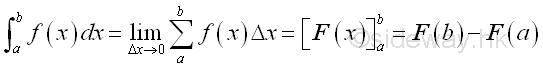
Therefore the definite integral is usually for the applications of determine the total effect of the function f(x) with respect to x over a closed interval [a,b]. Indefinite integral:The indefinite integral is the integral defined without limits, and the definition of definite integral is 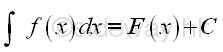
The indefinite integral is also called the anti-derivative because there is a close relationship between the integral and the derivative. And the relationship is 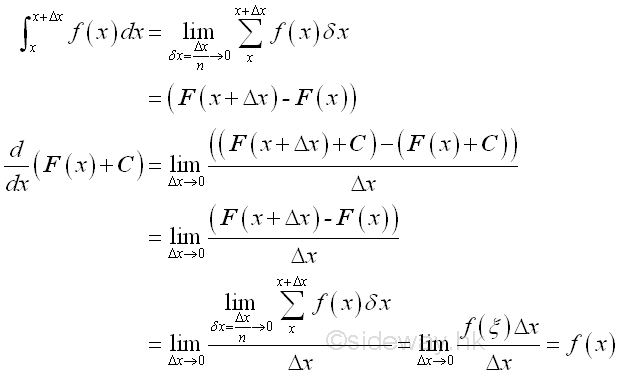
Imply 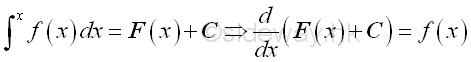
Therefore the indefinite integral is usually for the applications of determine the instantaneous effect of the function f(x) with respect to x at x. GraphicalGraphically, the definiation of integral for a non negative function is 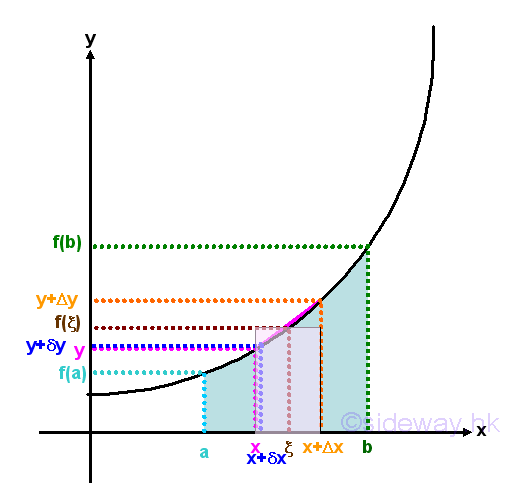
In deriving the integrals, the functions should be defined within the interval of interest and the integral is determined by the summation of infinitesimal elements of the product of the corresponding integrand and variable of integration Δx in which the infinitesimal elements of the actual integral of the function is approximated by making the length of interval Δx approaches zero or by making the number of subinterval Δx approaches infinity. Indefinite integral:For indefinite integral, the indefinite integral can also be determined by the summation of infinitesimal elements in the similar way. Since there always exists a point ξ equal to the mean value of the function between the interval x and Δx, the total area under the curve, Σ(f(x)Δx) can always be represented by the function f(ξ) between f(x) and f(x+Δx) times the interval Δx, i.e. f(ξ)Δx. When Δx approaching zero, function f(ξ) will also approaching function f(x) also. Imply the total area within the interval Δx is equal to f(x)Δx when Δx approaching zero. And using the concept of anti-differentiation, when taking the limit, the funcion f(x) is equal to the rate of change of the indefinite integral F(x) with respect to x. 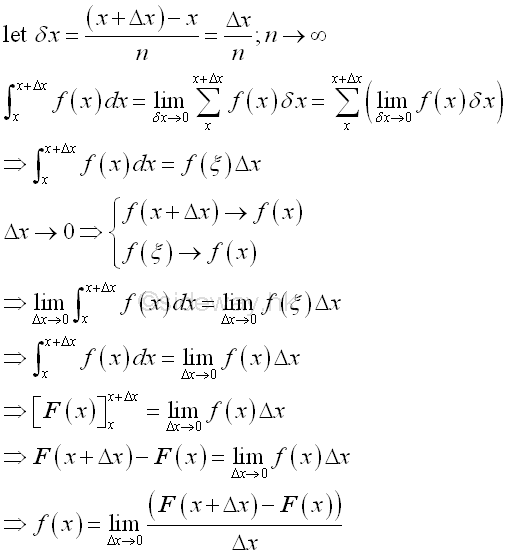
Since the integral with the same upper and lower limits is equal to zero, the constant of intergration is equal to -F(x). When Δx approaching zero, the indefinite integral at x+Δx approaches the indefinite integral at x. In other word, the indefinite integral is the instantaneous effect of f(x) at x. And for convenience, indefinite integral can be expressed as:: 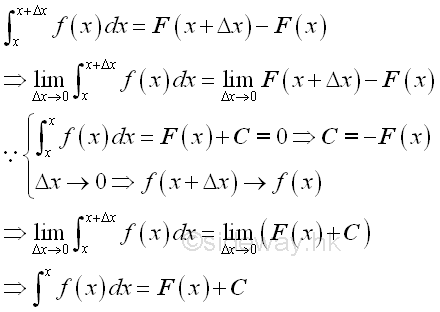
Therefore the integral of a function at x can be obtained by the anti-differentiation of the function plus a constant of integration.. Definite integral:Since the indefinite integral is the infinitesimal area element under the curve f(x) at x and the definite integral is equal to the total area under the curve f(x) between x=a and x=b, therefore the definite integreal can be obtained by adding up all the infinitesimal area elements between the interval. Imply the definite integrals can be computed in terms of the indefintie integrals. 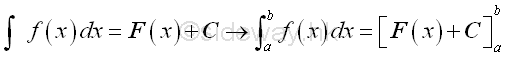
Definite integral is defined as the summation of infinitesimal function elements in the closed interval. Assuming the closed interval is divided into n subinterval, the value of an infinitesimal element can then be expressed as f(i)Δx or F(i) and the definite integral can also be obtained by the summation of all infinitesimal elements. The value of definite integral is therefore can be determined by applying the anti-differentiation concept. 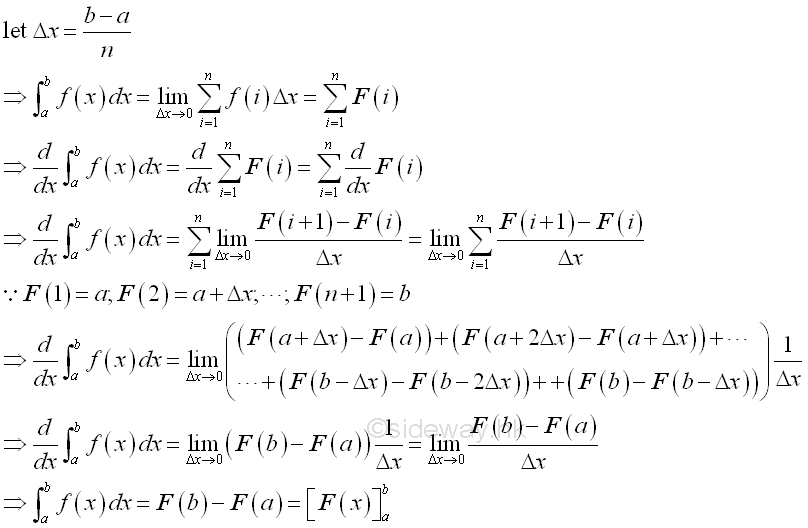
Through the anti-differentiation concept, the definite integral is determined by the summation of infinitesimal element. When the subinterval of the infinitesimal element is sufficiently small, the value of the function on the closed subinterval is bounded by the function on its lower and upper boundaries for all infinitesimal elements. And for any given epsilon greater than zero, a positive delta x can alway be found such that the difference of value of the function between the lower and upper boundaries is smaller than the epsilon for all infinitesimal elements. Since the infinitesimal element can be approximated as the differential change, the error of approximation is bounded 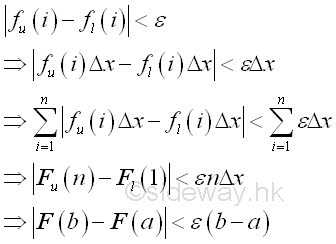
GeometricalThis is the mathematical description of integral in plane geometry. Geometrically, the infinitesimal element formed by the product of the corresponding integrand f(x) and variable of integration Δx is equal to a signed infinitesimal area of a rectangle, i.e.. positive above the x axis and negative below the x axis. An indefinite integral is therefore the infinitesimal area element of the function f(x) at x. And a definite integral is the net area bounded by the function f(x) between the closed interval [a,b]. As in plane geometry, an average value of the function f(x) can be determined by dividing the net bounded area over the length of closed interval [a,b]. When considering an infinitesimal area element with Δx approaching zero, the averge value of the function f(x) of the net area bounded by the function f(x) between the closed interval [x,Δx] is approximately equal to the function f(x). Since the net bounded area is equal to the difference between the two indefinite integrals of x and (x+Δx), function f(x) can be consided as the rate of change of the integral at x also. Or the indefinite integral is the anti-derivative of function f(x). PhysicalPhysically, when Δx approaching zero, the indefinite integral of function y with respect to x can be interpreted as the instantaneous effect of function y due to the change in infinitesimal dx at x. And the definite integral of function y with respect to x can be interpreted as the total effect of function y due to the change in infinitesimal dx between the interval [a,b]. In other words, this is the physical description of the integral. The plane geometry interpretation of integral can also be interpreted as the physical geometry in real life application by making use of the accumulative concept of infinitesimal area element. This is to interpret integration process as an accumulative value calculation process. In general, the integration process can be applied to any physical quantity which can be expressed in the form of value of accumulative concept. Similarly, the average value of physical quantity function over a closed interval can also be calculated by dividing the net value of bounded physical quantity over the length of closed interval [a,b] as in geometrical interpretion. The accumulative concept of a physical quantity is the summation of the value of infinitesimal physical quantity. Since the physical quantity of an infinitesimal element is the instantaneous effect of the physical quantity at x. And therefore when Δx approaching zero, the limit of the rate of change of two successive infinitesimal elements of the physical quantity is equal to the rate of the change of the physical quantity. In other words, the instantaneous effect is the anti-differentiation of the accumulative form of a physical quantity. ApproximationBesides when Δx approaching zero, the arc length of an infinitesimal element on the curve can also be approximated by the secant line using Pythagorean theorem as in differentiation. Therefore curve length can be determined by integration, if the curve can be expressed as pieces of accumulative arcs geometrically or the physical quantity can be expressed in the form of accumulative arcs physically. Geometrical InterpretationNet Bounded Area of a function:By definition, the definite integral obtained by the summation of infinitesimal elements between the interval [a,b]. An infinitesimal element is equal approximately to the signed area of the infinitesimal element when the number of element tends to infinity or Δx approaching zero. Therefore definite integral is equal to the total bounded area under the curve f(x) between x=a and x=b for a non negative function or equal to the net area function of the curve below and above the axis. 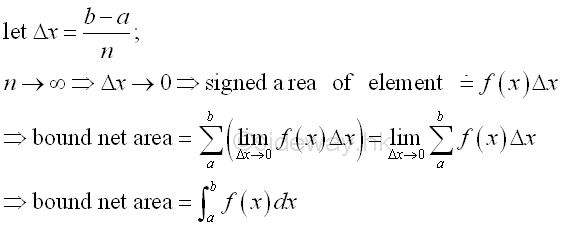
Average Value of function:Since the definite integral is obtained by taking the limit of the summation of all infinitesimal elements of f(x) between the interval [a,b], therefore for continuous function an average value of function f(x) can be obtained mathematically by dividing the definite integral over the length of its interval. 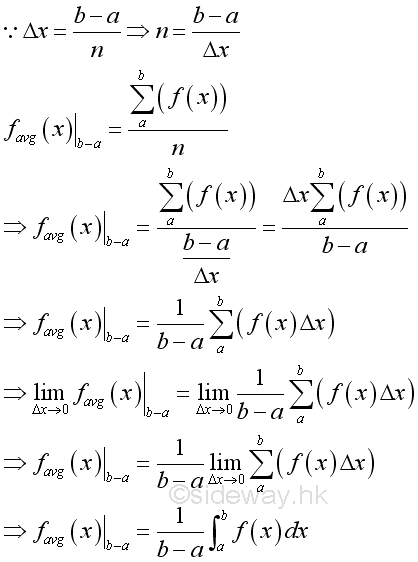
Anti-derivative of a function:The average value of function for an infinitesimal element can be defined in a similar way. Since definite integral is equal to the difference between the indefinite degral of the upper and lower limit, therefore the average value of a function can also be expressed as the average rate of change of the indefinite integral at x. By taking the limit of the function, the average value of the function is equal to the intantaneous value of the function as Δx approaching zero. In other words, the indefinite integral is the anti-derivative of a function. 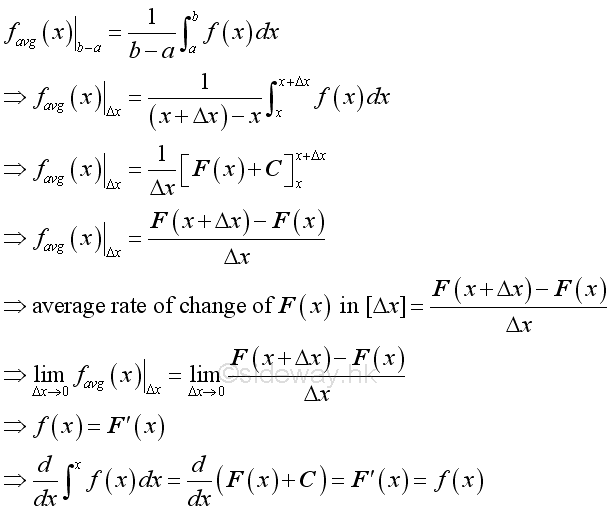
Physical InterpretationIntegration as Summation of Accumulative Physical Quantity:The geometrical interpretations of integrals provide the basic concepts for all real life applications by applying the concept of accumulative physical quantity. Physically, integral can be interpreted as the effect or result of the accumulative mathematical model of a real life application due to the variable of integration obtained by the method of integration. The key step of the applyication of integration in real life application is the convertion of the mathematical model of a real life application in the form accumulative physical quantity. For example, the area of a right angle triangle is equal to half of the height times the base. When using integration, the hypotenuse of the right angle triangle can be formulated as a function of the base of the triangle, x, so that the accumulative physical quantity of the triangle can be expressed as f(x)Δx. The accumulative physical quantity is an infinitesimal rectangular area element of the triangle with f(x) as the length and Δx as the width. By taking the limit, the summation of infinitesimal rectangular area elements of a right angle triangle can be expressed as an integral over the interval of the base of the triangle. And the determination of the area of a right angle triangle is equal to the calculation of area under a curve as in geometrical interpretation, Imply 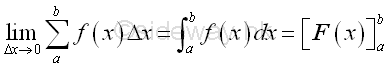
Integration can be applied to any physical quantity which can be converted into accumulative format in a similar way. And definite integral can be used to determine the total physical quantity over a closed interval. The function F(x) is therefore the total effect or result of the accumulative element function f(x) with respect to x within the closed interval. In the determination of the right angle triangle area case, the infinitesimal accumulative element is defined as the result of the integrand f(x) equal to the height with respect to x due to the differential change Δx and the result of the infinitesimal accumulative element is equal to the infinitesimal area element. 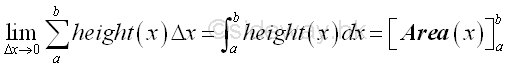
Similarly, if the accumulative element function f(x) is defined as the cross-section area of a right angled triangular prism, i.e heigh x length, then the result of the infinitesimal accumulative element due to the differential change Δx is equal to the infinitesimal volume element of a right angled triangular prism . 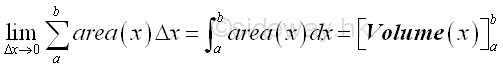
This is the way to express a physical quantity in an accumulative form using a differential change along the dimension of interest. Average value of Accumulative Physical Quantity function:Definite integral is defined the summation of infinitesimal accumulative element over a closed interval. Since the infinitesimal accumulative element is the differential element along the interval of interest, the definite integral is equal to the summation of the accumulative element function f(x) over the closed interval. When taking the limit, the average value of the accumulative element function f(x) can be obtained by dividing the accumulated physical quantity by the length of the closed interval. 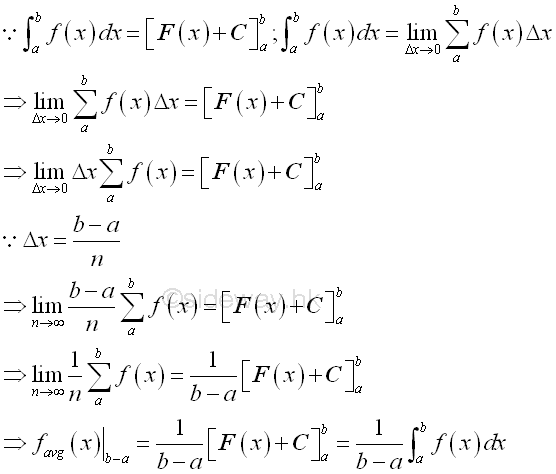
As in the definite integral of the area of a right angle triange, the accumulative element function f(x) is the height of the hypotenuse along the interval of interest. For subinterval with equal length, the definite integral is equal the summaton of all accumulative element functions over the closed interval times the differential subinterval. When the numerber of subinterval tends to infinity, the definite intergral is equal to the total accumulative element function f(x) with respect to x over the closed interval. And therefore the average of the accumulative element function f(x) can be obtainted by dividing the definite integral by the length of the closed interval. 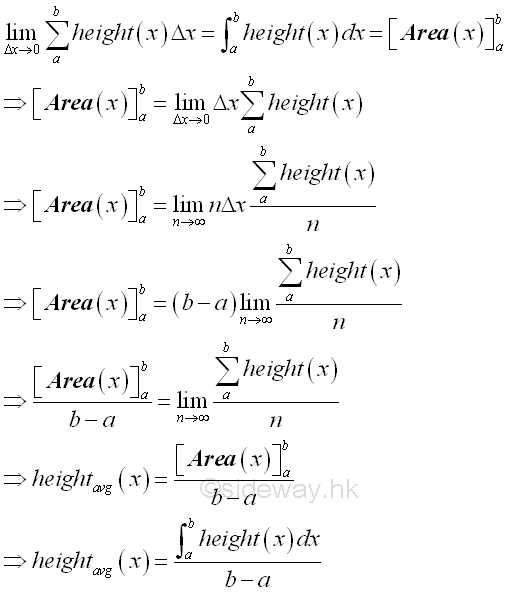
Anti-derivative of an Accumulative Physical Quantity function:Sometimes the concern for deal with physical quantity is the intantaneous rate of change. The definite integral of the subinterval can be determined as usual. In other words, the difference between the two indefinite integrals is equal to the accumulative element function f(x) times the differential change Δx. When the differential change Δx approaching zero, the equality becomes the instantaneous quantity at x. Therefore the instantaneous accumulative element function f(x) at x can be expressed as the rate of change of the net effect or result of accumulative element function f(x). Since the net effect or result of accumulative element function f(x) over the closed interval Δx is equal to the differential change of the indefinite integral F(x) at x, the accumulative element function f(x) can be expressed as the derivative of the indefinite integral F(x) at x. 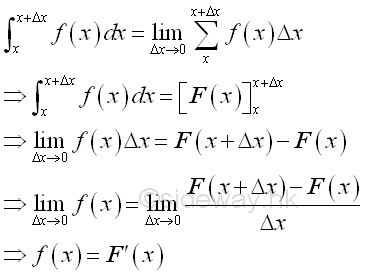
For example, considering the accumulative element function f(x) of the right angled triangular prism example is defined as the volume flow rate with respect to x, the integral becomes the total intantaneous volume of the flow at x. In other word the rate of change of the total intantaneous volume of the flow at x is equal to the volume flow rate with respect to x. 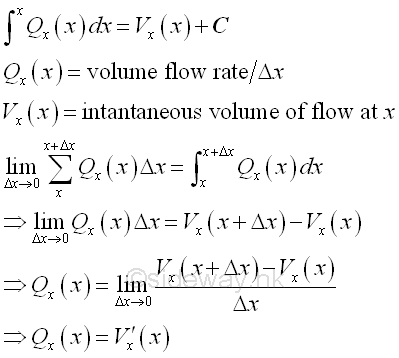
ApproximationGeometrical Length of a functionFor a continuous function, the length of a function is equal to the curve length s of the curve of a function. Therefore the length of a function can be determined by the summation of the curve length Δs of an infinitesimal subinterval Δx by dividing the curve into n equal subintervals over the closed interval [a,b]. 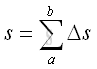
When Δs approaching zero, the length of a function can be determined by intergration. 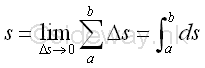
As the curvature approximation in the application of differentiation, the arc length of an infinitesimal curve element can be approximated by the secant line joining the boundary points of the infinitesimal curve element when Δx approaching zero. Using the Pythagorean theorem. Imply
By substitution, the length of the function over the closed interval [a,b] is:
Approximation of Accumulative Physical Quantity:When the accumulative physical quantity is expressed in terms of the curve length of a function, the physical quantity can be determined by integration through the approximation of curve length by secant line. For example, the length s of the hypotenuse of a right angle triangle can be determined by integration through the application of Pythagorean theorem. Imply
Similarly, if the accumulative element function f(x) is defined as the circular cross-section of the lateral surface area of a right circular cone, i.e 2πy, then the result of the infinitesimal accumulative element due to the differential change Δs is equal to the infinitesimal surface area element of a right circular cone.
Therefore, the lateral surface area S of a right circular cone.
|
Sideway BICK Blog 15/11 |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||