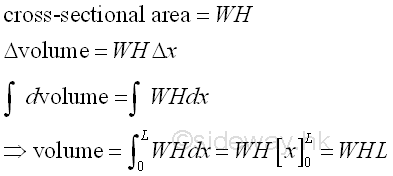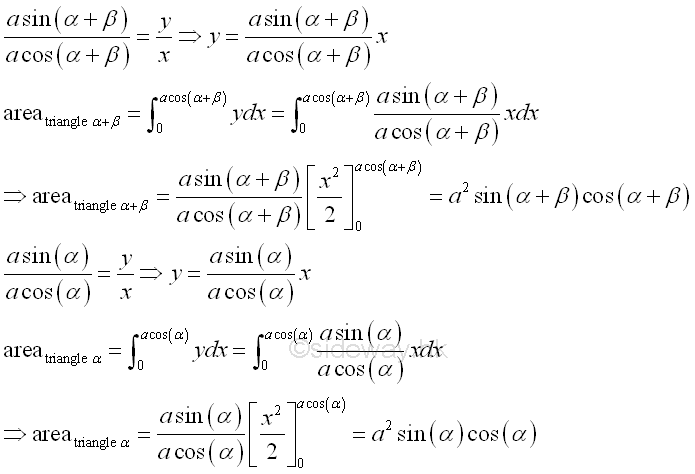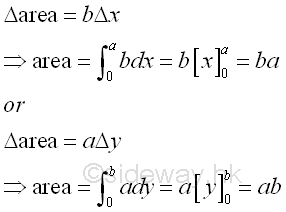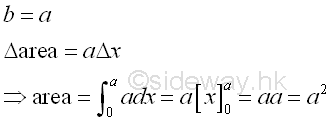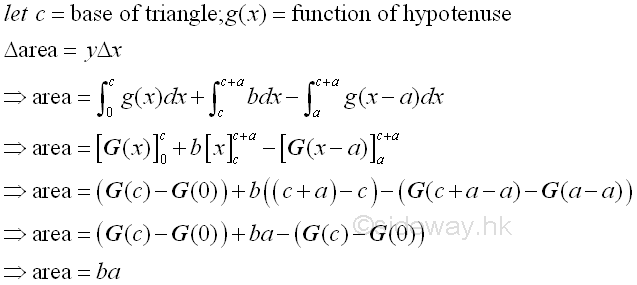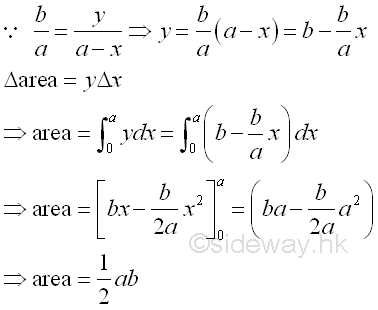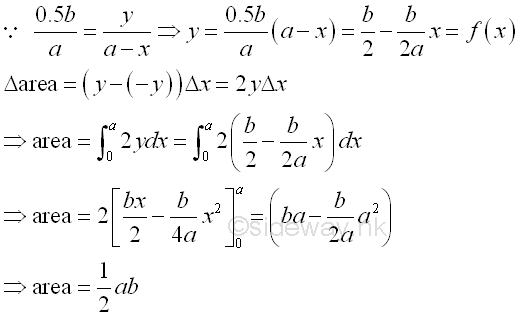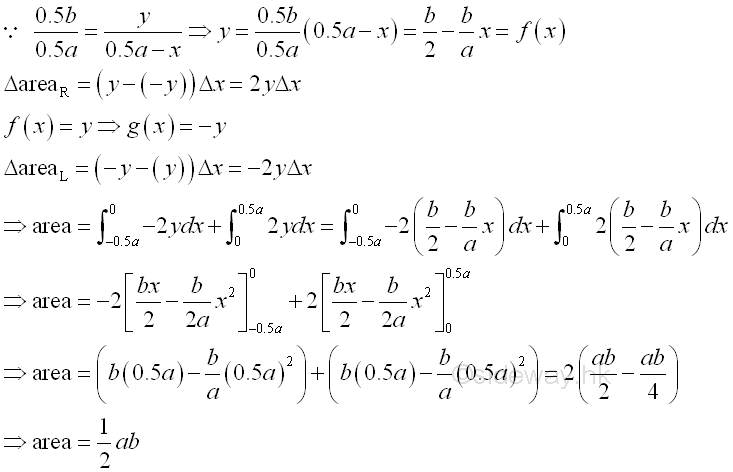Sideway
BICK BLOG from Sideway
Sideway
BICK BLOG from Sideway
|
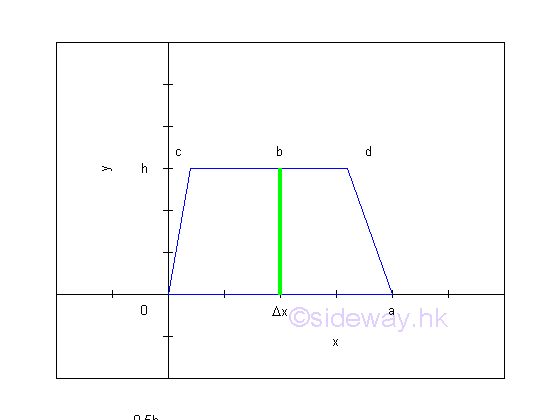
Link:http://output.to/sideway/default.asp?qno=111100015 Volume of Common Solids Summation of Accumulative Physical QuantityVolumes of common solid can be determined by integration when the volume of a solid is expressed as an infinitesimal volume element that can be summed by the application of integration. 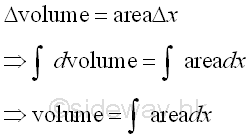
The infinitesimal volume element can be formed by the extrusion of a filled profile or the revolution of a profile. Volumes of Common Solids
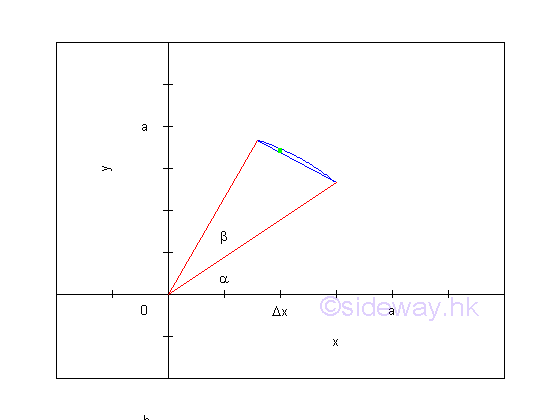
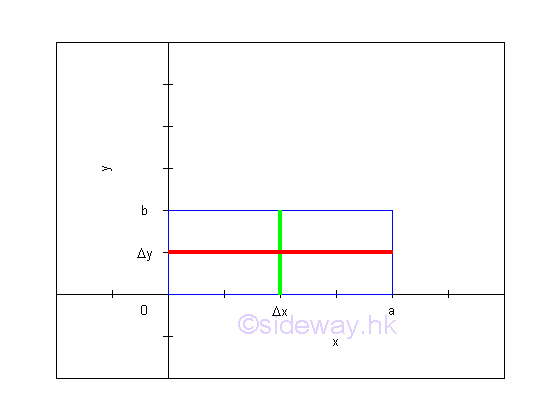
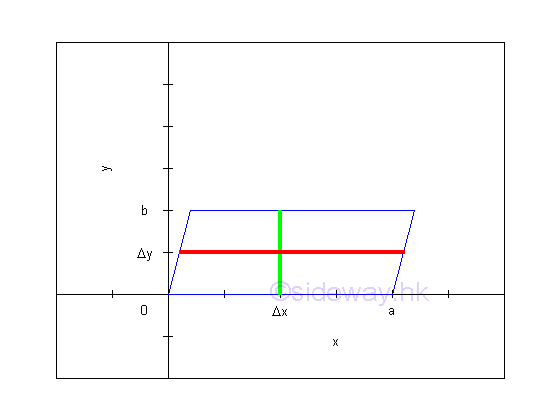
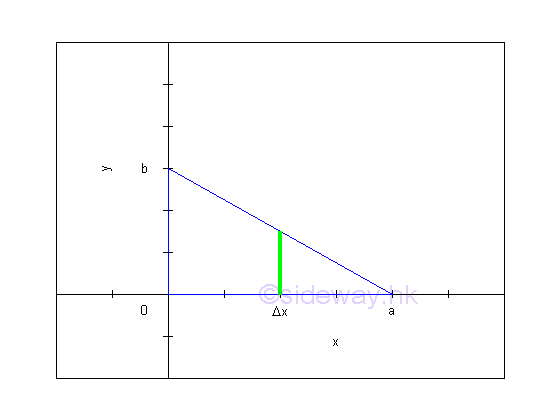
Link:http://output.to/sideway/default.asp?qno=111100013 Area of Plane Shapes Summation of Accumulative Physical QuantityAreas of plane shapes can be determined by integration when the area of a plane shape is expressed as an infinitesimal area element that can be summed by the application of integration. 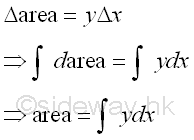
Areas of plane shapes
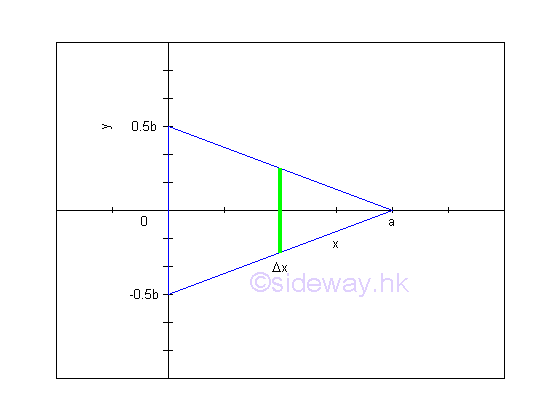
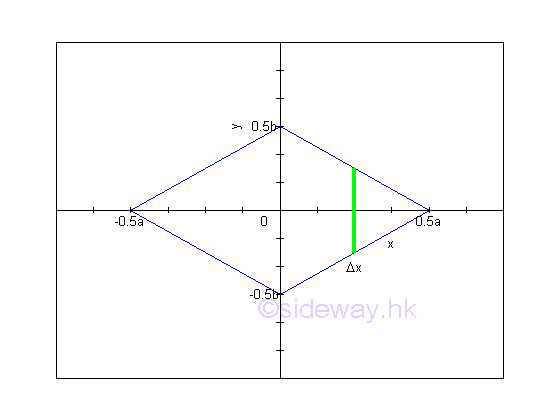
Link:http://output.to/sideway/default.asp?qno=111100012 Area of Plane Shapes Summation of Accumulative Physical QuantityAreas of plane shapes can be determined by integration when the area of a plane shape is expressed as an infinitesimal area element that can be summed by the application of integration. 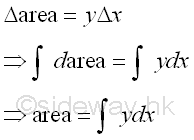
Areas of plane shapes
|
Sideway BICK Blog 27/11 |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||