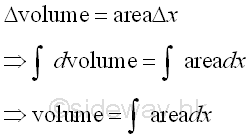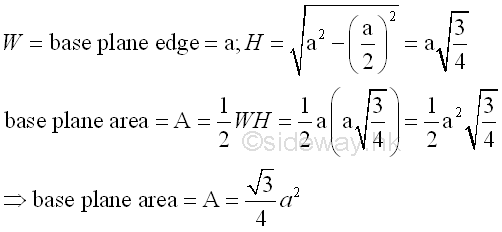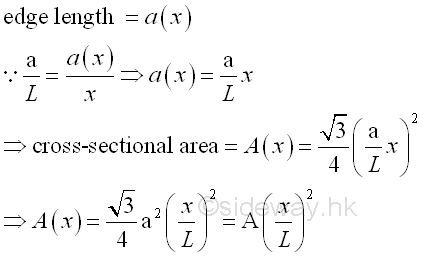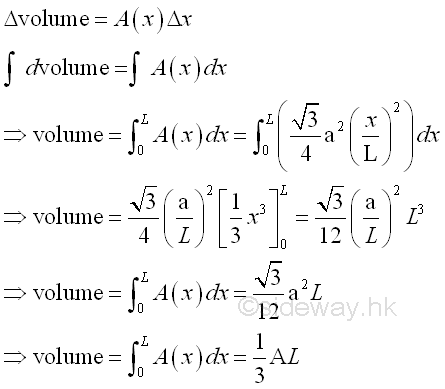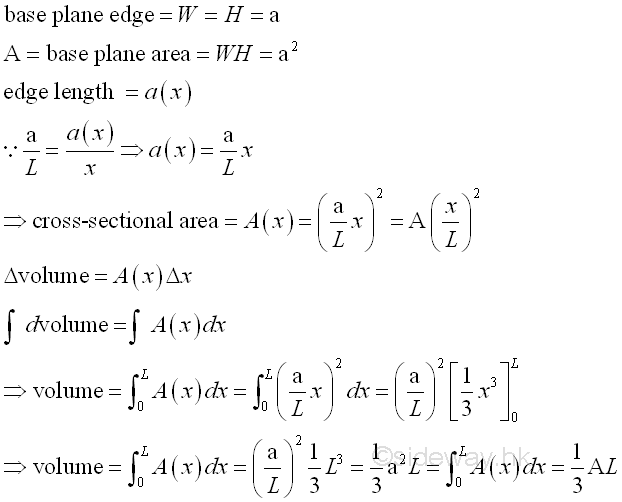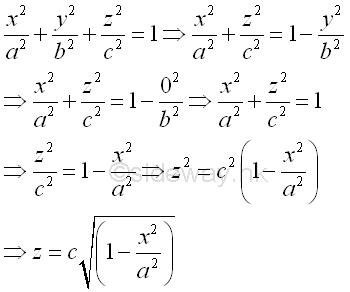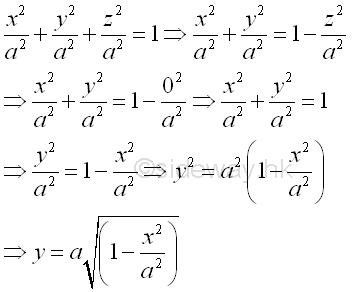-
Volume of Tetrahedron or Triangular Pyramid
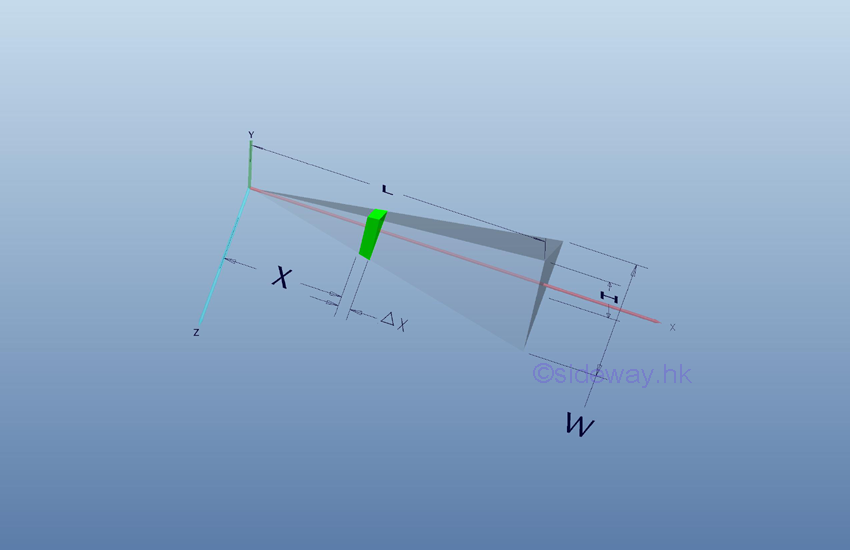
The base area of the tetrahedron in terms of base plane edge
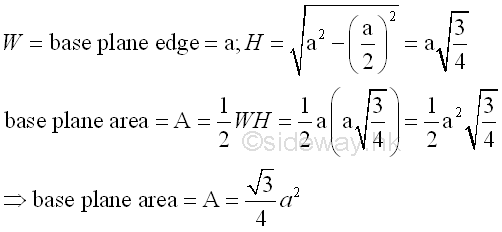
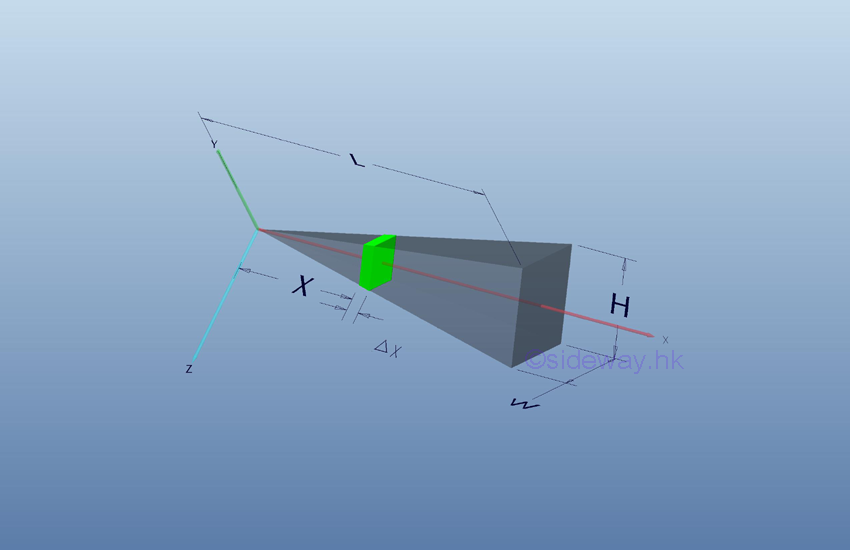
The cross-sectional area of a tetrahedron varies with x, imply
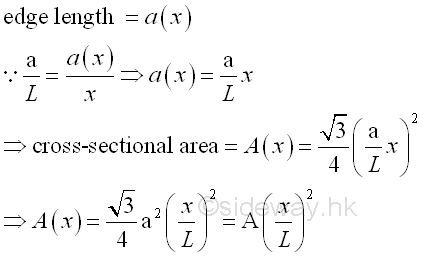
Volume
of tetrahedron by horizontal summation approach.
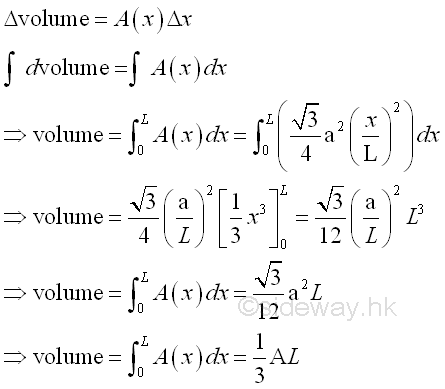
-
Volume of
Regular Tetrahedron
Volume of regular tetrahedron is a
special case of tetrahedron. The volume of regular tetrahedron can be obtained
by letting all edges of the tetrahedron are the same, e.g a.

-
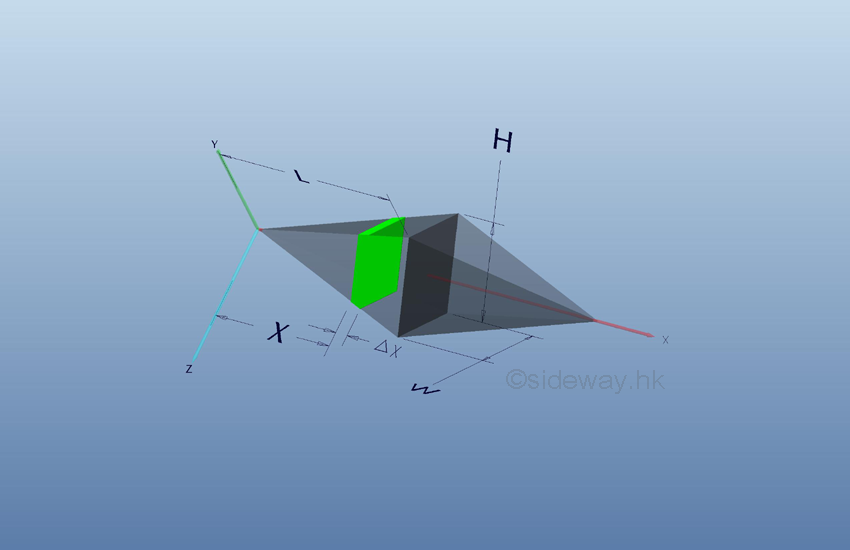
Volume of
Retangular Pyramid
Volume
of rectangular pyramid by horizontal summation approach.

-
Volume of
Square Pyramid
Volume of square pyramid is a
special case of retangular pyramid. The volume of square pyramid can be obtained
by letting W=H
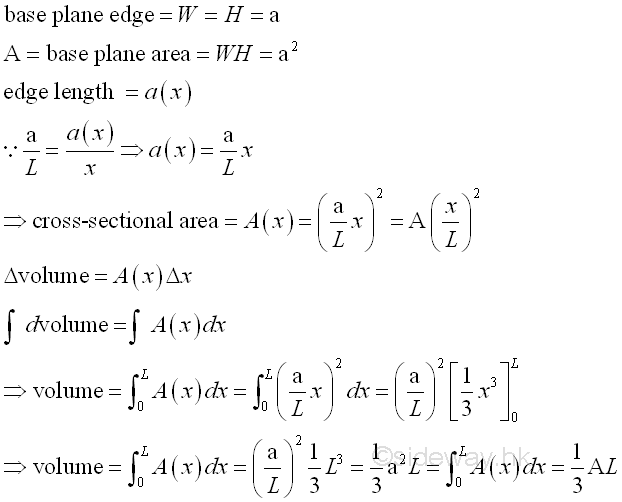
-
Volume of
Pyramid
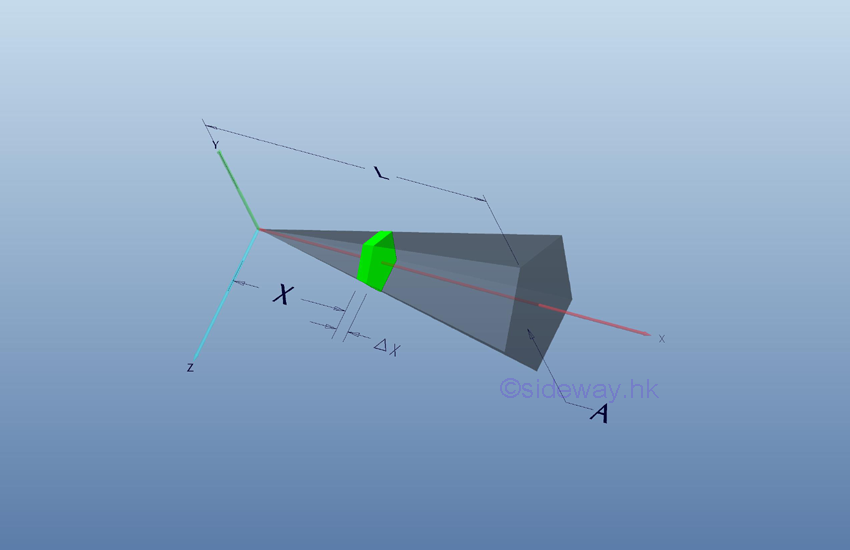
Volume of pyramid is a
general polyhedron of pyramid with a polygonal base. The volume of a pyramid can
be obtained by the base plane area of the polygonal base and the height of the
polyhedron.

-
Volume of Cone
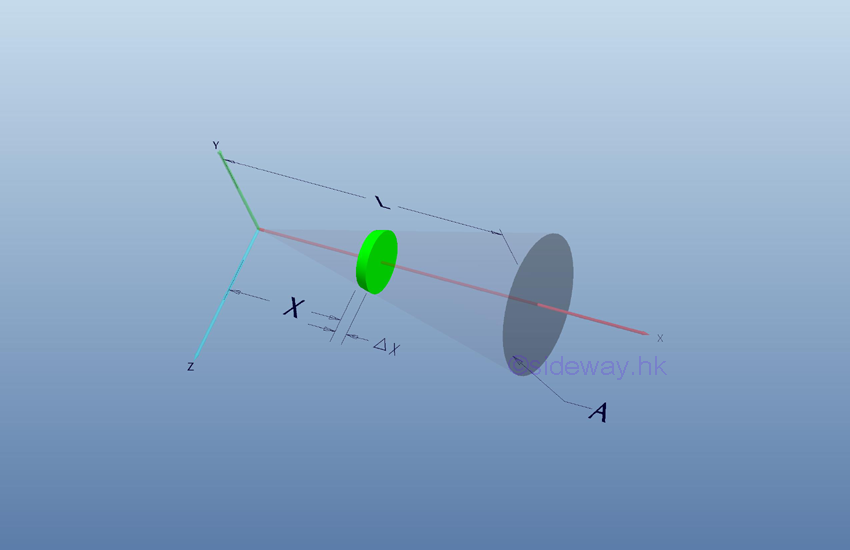
Volume
of cone can be obtained by the base plane area of the cone base and the height of
the cone as in pyramid.
Volume
of cone by horizontal summation approach.

-
Volume of
Octahedron
Volume of octahedron or square bipyramid can be formed from two
square pyramids by joining its mirror image about the base of the square
pyramid. Therefore the volume of a square bipyramid is equal to the total volume
of two square pyramid. In general, a n-gonal bipyramid is a polyhedron
formed by two
general polyhedron of pyramid with a polygonal base and the two pyramids are
arranged by base to base. Therefore the volume of a bipyramid is equal to the
total volume of two pyramids.

-
Volume of Ellipsoid
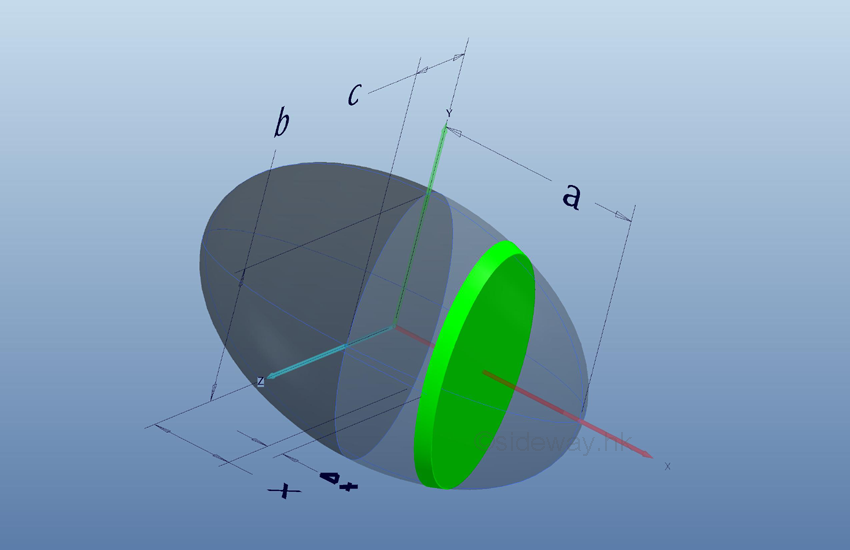
Volume
of ellipsoid can be obtained by the summation of cross-sectional area of the
ellipsoid along cross-sectional profile.
The base plane area normal to x axis is,

The cross-sectional profile at y=0,
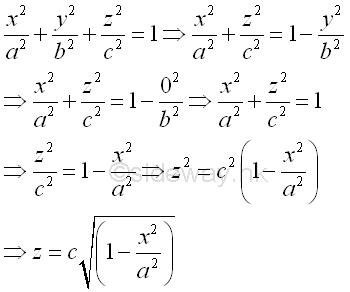
The cross-sectional profile at z=0,
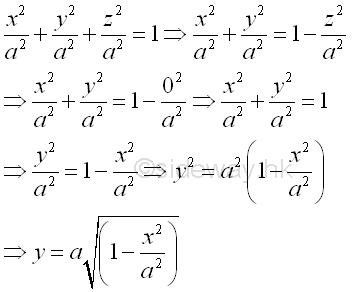
Volume of ellipsoid by horizontal summation approach.

 Sideway
BICK BLOG from Sideway
Sideway
BICK BLOG from Sideway