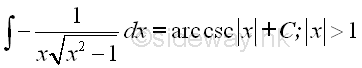Sideway
BICK BLOG from Sideway
Sideway
BICK BLOG from Sideway
|
Link:http://output.to/sideway/default.asp?qno=111100008 Anti-derivative of a Function Anti-Derivative of a FunctionWhen considering the average value of a function on a small closed interval Δx, there also exist a mean function value f(ξ) lying on the curve of the function f(x). When the length of subintervals approaching zero, the mean function value of a function on the closed interval Δx will be approaching to f(x) also. Therefore the mean function value of the definite integral of a function f(x) on an infinitesimal interval, Δx is equal to the value of function f(x). By expanding the definite integral of the function f(x) on an infinitesimal interval, Δx, the mean function value f(ξ) is then equal to the change of the integral with respect to x. When taking the limit as Δx tends to zero, function f(x) can therefore be interpreted as the differentiation of the indefinite integral. Imply 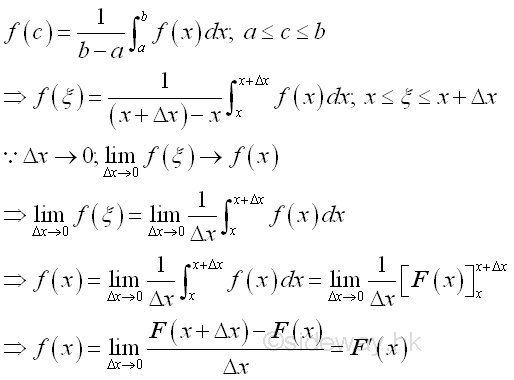
Anti-Derivative of simple functionIndefinite integrals of Derivatives of Polynomials
Indefinite integrals of Derivatives of Trigonometric Functions
Indefinite integrals of Derivatives of Exponential and Logarithmic Functions
Indefinite integrals of Derivatives of Inverse Trigonometric Functions
|
Sideway BICK Blog 25/11 |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
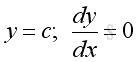 imply
imply
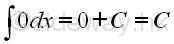
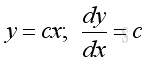 imply
imply
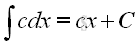
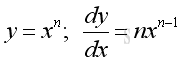 imply
imply
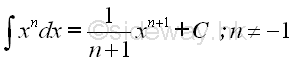
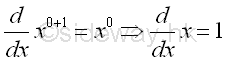 imply
imply
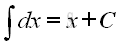
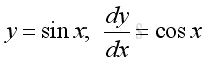 imply
imply
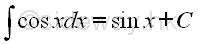
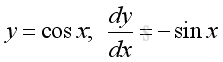 imply
imply
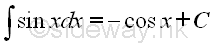
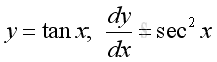 imply
imply
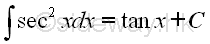
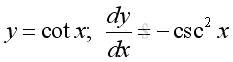 imply
imply
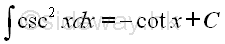
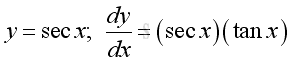 imply
imply
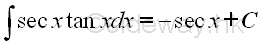
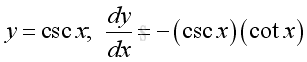 imply
imply
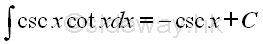
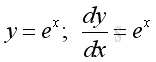 imply
imply
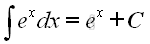
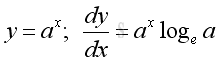 imply
imply
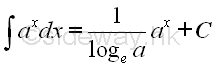
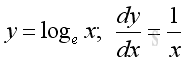 imply
imply
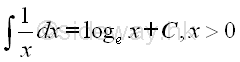
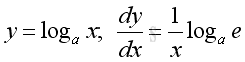 imply
imply
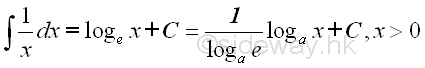
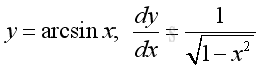 imply
imply
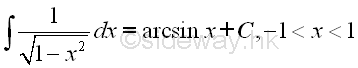
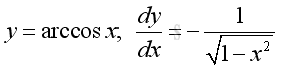 imply
imply
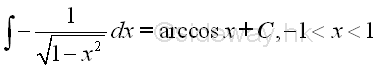
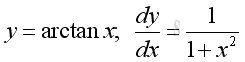 imply
imply
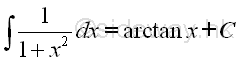
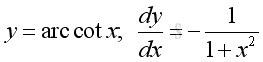 imply
imply
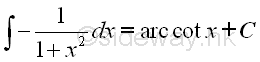
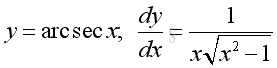 imply
imply
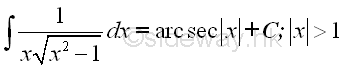
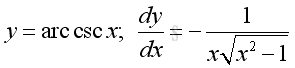 imply
imply