 Sideway
BICK BLOG from Sideway
Sideway
BICK BLOG from Sideway
|
Link:http://output.to/sideway/default.asp?qno=111100007 Average Value of a Function Average Value of a FunctionAverage value of a function on the interval can be approximated by the summation of the value of a function of all subintervals over the number of subintervals. Since definite integration can be considered as the summation of infinitesimal elements on a closed interval. When the number of subintervals approaching infinity, the average value of a function can be determined by the definite integration of the function over its length of integration. Imply 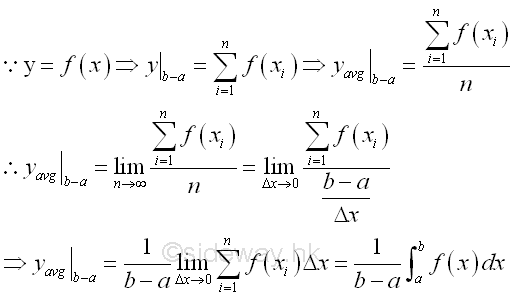
Average Function ValueFor example: function f(x)=(50x)1/3-1 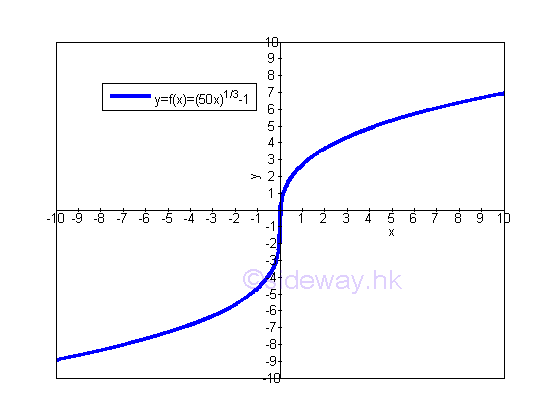
An approximation of function f(x)=(50x)1/3-1 on the interval [-8,6] by dividing the interval into 14 subintervals. The average value of the function f(x) on the interval [-8,6] can be obtained by taking the average of these 14 values. 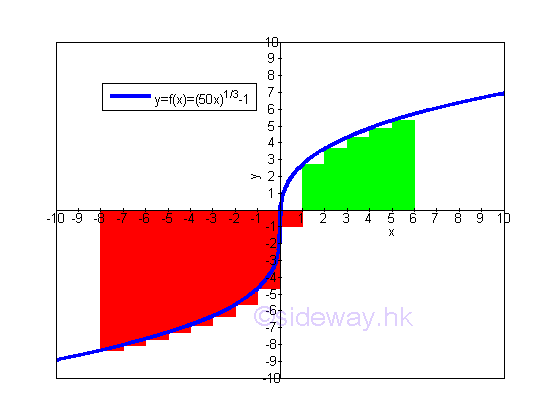
More accurate average function value can be obtained by increasing the number of subintervals. When the number of subintervals approaching infinity or the length of interval approaching zero, imply 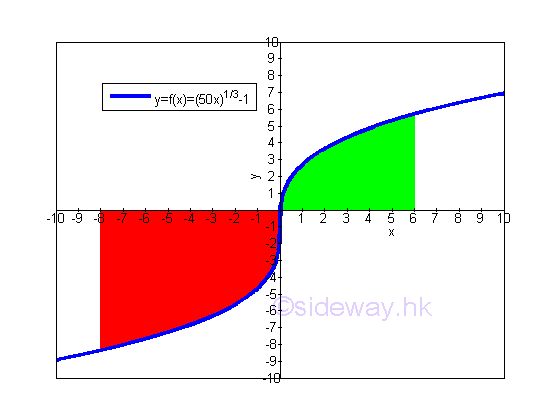
Therefore, the average function value of function f(x)=(50x)1/3-1 on the closed interval [-8,6] is 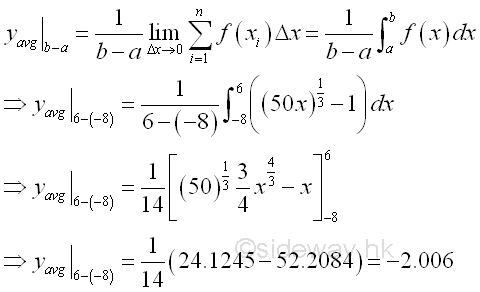
Since definite integral is the net value of the sum of infinisimal elements. the average function value is the signed value of the function on the closed interval. Graphically, 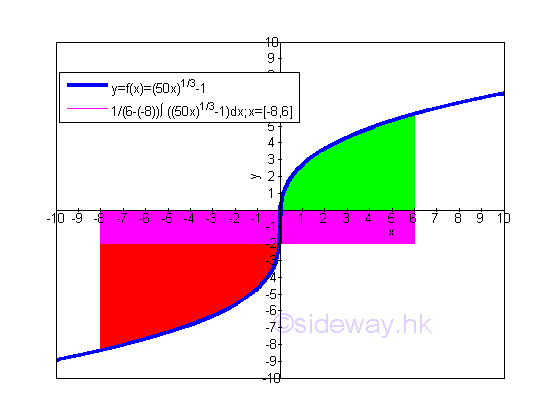
Mean Function ValueSince the function f(x) is continuous on closed interval [a,b], the average funcion value should always lie on the curve of the function, therefore there is alway a number c on the closed interval [a,b] such that mean function value f(c) is equal to the average function value. 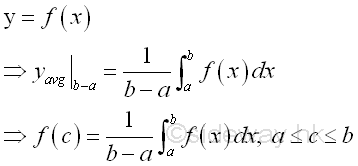
The number c can be obtained by equating the average function value and the mean value function. imply 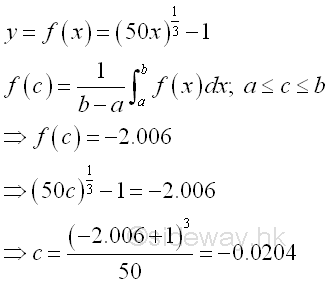
Graphically, the intersection of function in an enlarged view is 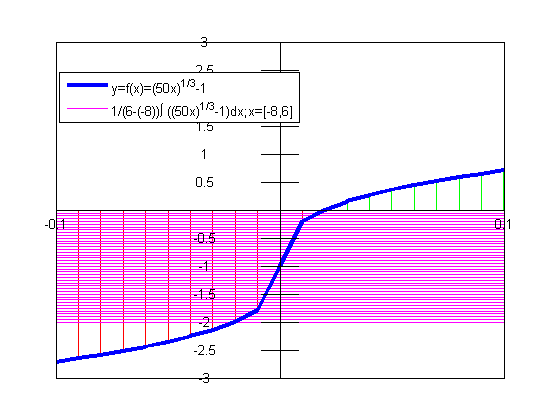
|
Sideway BICK Blog 24/11 |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||

