 Sideway
BICK BLOG from Sideway
Sideway
BICK BLOG from Sideway
|
Link:http://output.to/sideway/default.asp?qno=140200019 Calculus of Vector Function Kinematics: Calculus with Vector Functions for MotionMotion in two or three dimension can be described by vector functions of a single variable which can have the common form, r(t)=<f((t),g(t)> for 2D, rr(t)=<f((t),g(t),h(t)> for 3D where f((t),g(t) and h(t) are the componet functions of the vector function. In order to make the vector function make continuous and defined, all component functions should be continuous and defifned within the domain set of variable t of the vector function. Limits of Vector Function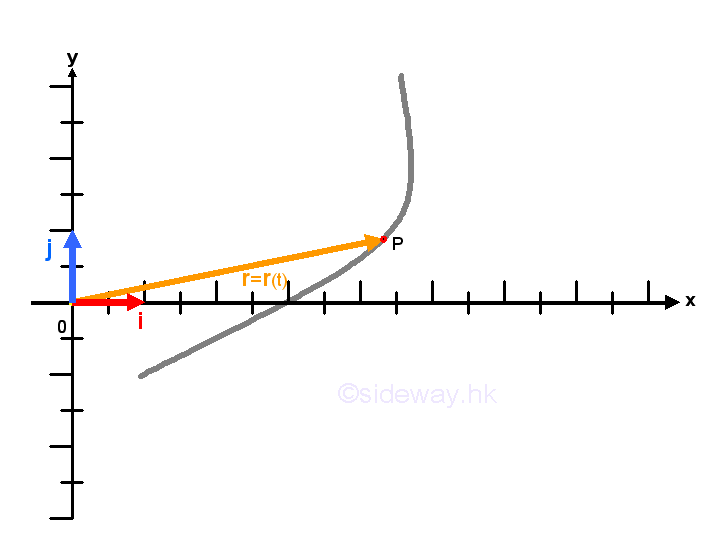
In a general sense, the limit of a vector function is equivalent to the limit of the function of a vector or equal to the limit of all component functions of the vector function. In kinematic 2D or 3D motion, the vector function usually depends on a single real number parameter time, t, that is r(t). And standard unit vectors, i, j, and k, of Cartesian or rectangular three dimensional space with coordinate x,y, and z can also be used to express the vector function as a specific type of vector-valused function such that the vector function can be represented by an algebraic vector expression. Imply 
Derivative for Vector Function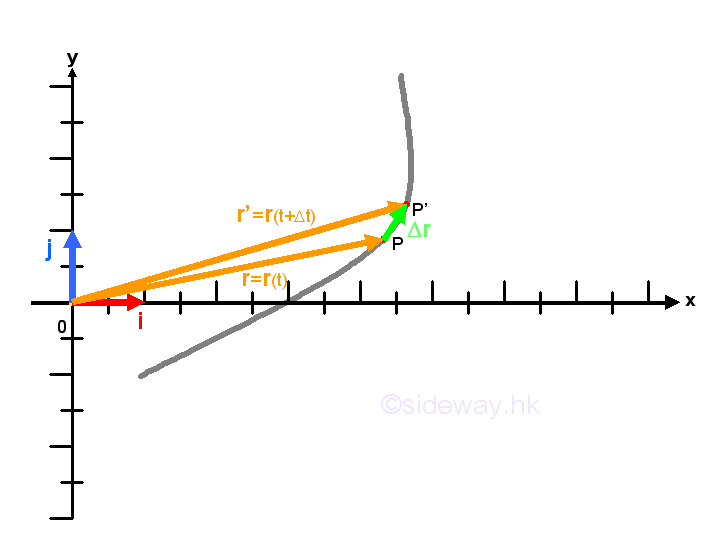
The derivative for vector functions can be derived from the definition of derivative, that is the rate of change of the vector function with respect to independent variable during a infinitely small interval of the independent variable. The change, Δr, of the vector function is equal to the final vector r(t+Δt) minus the initial vector r(t) and is same as the vector joining vector r(t) to vector r(t+Δt) during interval Δt. Geometrically, the change of the vector function due to the small interval can also applied to the component function as in finding limit also. Imply 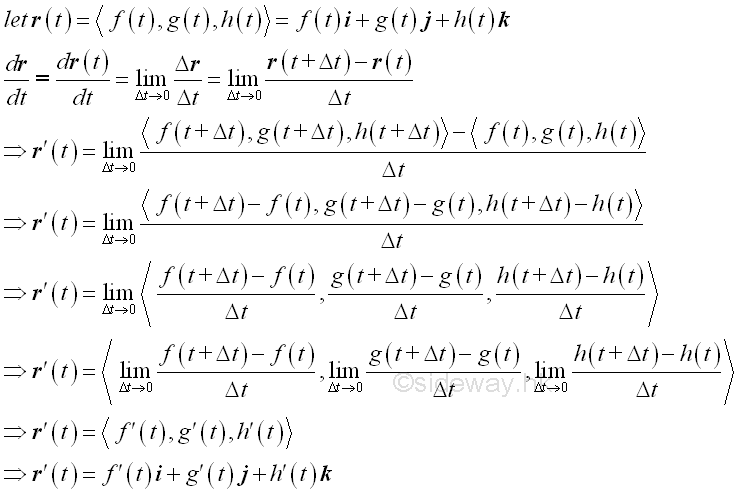
For the expression of a vector-valued function, the form of the derivation of a vector-valued function remains unchange because the functional expression of a unit vector only have a magnitude of a one unit constant along the direction of the coordinate axis and is independent of the independent varible, the derivatives of a unit vector is always equal zero and therefore the derivative of a product of functions remains only the unit vector parts and the derivatives of the unit vector parts are always equal to zero. Imply 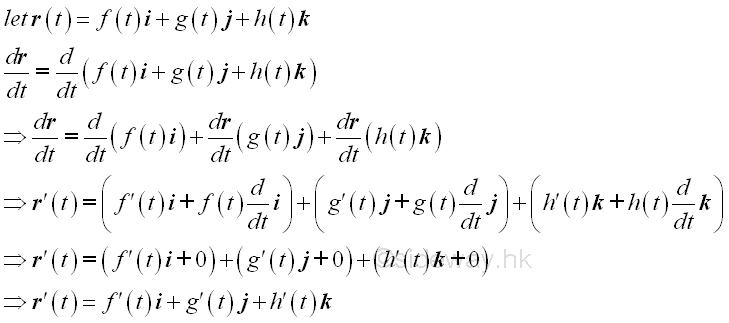
According to the vector-valued function, the change Δr in a vector function can be considered as a fixed ratio of the changes of component functions in term of the indepentent variable t. When the change Δr in a vector function is equal to zero, all changes of component function become zero also. However, when the change Δt of the indepentent variable approaches zero and is sufficiently small, the changes Δr in vector function during the interval Δt can be approximated by a linear function with respect to the independent variable t. In other words, the limiting vector r'(t) or <f'(t),g'(t),h'(t)> is a non-zero vector tangent to the curve with respect to t. Unlike, the curve representing a function with respect to a independent variable at which the derivative of the function equals to zero which indicates that the function has a horizontal tangent line, the path representing a vector function with respect to a independent variable at which the derivative of the vector function equals to zero means that the changes is equal to zero at a point or direction of change abruptly. Rules of Differentiation for Vector FunctionIn general, most standard rules of differentiation can also be extended to vector function. Constant Multiple of Vector Function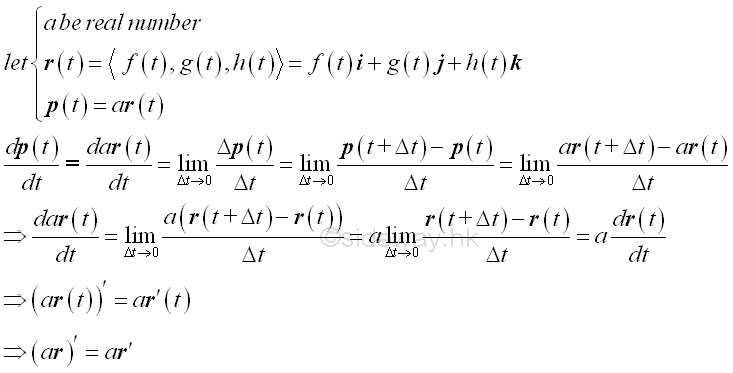
Sum of Vector Functions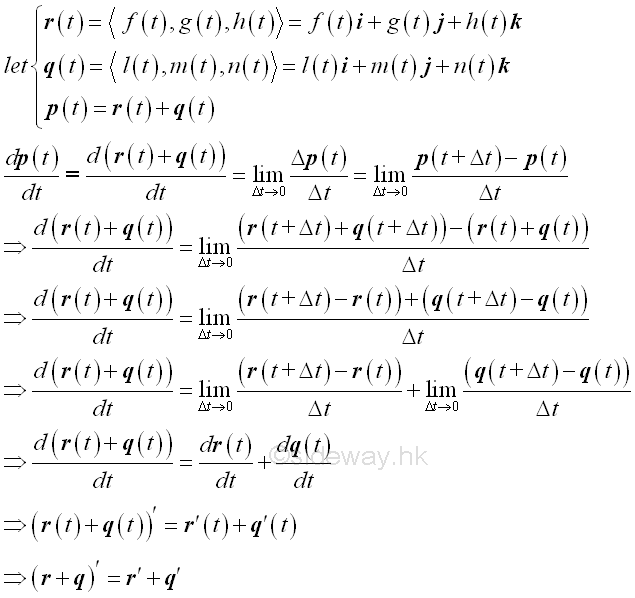
Product of Scalar Function and Vector Function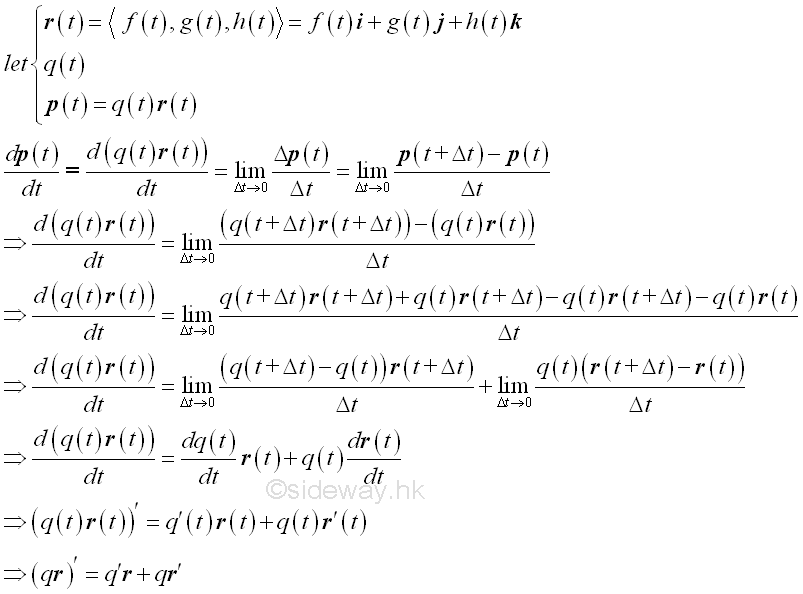
Scalar Product of Vector Functions
Vector Product of Vector Functions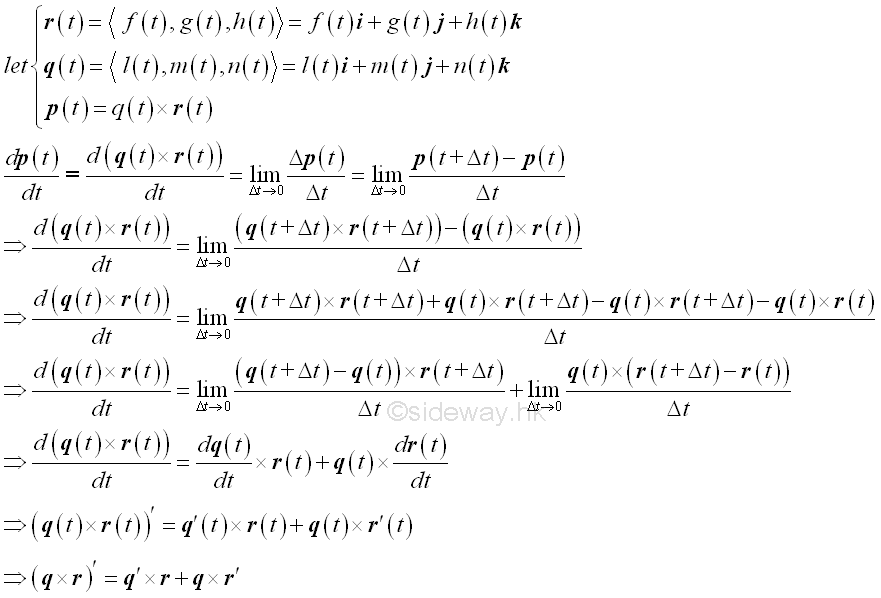
Composite Vector Functions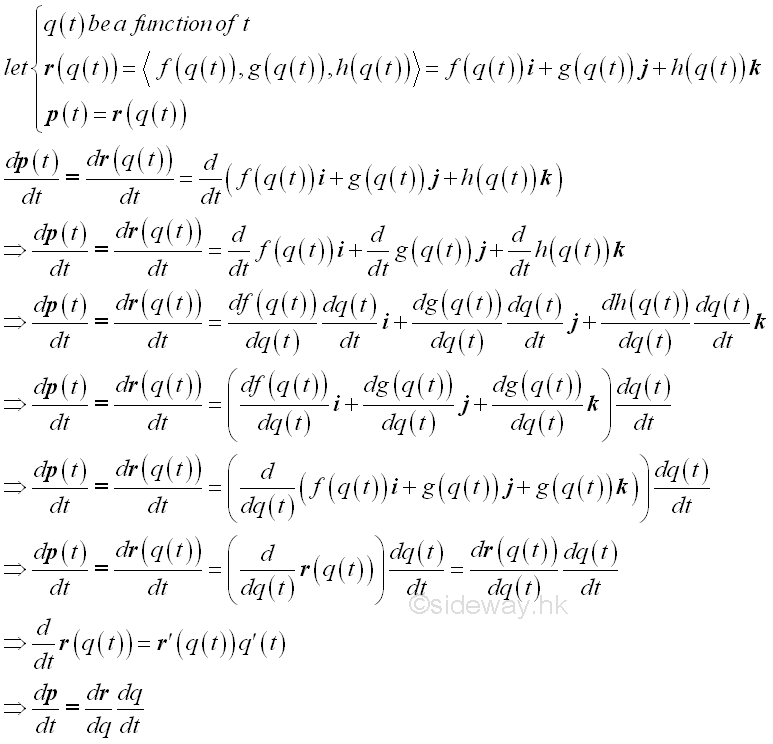
Integral for Vector FunctionSince the integral of a function can be considered as the antiderivative of the function, the integral for vector function can be derived similarly. 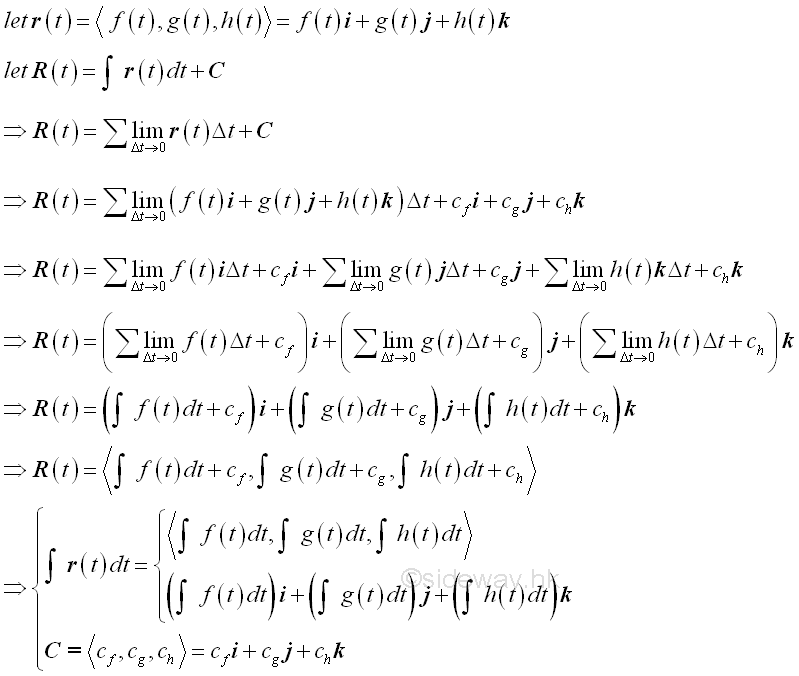
Similarly, the definite integrals are defined as following. 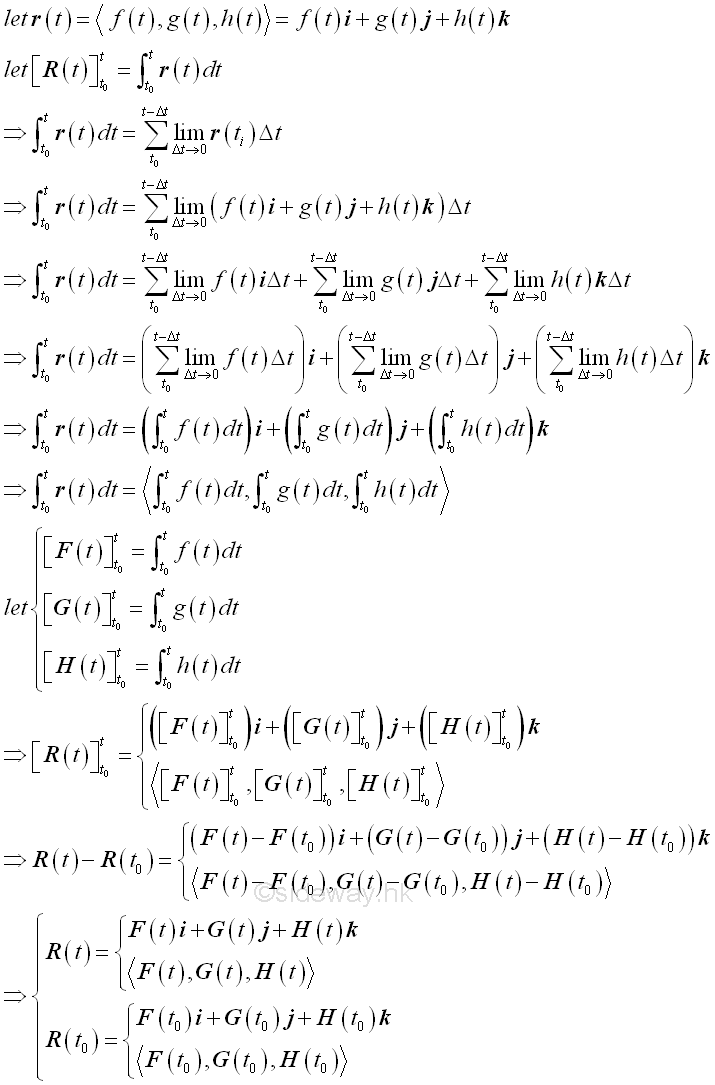
|
Sideway BICK Blog 19/02 |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||

