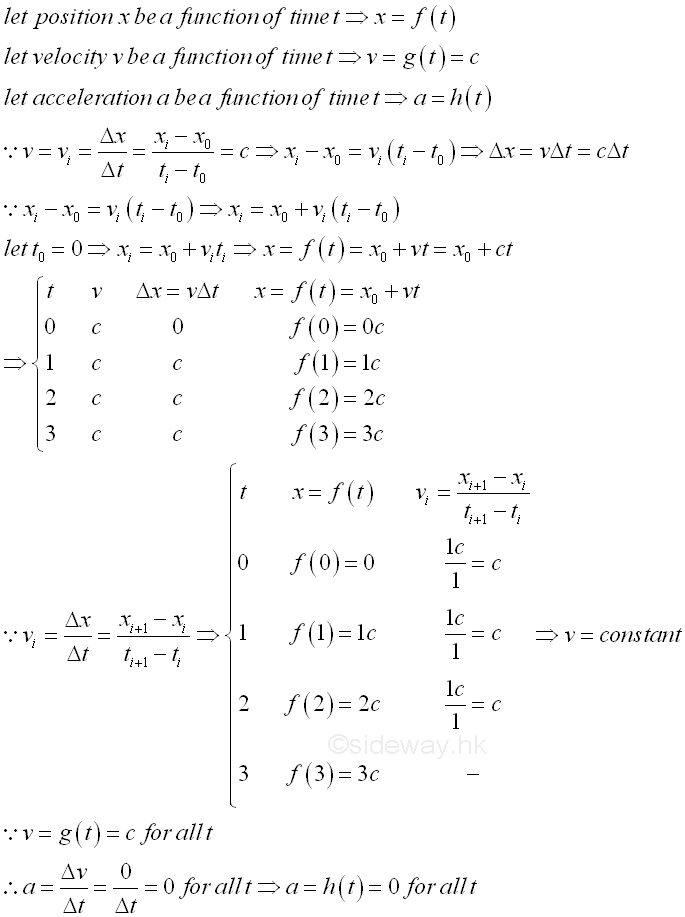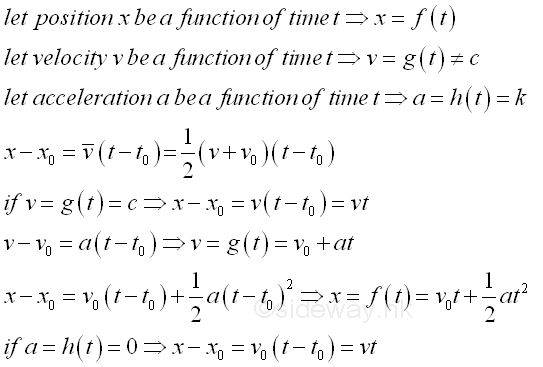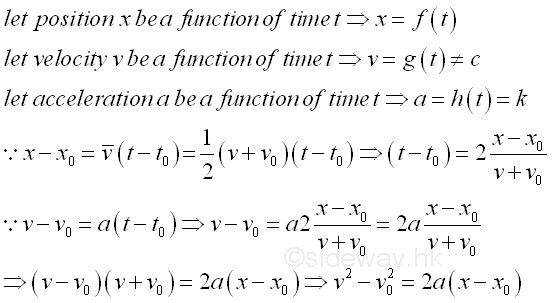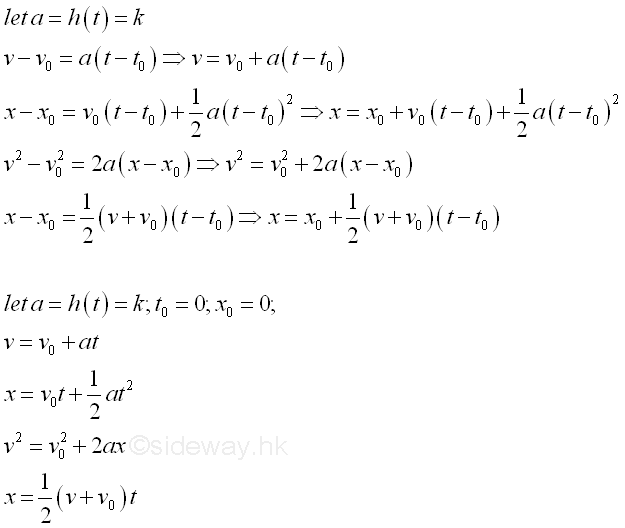Equations of Kinematics

From the definitions of position, displacement, velocity, and acceleration, there exists a set of relationships between these quantitise. For simple regular motions, there are some basic equations of kinematics to calculate the unknown quantity from the known quantity.

Constant Situations

Simple motions with constant situations can be used to derive basic equations of 1D kinematics.

Constant Position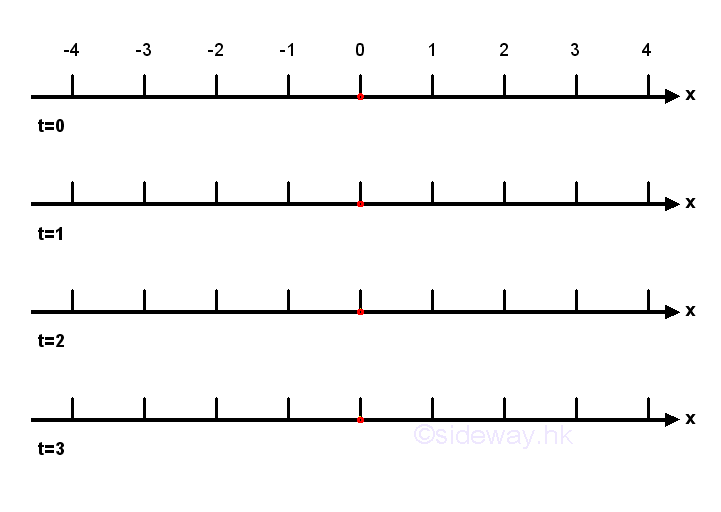

An object does not have any motion when the object is maintained in constant position. Since the object does not move, the velocity of the object must be equal to zero. And since the velocity does not change, the acceleration must be equal to zero also. 

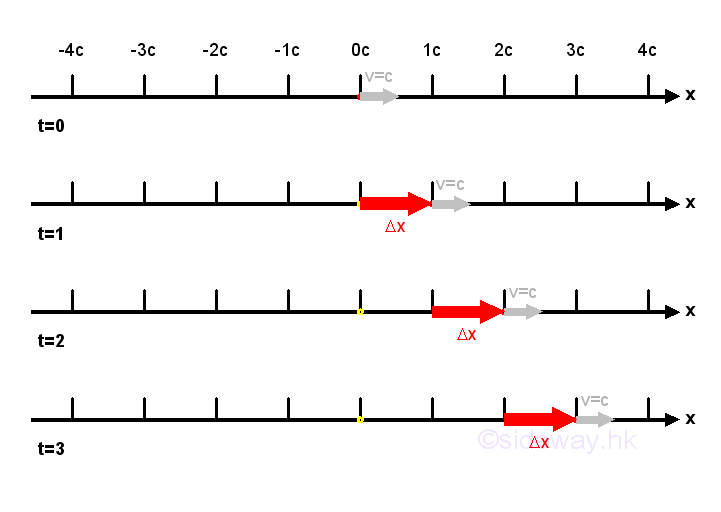
Constant Velocity

 

When an object is maintained in constant velocity, the object moves by the same distance in same direction during each equal time interval. As the object moving in constant velocity, the displacement between each interval is equal to a constant, the position of the object is changed in a regular manner and can be determined by the definition of velocity accordingly. Since the object moves constantly, the motion is called uniform motion and the acceleration is equal to zero.

 

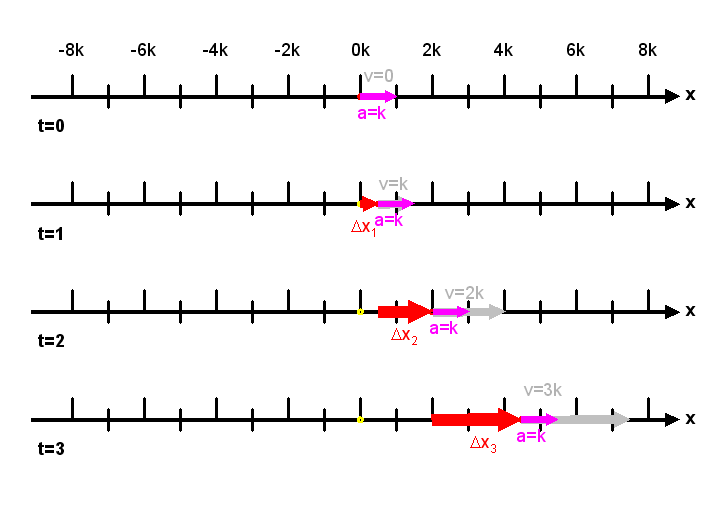
Constant Acceleration

 

When an object is maintained in constant acceleration, the object changes the same amount of velocity in same direction during moving in each equal time interval. As the object moving in constant acceleration, the changes in velocity  between each interval is equal to a constant, the velocity of the object is changed in a regular manner and can be determined by the definition of acceleration accordingly. Since the object accelerates constantly, the motion is called uniform acceleration motion and the acceleration is equal to a constant.

 

Under constant acceleration, the velocity of an object changes linearly with time. Since the velocity of the object varies with time, the object does not move the same distance during each equal time interval. Instead, the position of the object changes more rapidly as a function of time. Since the velocity of an object changes linearly with time, both the final velocity of the object in each time interval can be determined if the initial velocity of the object is known and the average velocity of an object in each time interval can then be obtained from the average of initial and final velocity also. And the displacement for each time interval can also be determined by the definition of average velocity accordingly.

 

If initial velocity of an object is equal to zero, then the displacement of the object is proportional to the sqaure of the time interval and is equal to at2/2.

Equations of Kinematics

From the constant situations, equations of kinematics are derived to calculate unkown quantity for the motion of an object with constant acceleration as following.

 

From the first two equations of kinematics, there is a common term (t-t0) that can be eliminated. Therefore another equation of kinematics can be derived.

 

For the case of constant acceleration, the four equations of kinematics are.

 

Examples

Example 1

A car travels from position A to position B with a speed of v1m/s and then returns from position B to position A with a speed of v2m/s. The average speed for the whole journey is

 

Example 2