 Sideway
BICK BLOG from Sideway
Sideway
BICK BLOG from Sideway
|
Link:http://output.to/sideway/default.asp?qno=140200017 Graphical Method of 1D Motion Graphical Method of 1D MotionFrom the fundamental kinematic equations, the motion of an object is described with respect to time. These functions can therefore be represented by plotting ordered pairs in the Cartesian plane graphically. Geometrical Representation of 1D MotionThrough the graphical method, the geometrical meaning of 1D motion can be visualized. Derivative of a FunctionMotion as the derivative of a function. That is 
A position function x is a funtcion time t. For example, x=t+t2+t3 and the slope at t, dx/dt is equal to the velocity v at t 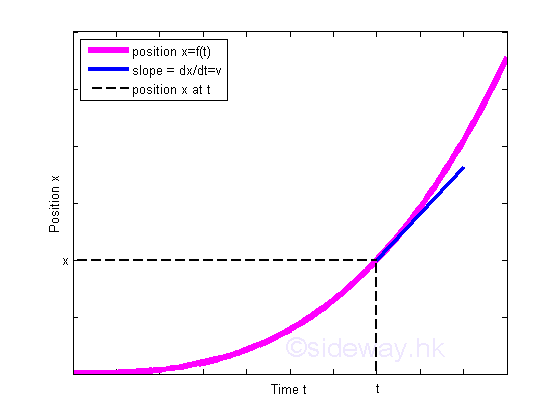
By definition, a velocity function v is the derivative of the position function with respect time t. Imply v=dx/dt=1+2t+3t2 and the slope at t, dv/dt is equal to the acceleration a at t. 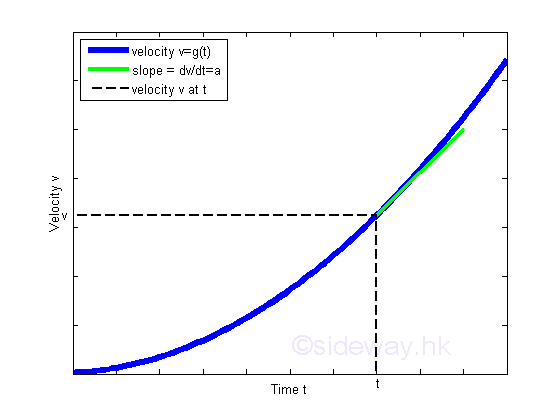
By definition, an acceleration function a is the derivative of the velocity function with respect time t. Imply a=dv/dt=2+6t . 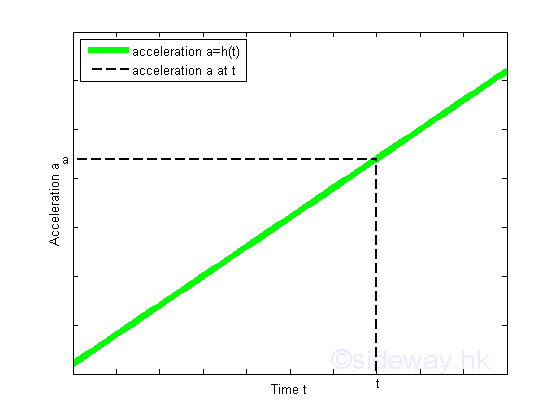
When motion functions can be expressed in term of position x, an acceleration function a is the product of the velocity function and the derivative of the velocity function with respect position x. 
For example, v=1+2x+3x2/40. Imply a=vdv/dx=(1+2x+3x2)(2+6x)/1600. Using the same scale of magnitude, the acceration a at x can be directly obtained by constructing the normal to the tangent line at x and the accelertation at x is then equal to the x-intercept or the subnormal accordingly. 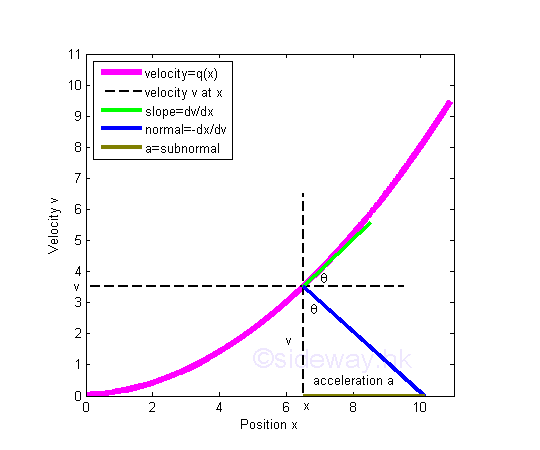
Integral of a FunctionMotion as the integral of a function. That is 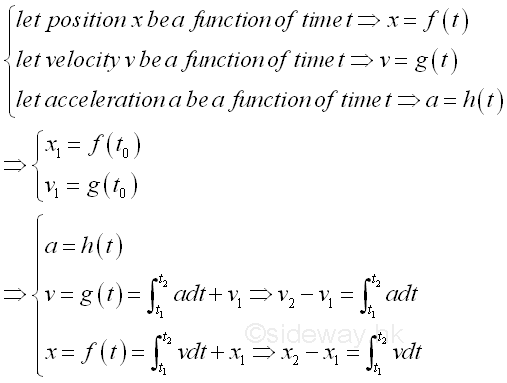
By definition, a velocity function v is the integral of the acceleration function with respect time t. Imply v2-v1=∫t2 t1 adt. 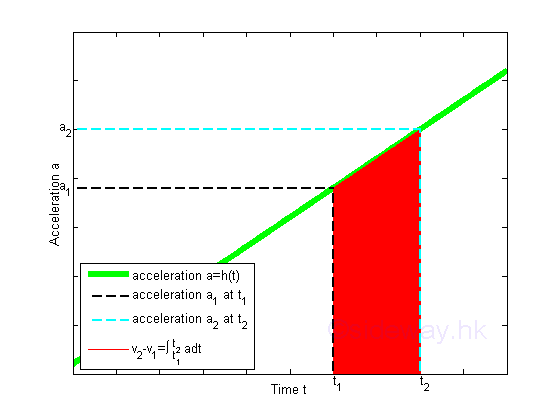
By definition, a position function x is the integral of the velocity function with respect time t where v2-v1=∫t2 t1 adt. Imply x2-x1=∫t2 t1 vdt. 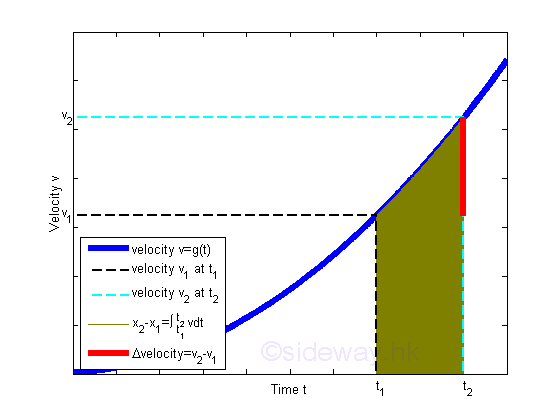
A position function x is a function of time t where x2-x1=∫t2 t1 vdt. 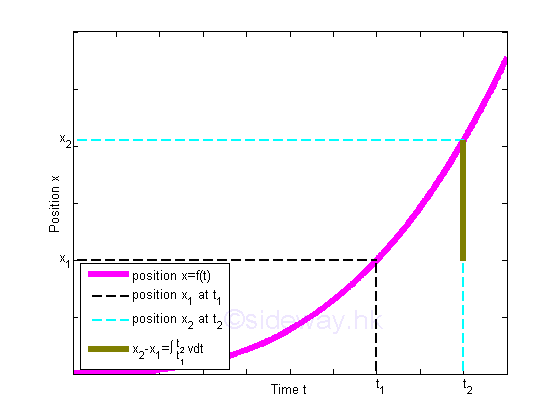
When motion functions can be expressed in term of velocity v, through transformation of areas, the difference between two positions can be expressed in another form. 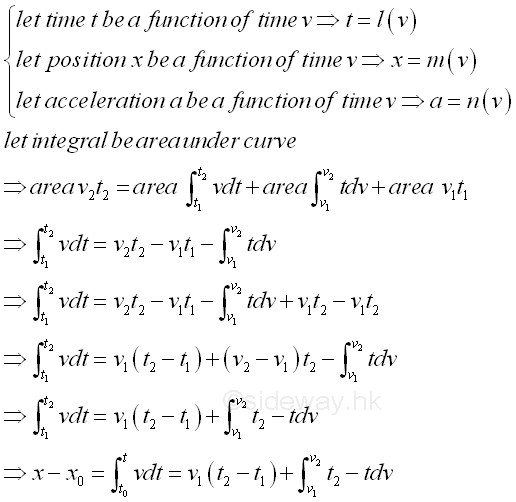
Imply. 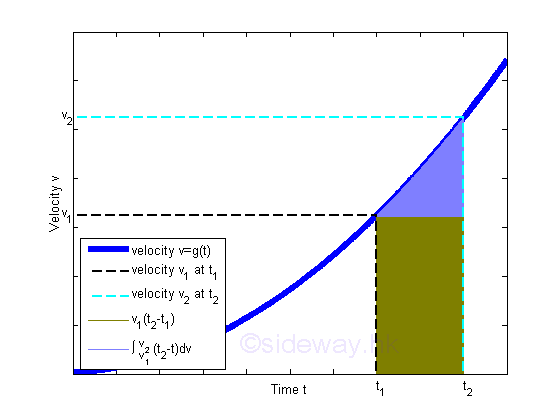
Through subsitution, the difference between two positions can also be expressed in another form associated with the acceleration function. By making use of the concept of moment-area method, the difference between two positions cab be easily obtained from acceleration with simple bounded areas. 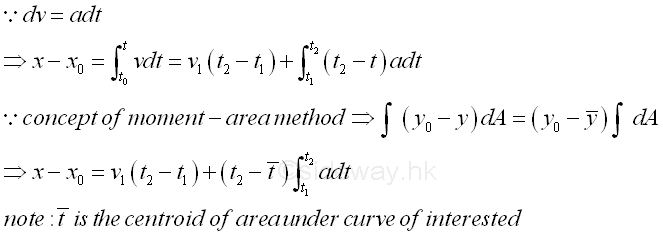
Imply 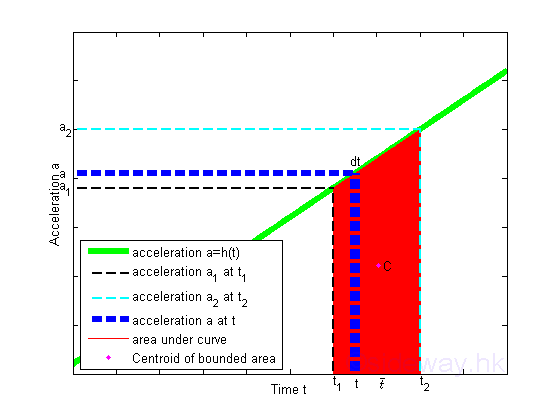
|
Sideway BICK Blog 17/02 |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||

