Equations of Kinematics

From the definitions of position, displacement, velocity, and acceleration, there exists a set of relationships between these quantitise. Basic equations of kinematics can be used to calculate the unknown quantity from the known quantities for simple uniform acceleration motion. But in most cases, the acceleration is not constant, that is the motion changes with time.

Instantaneous Situations

Simple motions expressed in terms of a function of time can be used to tackle general 1D kinematics problems at which the instantaneous motion of an object is being studied. And uniform acceleration motion is a special case of 1D kinematics problems only.

Position as a function of time

If the position of an object can be expressed in term of a function of time, f(t), the position of the object can be determined by time t. For example x=f(t)=-8+t+t2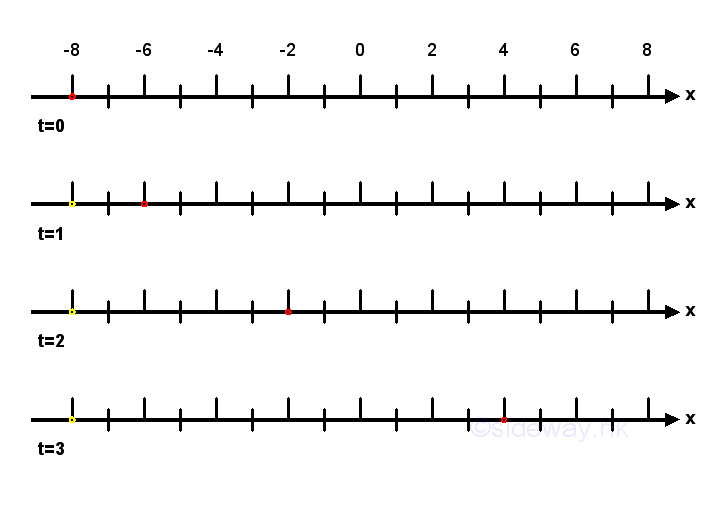

Since the object moves continuously, the displacement Δx in a time interval Δt can be expressed in term of a function of time t and Δt also, that is Δx=f(t+Δt)-f(t). By definition, velocity of an object is equal to the rate of displacement or change of position x in a time interval. From calculus, by the definition of derivative, the rate of change of position x with respect to time t when taking limit as Δt approaching 0 is equal to the derivative of the positon function f(t) with respect to time t. In other words, velocity is equal to the derivative of the position function, that is v=dx/dt=1+2t. Imply

The velocity of the object is therefore can be obtained from the position function f(t) and be expressed as a function of time, that is v=g(t)=1+2t. Imply velocity can be determined by the velocity function g(t) directly.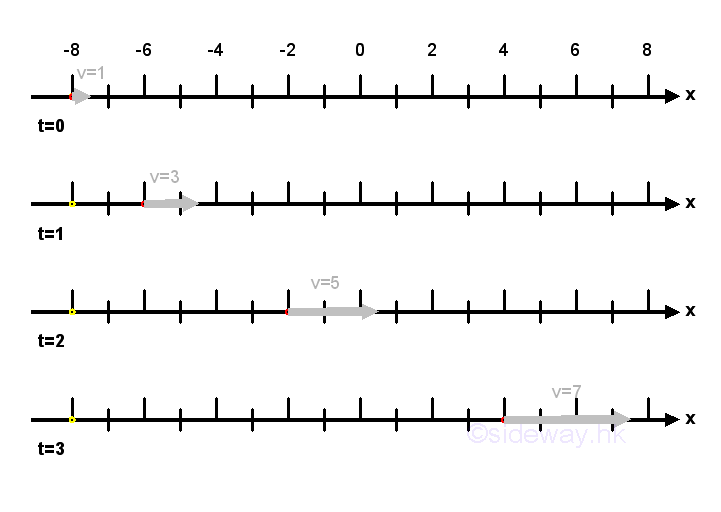

Similar to the position of the object, as the velocity of the object changes continuously, the change of velocity Δv in a time interval Δt can be expressed in term of a function of time t and Δt also, that is Δv=g(t+Δt)-g(t). By definition, acceleration of an object is equal to the rate of change of velocity v in a time interval. From calculus, by the definition of derivative, the rate of change of velocity with respect to time t when taking limit as Δt approaching 0 is equal to the derivative of the velocity function g(t) with respect to time t. In other words, acceleration is equal to the derivative of the velocity function, that is a=dv/dt=2. Imply

The acceleration of the object is therefore can be obtained from the velocity function g(t) and be expressed as a function of time, that is a=h(t)=2. Imply velocity can be determined by the acceleration function h(t) directly.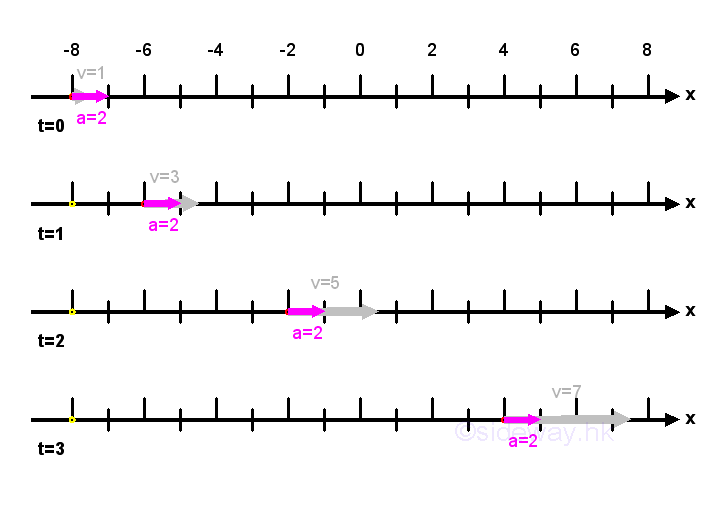

Velocity as a function of time

If the velocity of an object can be expressed in term of a function of time, g(t), the velocity of the object can be determined by time t. For example v=g(t)=1+2t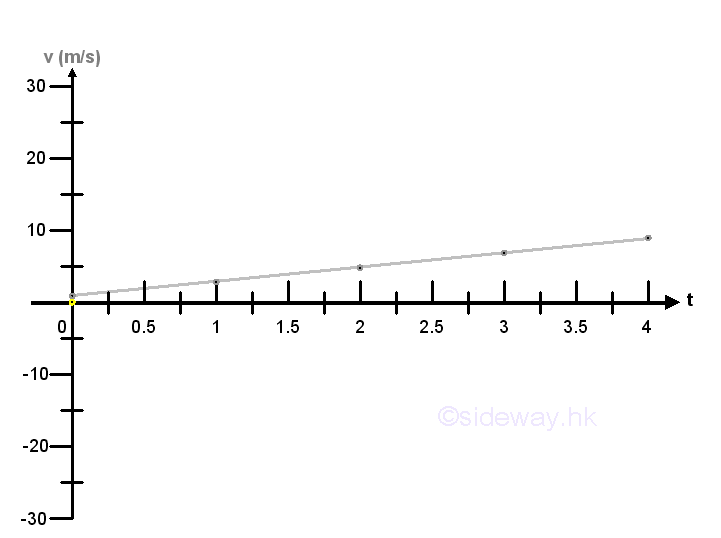

Since the velocity of the object changes continuously, the velocity change Δv in a time interval Δt can be expressed in term of a function of time t and Δt also, that is Δv=g(t+Δt)-g(t). By definition, acceleration of an object is equal to the rate of change of velocity v in a time interval. From calculus, by the definition of derivative, the rate of change of velocity v with respect to time t when taking limit as Δt approaching 0 is equal to the derivative of the velocity function g(t) with respect to time t. In other words, acceleration is equal to the derivative of the velocity function, that is a=dv/dt=2. Imply

The acceleration of the object can therefore be obtained from the velocity function g(t) and be expressed as a function of time, that is a=h(t)=2. Imply acceleration can be determined by the acceleration function h(t) directly.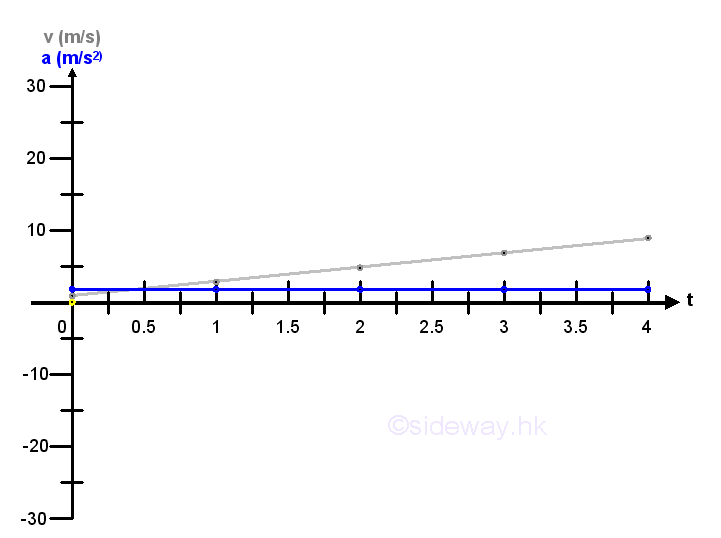

Since the velocity of object changes continuously, the object moves continuously also. By definition, velocity of an object is equal to the rate of displacement or change of position x in a time interval. In other words,  the displacement Δx in a time interval Δt can be expressed in term of a function of time t and Δt also, that is Δx=f(t+Δt)-f(t)=vΔt=g(t)Δt. From calculus, by the definition of integral, the product of the velocity v at time t and the time interval Δt when taking limit as Δt approaching 0 is equal to the instantaneous displacement at time t. In other words, total displacement is equal to the integral of the velocity function, that is Δt→0⇒∑(Δx)=∫dx=∑(vΔt)=∫vdt=t+t2. And therefore the position of the object depends on the initial position of the object at time equal to zero or other reference position x=f(t) at the corresponding time t. Imply

The position of the object can therefore be obtained from the velocity function g(t) also if a reference condition is known before and be expressed as a function of time, that is x=f(t)=-8+t+t2. Imply position can be determined by the position function f(t) directly.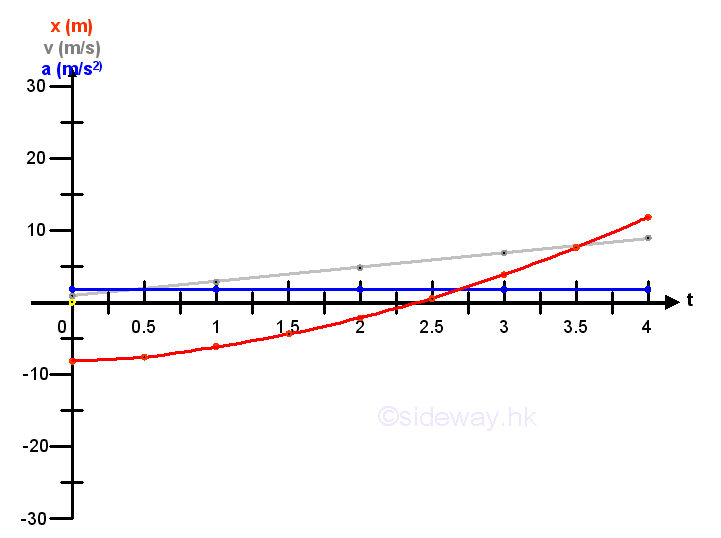

Acceleration as a function of time

If the acceleration of an object can be expressed in term of a function of time, h(t), the acceleration of the object can be determined by time t. For example a=h(t)=2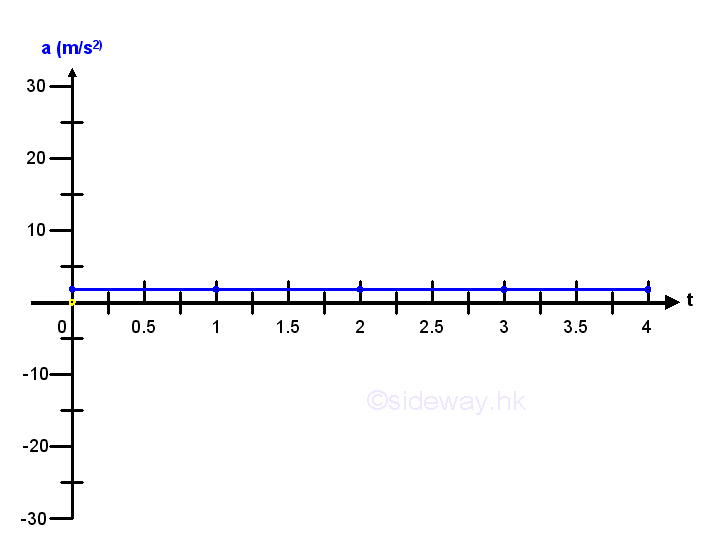

Since the acceleration of object changes continuously, the object moves continuously also. By definition, acceleration of an object is equal to the rate of velocity change in a time interval. In other words,  the velocity change Δv in a time interval Δt can be expressed in term of a function of time t and Δt also, that is Δv=g(t+Δt)-g(t)=aΔt=h(t)Δt. From calculus, by the definition of integral, the product of the acceleration a at time t and the time interval Δt when taking limit as Δt approaching 0 is equal to the instantaneous velocity change at time t. In other words, total velocity change is equal to the integral of the acceleration function, that is Δt→0⇒∑(Δv)=∫dv=∑(aΔt)=∫adt=2t. And therefore the velocity of the object depends on the initial velocity of the object at time equal to zero or other reference velocity v=g(t) at the corresponding time t. Imply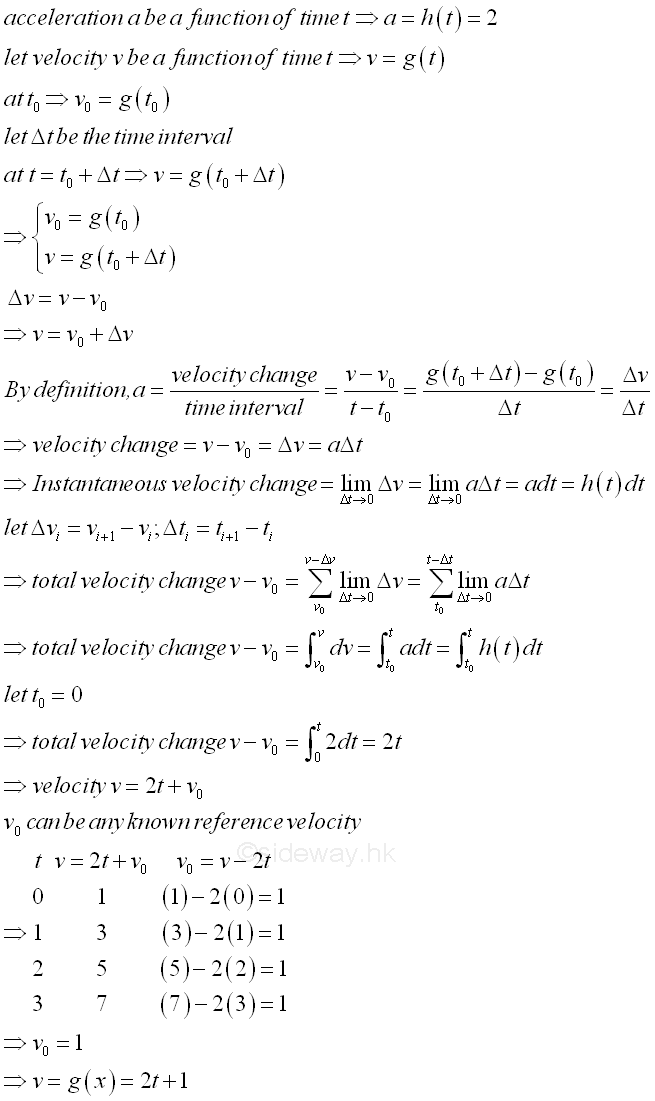

The velocity of the object can therefore be obtained from the acceleration function h(t) if a reference condition is known before and be expressed as a function of time, that is v=g(t)=1+2t. Imply velocity can be determined by the velocity function g(t) directly.

Similarly, the position of the object can therefore be obtained from the velocity function g(t) also if a reference condition is known before and be expressed as a function of time, that is x=f(t)=-8+t+t2 as before. Imply position can be determined by the position function f(t) directly.

However, if there is no reference condition is known for the velocity, the initial velocity is an unknown constant, that is v=g(t)=2t+v0. And the position function of the object from the velocity of the object becomes an equation with two unknown. Therefore two reference conditions are needed for determining the two unknown constants by setting up two equations. Imply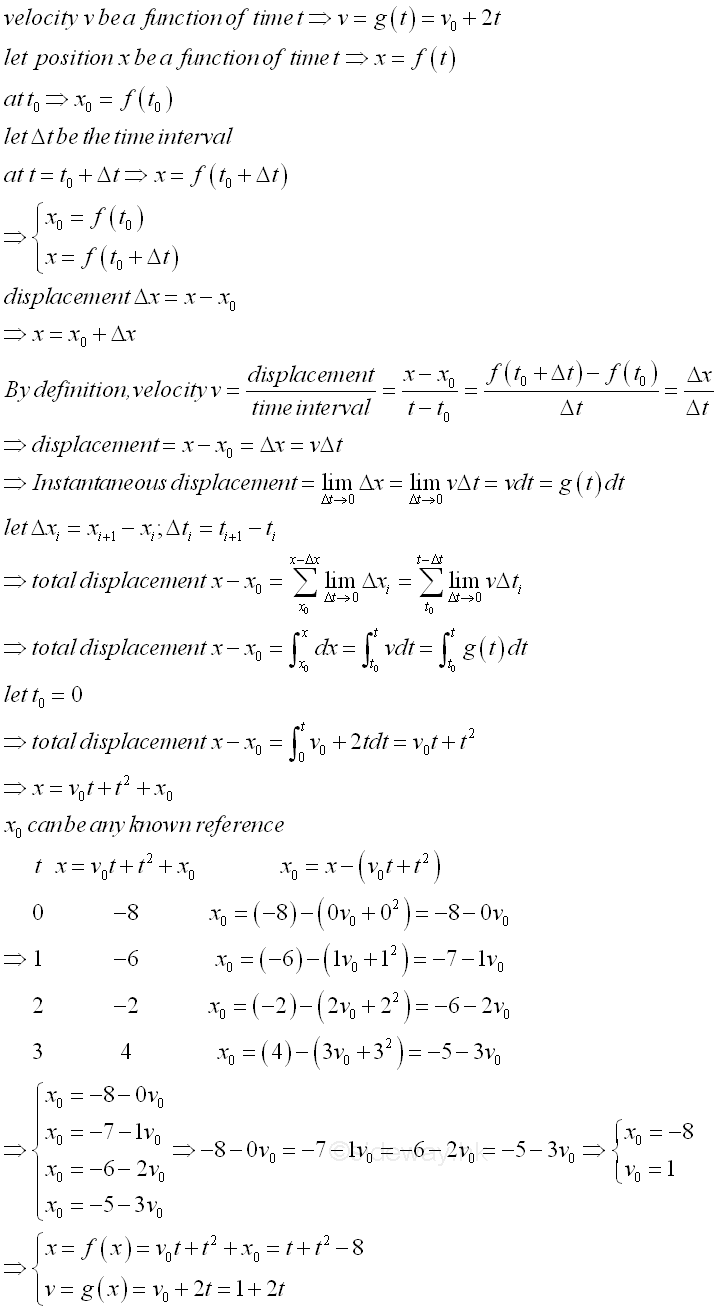

Imply velocity and position of the object can be obtained directly by the velocity function g(t) and position function f(t) accordingly.

 

Example 1

An object falls from a x m high cliff with initial speed v1m/s downward. Air resistance may be ignored, so the object is in free fall. For free fall, the acceleration can be assumed to be equal to a=9.8m/s2 downward. What is the speed and distance travel after t s? And what is the velocity of the object when touching the ground? Both the velocity and position of the object can be expressed as a function in term of time t. Imply