 Sideway
BICK BLOG from Sideway
Sideway
BICK BLOG from Sideway
|
Link:http://output.to/sideway/default.asp?qno=120600013 Centroid of 3D Body Centroid of 3D BodyThe centroid of 3D Body is determined by the first moment of a three dimensional body with the method of the first moment of volume. 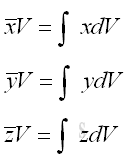
Centroids of VolumesVolume by IntegrationAlthough triple integration is usually required to determine the volume of 3D body. However volume of 3D body can also be determined by performing a double integration or a single integration. Volume by Double IntegrationIf the inner integration of the unit elemental volume can be expressed as a strip of elemental volume in one dimension. 
For example, the signed volume of the 3D ellipic cylinder is bounded by surfaces in rectangular form , Imply 
An elemental volume ΔV in rectangular form can be defined as Δx times Δy times Δz. Imply 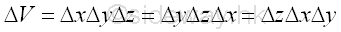
An unit elemental volume can be expressed as 
Therefore the unit elemental volume can be expressed as a strip of elemental volume of the solid cylinder U in the planar region R of cartesian coordinates yz. Imply 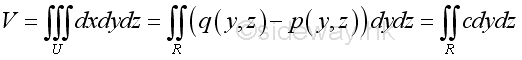
All unit elemental volumes can be bounded by curves in the plane yz. And the curves is 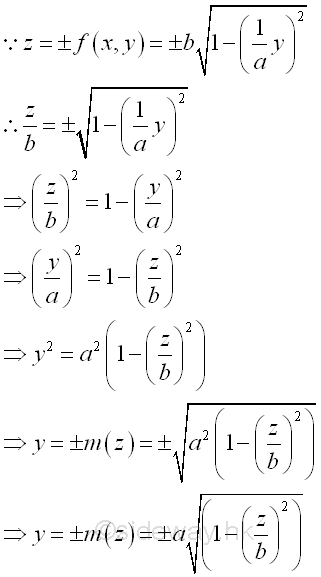
In general, the volume of a region can be determined by double integration through sweeping the signed elemental volume starting from along either rectangular coordinate axes. Imply Starting from horizontal sweeping along y axis 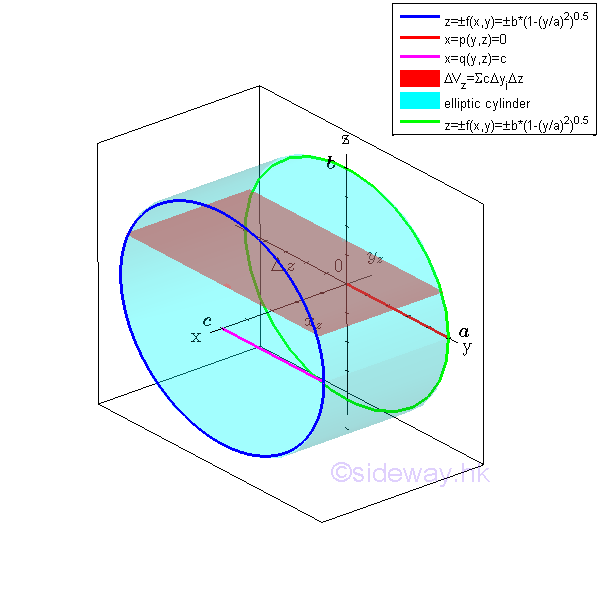
Consider an unit elemental volume ΔVyz along y axis horizontally. Imply 
Since the bounding curves are joined at plane zx, The bounds of the bounding curves are 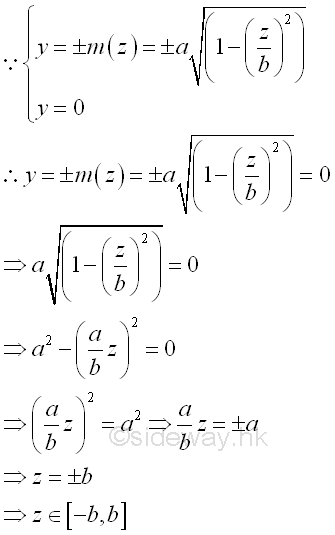
Therefore the volume of the solid cone U can be determined by 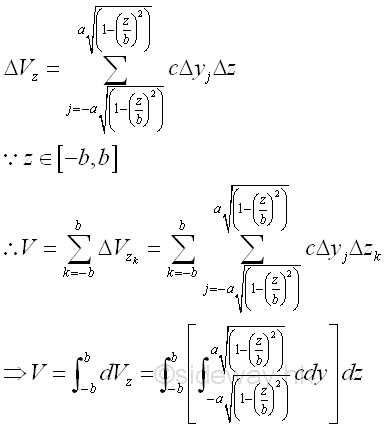
Therefore the volume of the solid cone U is 
Volume by Single IntegrationIf the inner integration of the unit elemental volume can be expressed as a sheet of elemental volume in two dimensions. 
For example, the signed volume of the 3D ellipic cylinder is bounded by surfaces in rectangular form , Imply 
An elemental volume ΔV in rectangular form can be defined as Δx times Δy times Δz. Imply 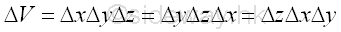
An unit elemental volume can be expressed as 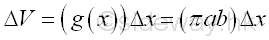
Therefore the unit elemental volume can also be expressed as a sheet of elemental volume of the solid cylinder U along the cartesian coordinate axis x. Imply 
Sweeping the unit elemental volume ΔVx along x axis horizontally Since all unit elemental volumes of ΔVx are bounded along x axis, imply 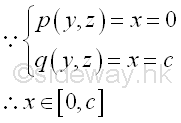
Therefore the volume of the solid cone U is 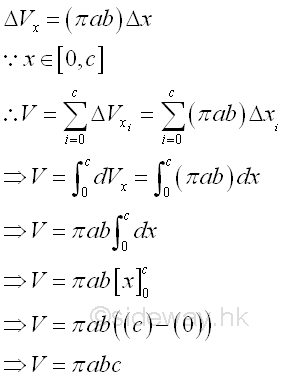
Link:http://output.to/sideway/default.asp?qno=120600011 Centroid of 3D Body Centroid of 3D BodyThe centroid of 3D Body is determined by the first moment of a three dimensional body with the method of the first moment of volume. 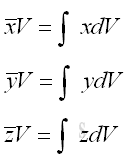
Centroids of VolumesVolume by IntegrationVolume by Triple Integration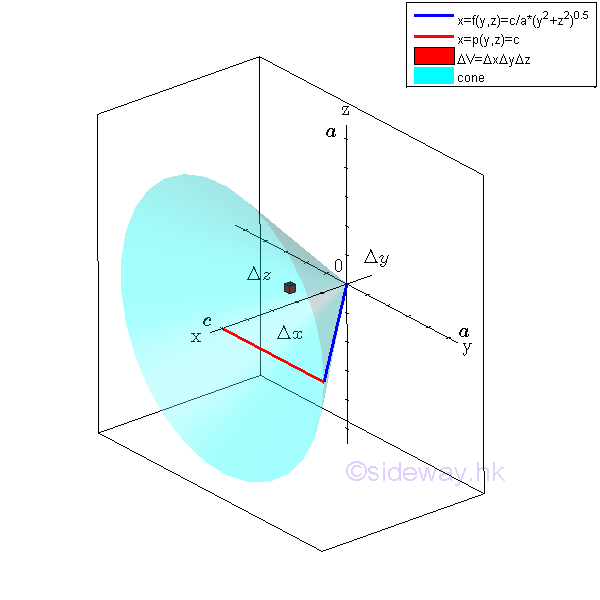
For example, the signed volume of the 3D region U is bounded by surfaces in rectangular form , Imply 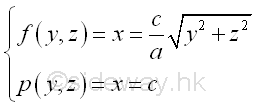
An elemental volume ΔV in rectangular form can be defined as Δx times Δy times Gz. Imply 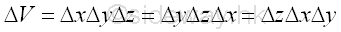
Therefore the volume of the solid cone U in cartesian coordinates xyz is equal to 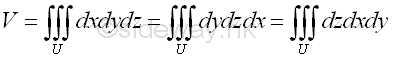
In general, the volume of a region can be determined by multiple integration through sweeping the signed elemental volume starting from along any one of the rectangular coordinate axes. Imply Starting from horizontal sweeping along x axis 
Considering an elemental volume along x axis. Imply 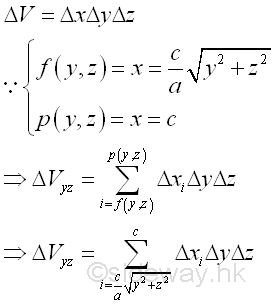
All elemental volumes can be bounded by curves in the plane yz. And the curves is 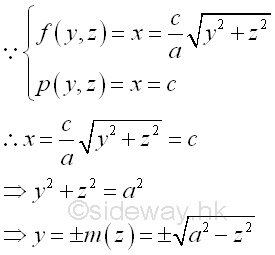
Similarly sweeping the elemental volume ΔVyz along y axis horizontally. 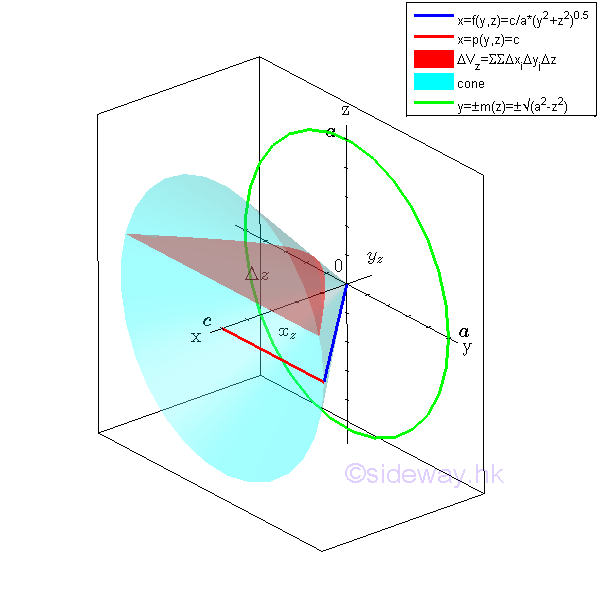
Considering an elemental volume ΔVz along y axis. Imply 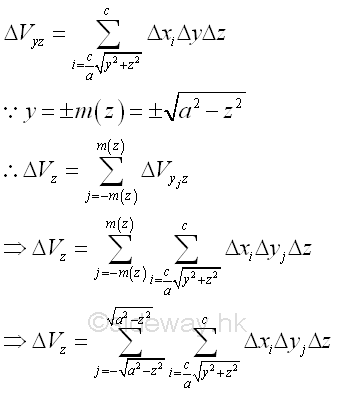
Since the bounding curves are joined at plane zx, The bounds of the bounding curves are 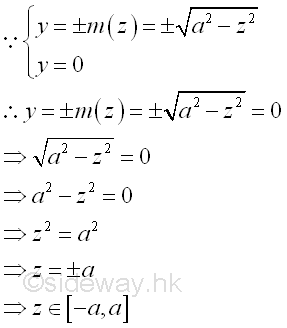
Therefore the volume of the solid cone U is 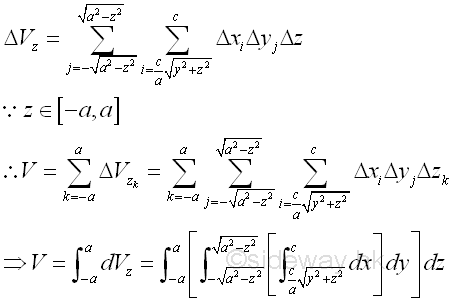
The volume of the solid cone U can also be determined starting from other axis. Starting from horizontal sweeping along y axis 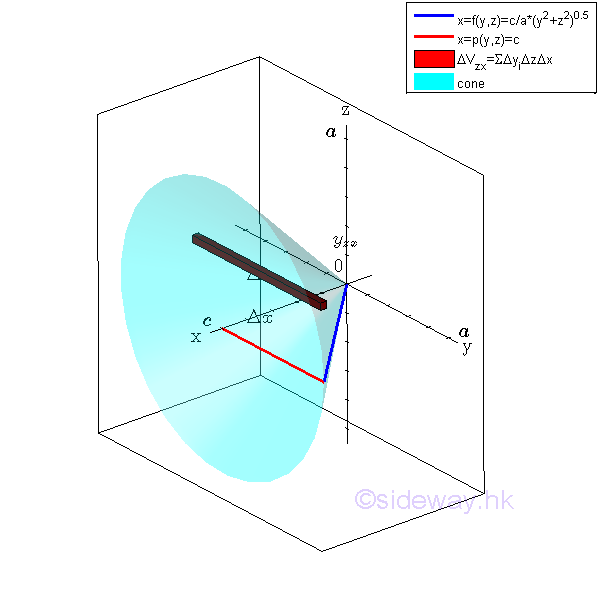
Considering an elemental volume along y axis. Imply 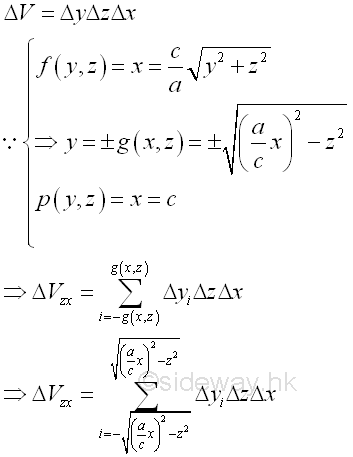
All elemental volumes in z direction can be bounded by curves in the plane zx. And the curves is 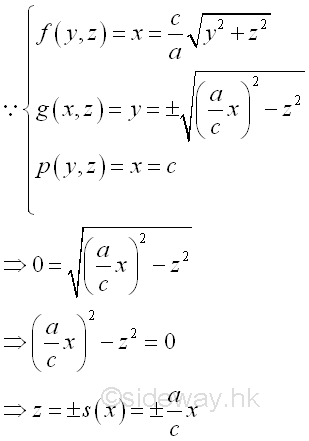
Similarly sweeping the elemental volume ΔVzx along z axis vertically. 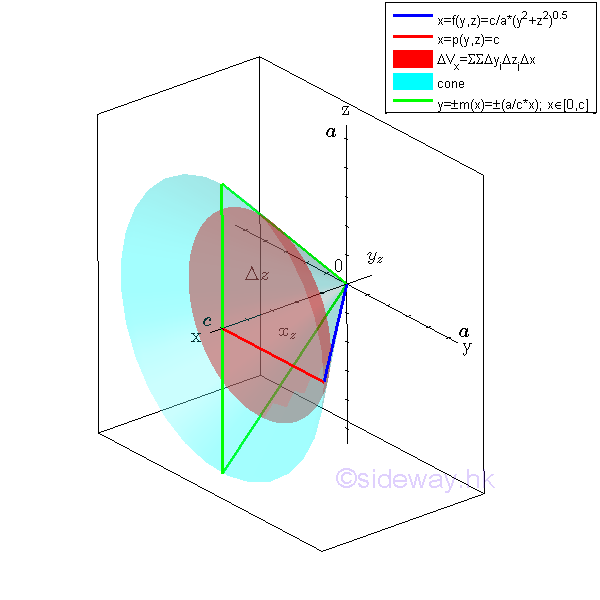
Considering an elemental volume ΔVx along z axis. Imply 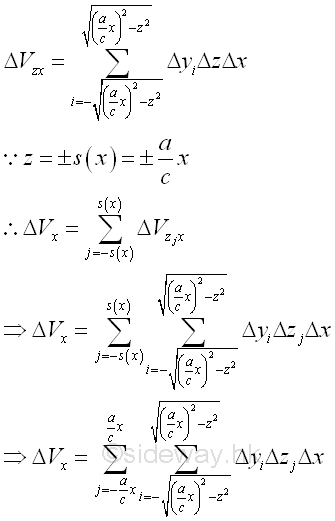
The bounding curves in x direction can also be bounded at plane zx. The bounds of the bounding curves are 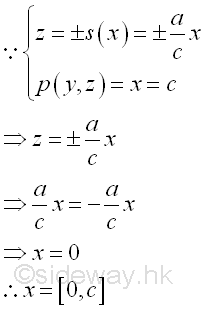
The volume of the solid cone U can be expressed as 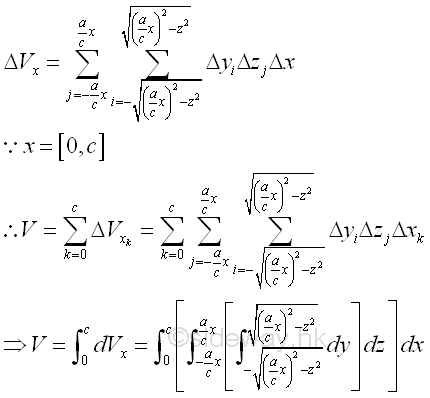
Therefore the volume of the solid cone U is 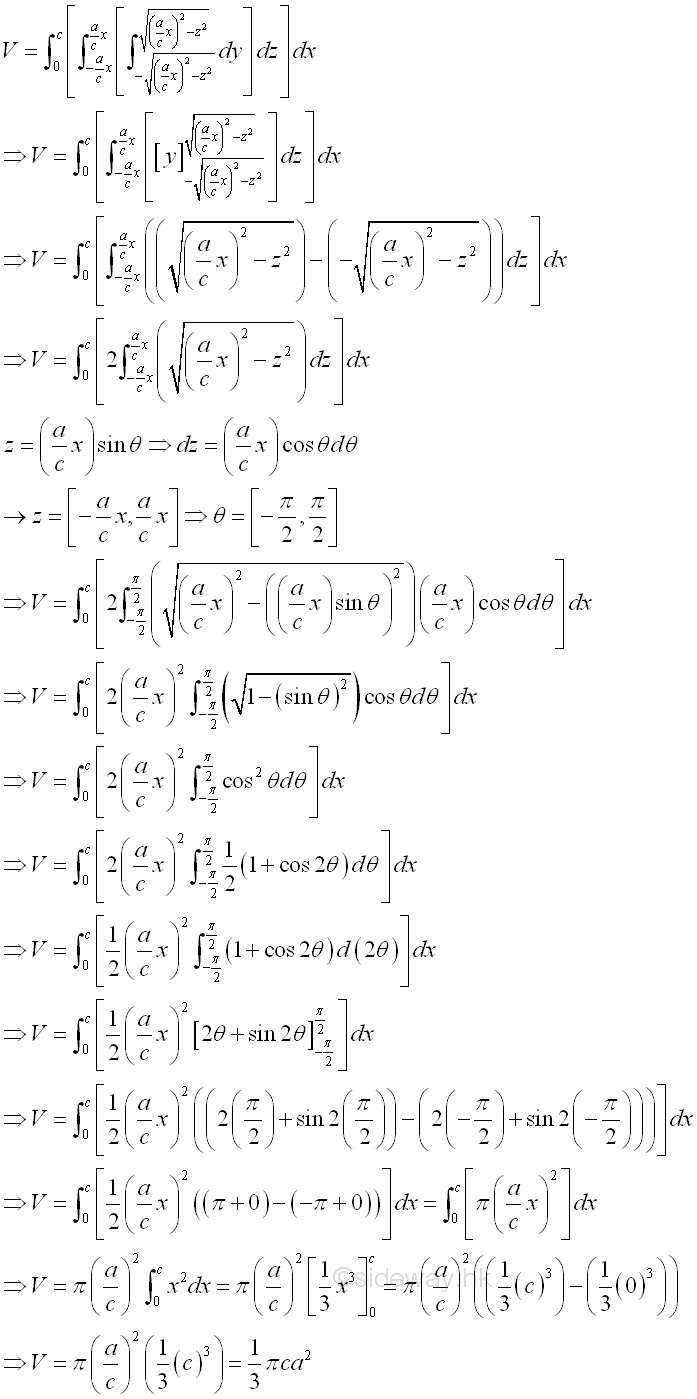
|
Sideway BICK Blog 18/06 |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||

