 Sideway
BICK BLOG from Sideway
Sideway
BICK BLOG from Sideway
|
Link:http://output.to/sideway/default.asp?qno=120600003 Centroid of Plane Body Centroid of 2D Plane BodyThe centroid of an plate is determined by the first moment of a two dimensional plane body with the method of the first moment of area. 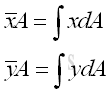
And the centroid of a wire is determined by the first moment of a two dimensional plane body with the method of the first moment of line. 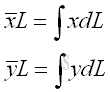
Centroids of AreasArea by IntegrationAlthough double integration is usually required to determine the planar area. However a planar area can also be determined by performing a single integration. If the inner integration of the unit elemental area is a thin elemental area. Area by Single Integration
For example, the signed area of the planar region R is bounded by curves in rectangular form , Imply 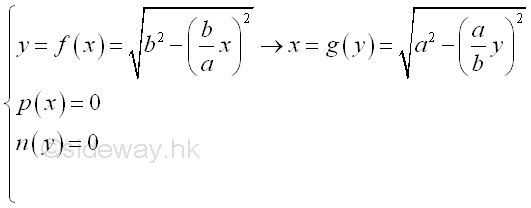
An unit elemental area ΔA in rectangular form can be defined as Δx times Δy. Imply 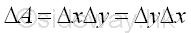
In general, the unit element area of a region can be extended to either a thin vertical rectangular strip or a thin horizontal rectangular strip. And the element area ΔA becomes 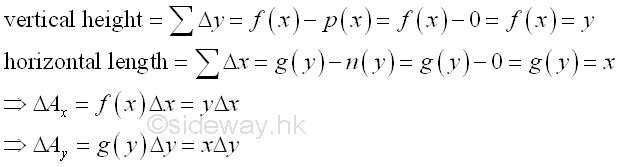
By using a thin rectangular strip as the element area or applying the method of strip slicing, the signed area of the planar region can be determined by a single integration through sweeping the signed elemental area strip along either rectangular coordinate axis. Imply By sweeping the horizontal strip along y axis vertically 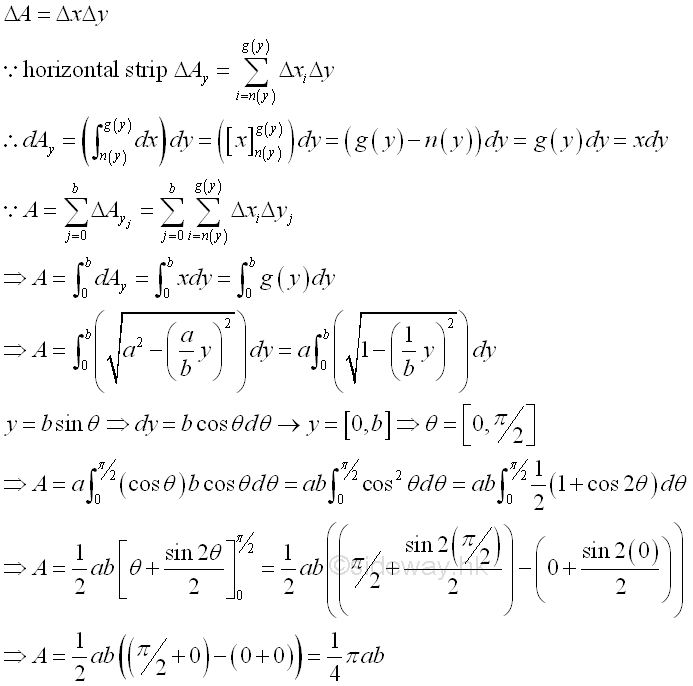
By sweeping the vertical strip along x axis horizontally 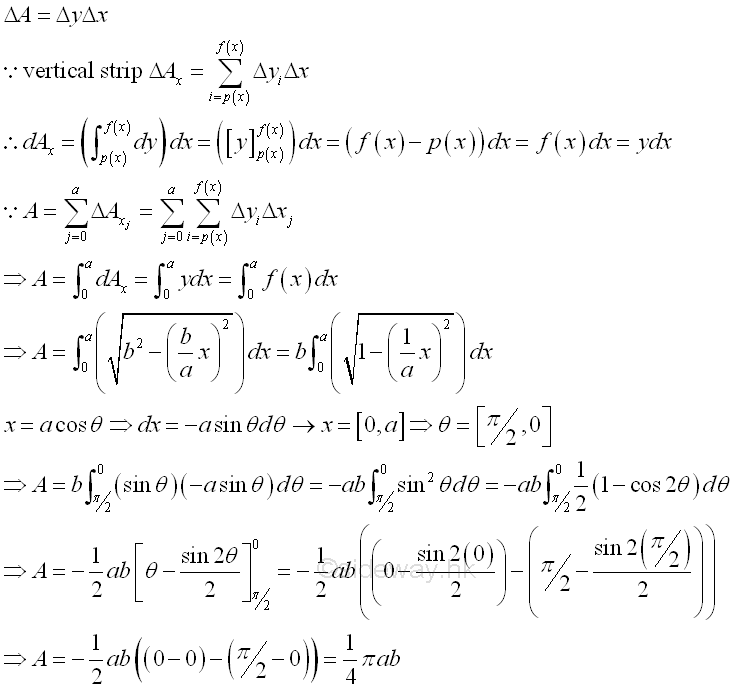
And for curves in polar form 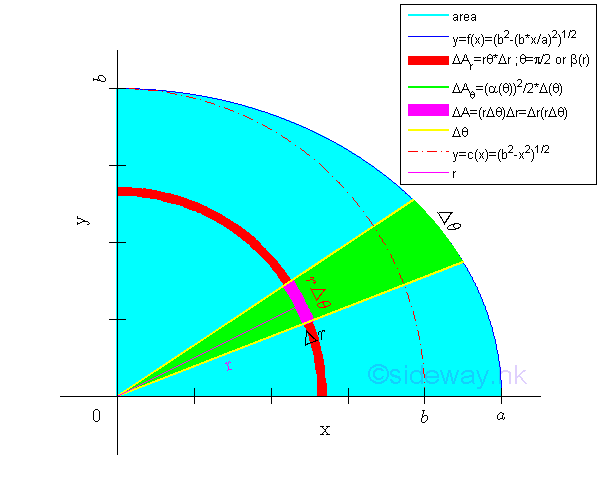
For example, the signed area of the planar region R is bounded by curves in polar form, Imply 
An unit elemental area ΔA in polar form can be approximated by Δr times rΔθ. Imply 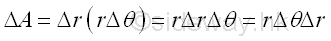
In general, the unit element area of a region can be extended to either a thin slice of circular sector or a thin circular arc strip. And the element area ΔA becomes. 
By using a thin circular arc strip as the element area and sweeping radically, or using a thin slice of circular sector as the element area and sweeping circularly, the signed area of the planar region can be determined by a single integration through sweeping the signed elemental area starting from along either polar variables. Imply By sweeping the thin circular sector slice along variable angle θ circularly 
By sweeping the thin circular arc strip along variable radius r radically , 
|
Sideway BICK Blog 02/06 |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||

