 Sideway
BICK BLOG from Sideway
Sideway
BICK BLOG from Sideway
|
Link:http://output.to/sideway/default.asp?qno=120600006 Centroid of Plane Body Centroid of 2D Plane BodyThe centroid of an plate is determined by the first moment of a two dimensional plane body with the method of the first moment of area. 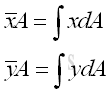
And the centroid of a wire is determined by the first moment of a two dimensional plane body with the method of the first moment of line. 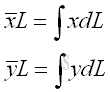
Centroids of LinesCurve Length of Quarter-Circular Arc by Integration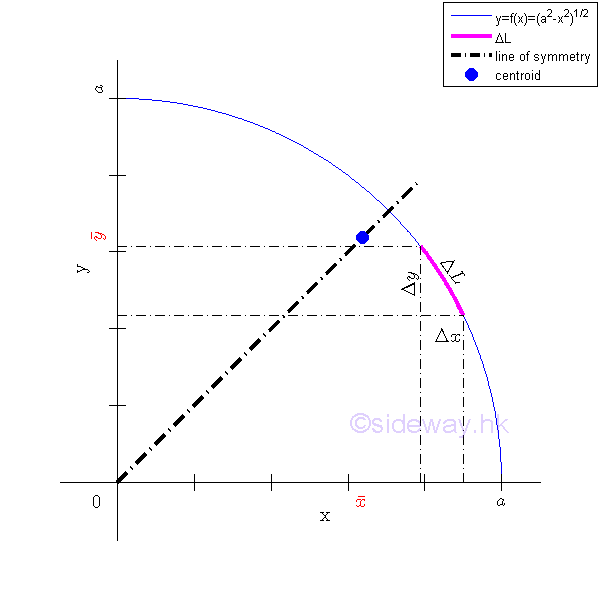
For example, the curve segment bounded by curves in rectangular form , Imply 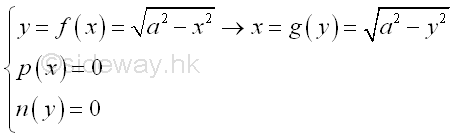
An elemental curve fragment ΔL in rectangular form can be approximated by pythagorean theorem. Imply 
By taking the limit, the dimension of the curve element can be expressed as 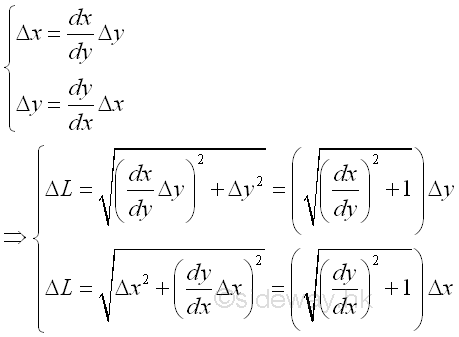
In general, the length of the curce in a region can be determined by integration through sweeping the curve element along either rectangular coordinate axis. Imply Sweeping along x axis horizontally 
The length of the curce in a region can also be determined by integration through sweeping the curve element along y axis in similar way. Centroid of Quarter-Circular Arc by IntegrationThe centroid of the planar curve can be determined by a single integration through sweeping the elemental centroid of the curve fragment along either rectangular coordinate axis. 
Sweeping along y axis vertically The x coordinate of centroid of the planar curve is. 
The y coordinate of centroid of the planar curve is. 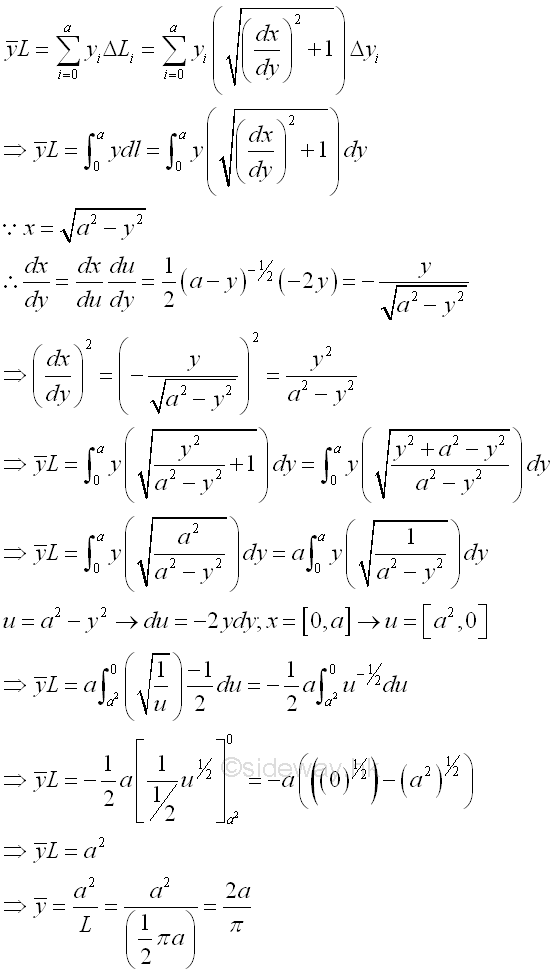
Centroid of Semi-Circular Arc by Integration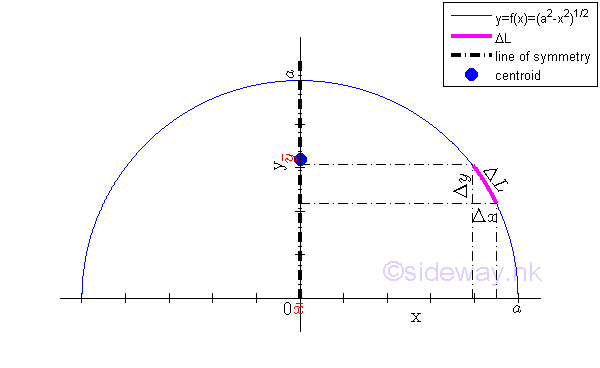
For example, the curve segment bounded by curve in rectangular form , Imply 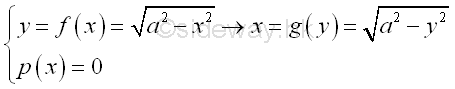
By symmetry, the length of a semi-circular arc is 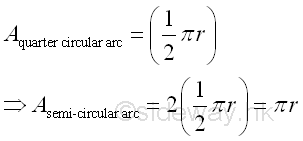
The centroid of the planar curve can be determined by a single integration through sweeping the elemental centroid of the curve fragment along either rectangular coordinate axis. 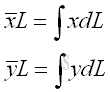
Sweeping along x axis horizonatally Coordinate x of centroid by symmetry. 
Coordinate x of centroid by integration. 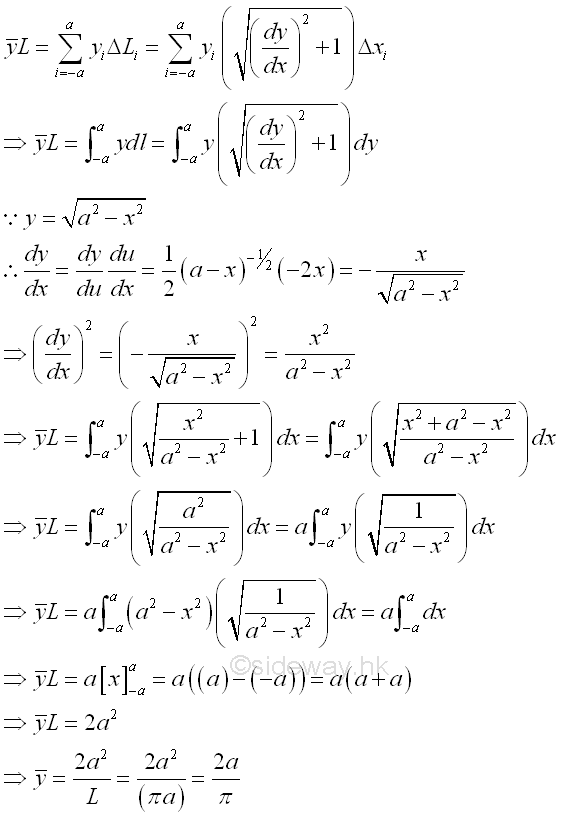
Centroid of Circular Arc by Integration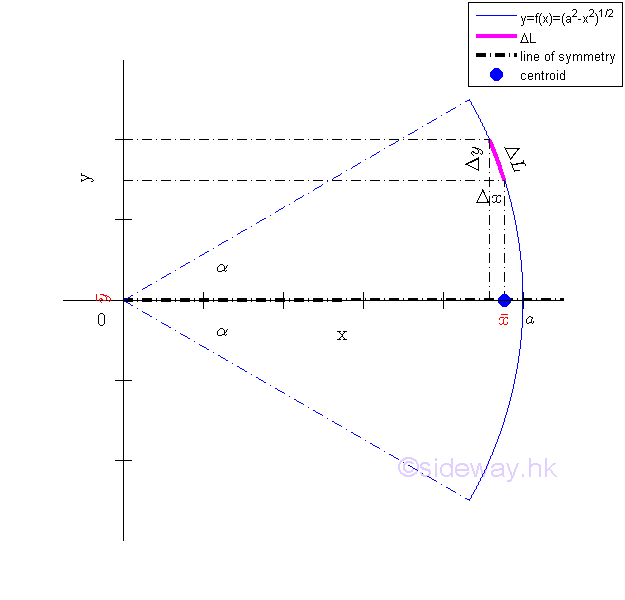
For example, the curve segment bounded by curve in polar form , Imply 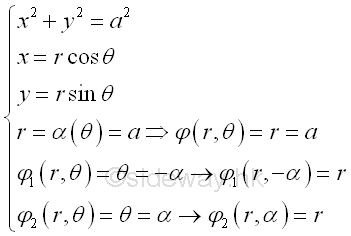
The length of the curve segment 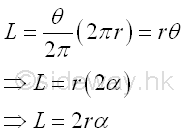
The centroid of the planar curve can be determined by a single integration through sweeping the elemental centroid of the curve fragment along variable angle c circularly. 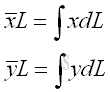
By sweeping the centroid of circular sector slice along variable angle θ circularly Coordinate x of centroid by integration. Imply 
Coordinate y of centroid by symmetry. Imply 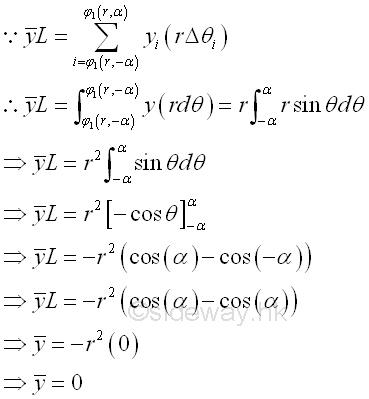
|
Sideway BICK Blog 07/06 |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||

