|
Link:http://output.to/sideway/default.asp?qno=160900024 Euclid's Elements Book 7
The Euclid's Elements of Geometry
Geometry is the study of figures. Euclid's Elements provides the
most fundamental way of learning geometry geometrically. based on
Book VII: Fundamentals of number theory
.
Definitions
.
-
A unit is that by virtue of which each of the things that exist is called one.
-
A number is a multitude composed of units.
-
A number is a part of a number, the less of the greater, when it measures the
greater;
-
But parts when it does not measure it.
-
The greater number is a multiple of the less when it is measured by the less.
-
An even number is that which is divisible into two equal parts.
-
An odd number is that which is not divisible into two equal parts, or that which
differs by a unit from an even number.
-
An even-times-even number is that which is measured by an even number according
to an even number.
-
An even-times-odd number is that which is measured by an even number according
to an odd number.
-
An odd-times-odd number is that which is measured by an odd number according to
an odd number.
-
A prime number is that which is measured by a unit alone.
-
Numbers relatively prime are those which are measured by a unit alone as a
common measure.
-
A composite number is that which is measured by some number.
-
Numbers relatively composite are those which are measured by some number as a
common measure.
-
A number is said to multiply a number when the latter is added as many times as
there are units in the former.
-
And, when two numbers having multiplied one another make some number, the number
so produced be called plane, and its sides are the numbers which have multiplied
one another.
-
And, when three numbers having multiplied one another make some number, the
number so produced be called solid, and its sides are the numbers which have
multiplied one another.
-
A square number is equal multiplied by equal, or a number which is contained by
two equal numbers.
-
And a cube is equal multiplied by equal and again by equal, or a number which is
contained by three equal numbers.
-
Numbers are proportional when the first is the same multiple, or the same part,
or the same parts, of the second that the third is of the fourth.
-
Similar plane and solid numbers are those which have their sides proportional.
-
A perfect number is that which is equal to the sum its own parts.
Propositions
-
When two unequal numbers are set out, and the less is continually subtracted in turn from the
greater, if the number which is left never measures the one before it until a
unit is left, then the original numbers are relatively prime.
-
To find the greatest common measure of two given numbers not relatively prime.
Corollary: If a number measures two numbers, then it also measures their
greatest common measure.
-
To find the greatest common measure of three given numbers not relatively prime.
-
Any number is either a part or parts of any number, the less of the greater.
-
If a number is part of a number, and another is the same part of another, then
the sum is also the same part of the sum that the one is of the one.
-
If a number is parts of a number, and another is the same parts of another, then
the sum is also the same parts of the sum that the one is of the one.
-
If a number is that part of a number which a subtracted number is of a
subtracted number, then the remainder is also the same part of the remainder
that the whole is of the whole.
-
If a number is the same parts of a number that a subtracted number is of a
subtracted number, then the remainder is also the same parts of the remainder
that the whole is of the whole.
-
If a number is a part of a number, and another is the same part of another, then
alternately, whatever part or parts the first is of the third, the same part, or
the same parts, the second is of the fourth.
-
If a number is a parts of a number, and another is the same parts of another,
then alternately, whatever part of parts the first is of the third, the same
part, or the same parts, the second is of the fourth.
-
If a whole is to a whole as a subtracted number is to a subtracted number, then
the remainder is to the remainder as the whole is to the whole.
-
If any number of numbers are proportional, then one of the antecedents is to one
of the consequents as the sum of the antecedents is to the sum of the
consequents.
-
If four numbers are proportional, then they are also proportional alternately.
-
If there are any number of numbers, and others equal to them in multitude, which
taken two and two together are in the same ratio, then they are also in the same
ratio ex aequali.
-
If a unit number measures any number, and another number measures any other
number the same number of times, then alternately, the unit measures the third
number the same number of times that the second measures the fourth.
-
If two numbers multiplied by one another make certain numbers, then the numbers
so produced equal one another.
-
If a number multiplied by two numbers makes certain numbers, then the numbers so
produced have the same ratio as the numbers multiplied.
-
If two number multiplied by any number make certain numbers, then the numbers so
produced have the same ratio as the multipliers.
-
If four numbers are proportional, then the number produced from the first and
fourth equals the number produced from the second and third; and, if the number
produced from the first and fourth equals that produced from the second and
third, then the four numbers are proportional.
-
The least numbers of those which have the same ratio with them measure those
which have the same ratio with them the same number of times; the greater the
greater; and the less the less.
-
Numbers relatively prime are the least of those which have the same ratio with
them.
-
The least numbers of those which have the same ratio with them are relatively
prime.
-
If two numbers are relatively prime, then any number which measures one of them
is relatively prime to the remaining number.
-
If two numbers are relatively prime to any number, then their product is also
relatively prime to the same.
-
If two numbers are relatively prime, then the product of one of them with itself
is relatively prime to the remaining one.
-
If two numbers are relatively prime to two numbers, both to each, then their
products are also relatively prime.
-
If two numbers are relatively prime, and each multiplied by itself makes a
certain number, then the products are relatively prime; and, if the original
numbers multiplied by the products make certain numbers, then the latter are
also relatively prime.
-
If two numbers are relatively prime, then their sum is also prime to each of
them; and, if the sum of two numbers is relatively prime to either of them, then
the original numbers are also relatively prime.
-
Any prime number is relatively prime to any number which it does not measure.
-
If two numbers, multiplied by one another make some number, and any prime number
measures the product, then it also measures one of the original numbers.
-
Any composite number is measured by some prime number.
-
Any number is either prime or is measured by some prime number.
-
Given as many numbers as we please, to find the least of those which have the
same ratio with them.
-
To find the least number which two given numbers measure.
-
If two numbers measure any number, then the least number measured by them also
measures the same.
-
To find the least number which three given numbers measure.
-
If a number is measured by any number, then the number which is measured has a
part called by the same name as the measuring number.
-
If a number has any part whatever, then it is measured by a number called by the
same name as the part.
-
To find the number which is the least that has given parts.
Link:http://output.to/sideway/default.asp?qno=160900025 Broadcom BCM57780
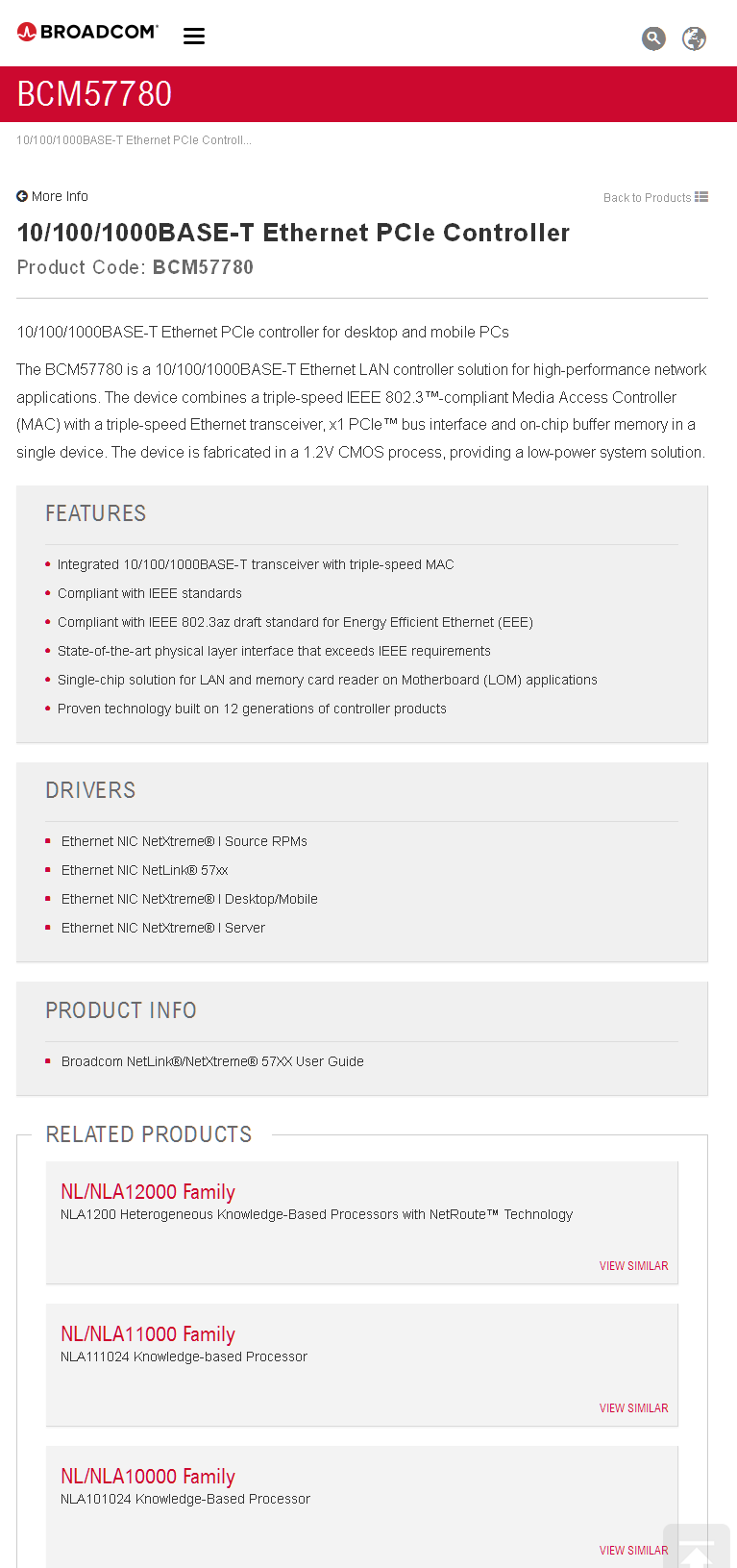
Broadcom BCM57780
(information from www.broadcom.com )
last updated 17Sep2016
The BCM57780 is a 10/100/1000BASE-T
Ethernet LAN controller solution for high-performance network applications. The
device combines a triple-speed IEEE 802.3™-compliant Media Access Controller
(MAC) with a triple-speed Ethernet transceiver, x1 PCIe™ bus interface and
on-chip buffer memory in a single device.
Features:
- Integrated 10/100/1000BASE-T transceiver with triple-speed MAC
- Compliant with IEEE standards
- Compliant with IEEE 802.3az draft standard for Energy Efficient Ethernet (EEE)
- State-of-the-art physical layer interface that exceeds IEEE requirements
- Single-chip solution for LAN and memory card reader on Motherboard (LOM)
applications
- Proven technology built on 12 generations of controller products
Site of broadcom - Broadcom Ltd. | Analog and digital semiconductor solutions for the wired infrastructure, wireless communications, enterprise storage and industrial markets http://www.broadcom.com/ last updated 9/15/2016
|
|
 Sideway
BICK BLOG from Sideway
Sideway
BICK BLOG from Sideway