Sideway
BICK BLOG from Sideway
Sideway
BICK BLOG from Sideway
|
Link:http://output.to/sideway/default.asp?qno=120400003 First Moment of Plane Body First Moment of 2D Plane BodyThe first moment of a two dimensional plane body is defined as the summation of the moments of all elements of the shape of the two dimensional plane body about an axis. The first moment of a two dimensional plane body is the mathematical measure of the distribution of the shape of a two dimensional plane body about an axis. The first moment of a two dimensional plane body can be used to detemine the centroid of the an object. The first moment of a two dimensional plane body is usually called the first moment of area and sometimes is misnamed as the first moment of inertia. 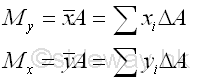
In practical problems, the centroid of an plate is determined by the first moment of a two dimensional plane body with the method of the first moment of area. 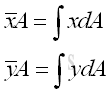
And the centroid of a wire is determined by the first moment of a two dimensional plane body with the method of the first moment of line. 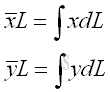
The first moment of area can also be used to determine the static moment of area, Q. The static moment of area is a propety to measure the moment of an area about an axis of the shape of a cross-section. The static moment of area is commonly used for determining the distribution of shear stress in flexural members under transverse loadings. 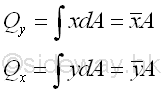
Centroidal AxisAlthough the value of first moment of an area is dependent on the reference axes due to the change of reference, the location of the centroid of an area is independent of the reference axes and is the property of the area only. 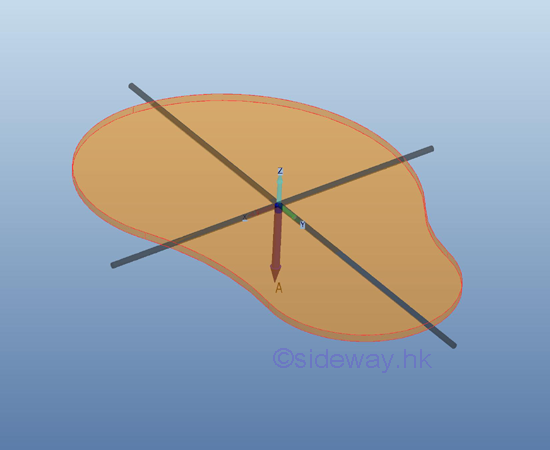
If the first moment of an area about an axis is equal to zero, the centroid of the area must be located on the axis. Conversely, if the centroid of an area is located on an axis, the first moment of the area must be equal to zero also. e.g. the axes x and y have their origin at the centroid. 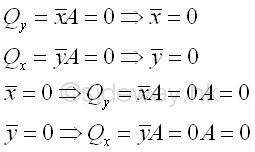
The axes pass through the centroid of an area are called centroidal axes. The first moments of area about any centroidal axis of the area are zero. Since the centroid is located on the centroidal axis, the perpendicular distance from the centroid to the centroidal axis must be zero also. Symmetry of Plane Body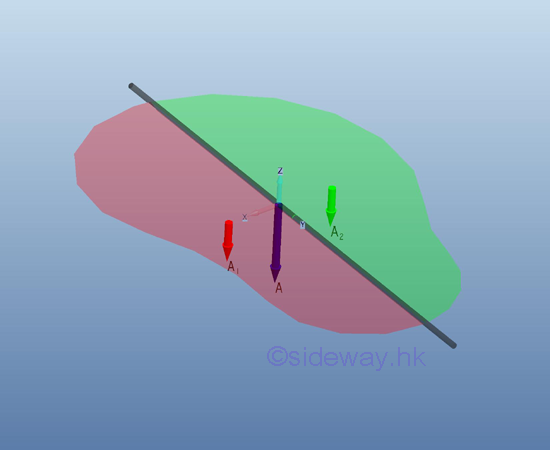
A centroidal axis always divide the plane body into two distinct subregions. Since the first moment of area of a plane body about its centroidal axis is equal to zero, the two first moment of area of the two distinct subregions about the centroidal axis of the plane body should be equal and opposite in sense. Imply 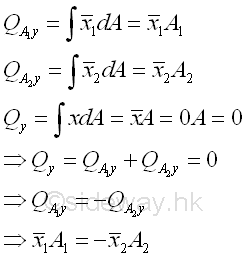
Considering the two subregions of a symmetrical plane body on either side of the axis of symmetry, the elemental areas are equal in size and are equidistant from the axis. For every elemental area on one side of the axis of symmetry, there alway exists an elemental area on the opposite side of the axis of symmetry. And the first moment of these elemental areas will cancel each other because the distances are equal and opposite in sense. Therefore the first moment of a symmetrical plane body about the axis of symmetry is equal to zero and the centroid of the symmetrical plane body should always lies on the symmetric axis also. 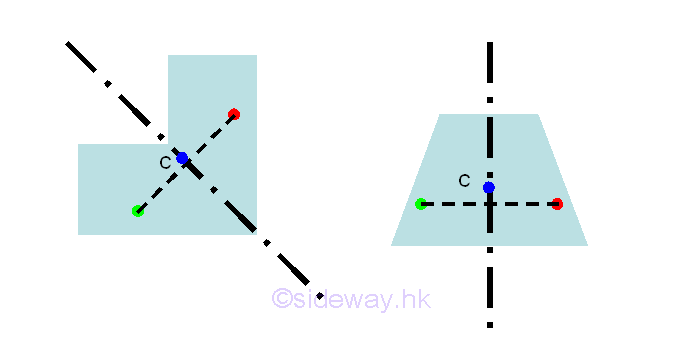
Since the centroid of a symmetrical plane body always lies on the symmetric axis, when a plane body possesses two or more axes of symmetry, the centroid of the plane body should always be located at the intersection of the axes. 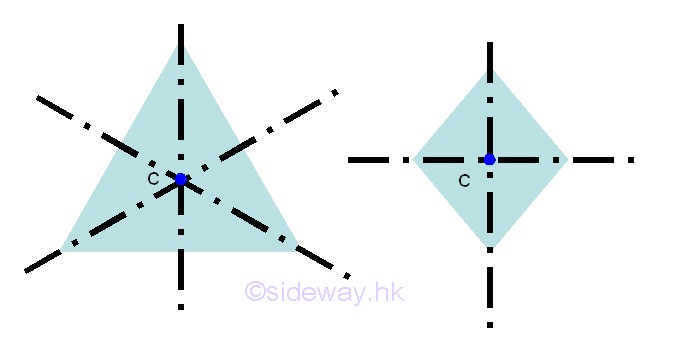
Similarly, the centroid of plane bodies with two or more axes of symmetry can be determined by the construction of axes of symmetry. e.g. 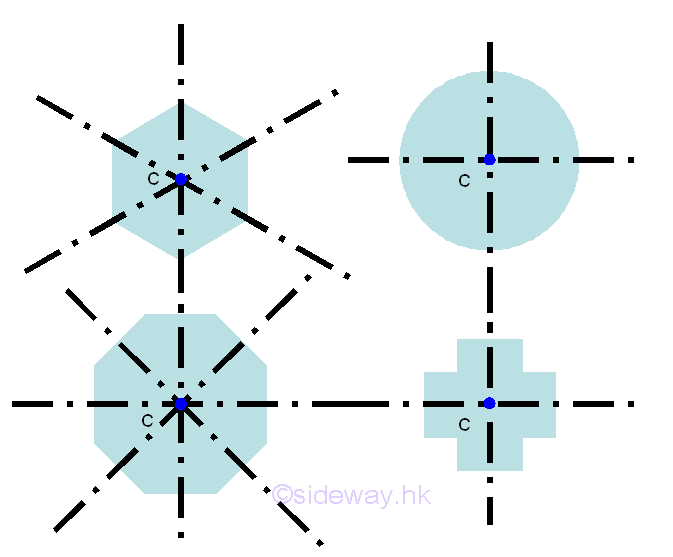
Besides the reflection symmetry, a symmetrical plane body can also be rotational symmetric about a point. Geometrically, for every element at coordinate x,y, there always exist an element at coordinate -x,-y. Therefore, a symmetrical plane body with two axes of symmetry at right angle to each other always symmetric about a point. From the above symmetry plane bodies, the centroids of the plane bodys always coincide with the center of symmetry, i.e. intersection of two axes. However, a rotational symmetric plane body sometime does not necessary to be symmetric about an axis. e.g. 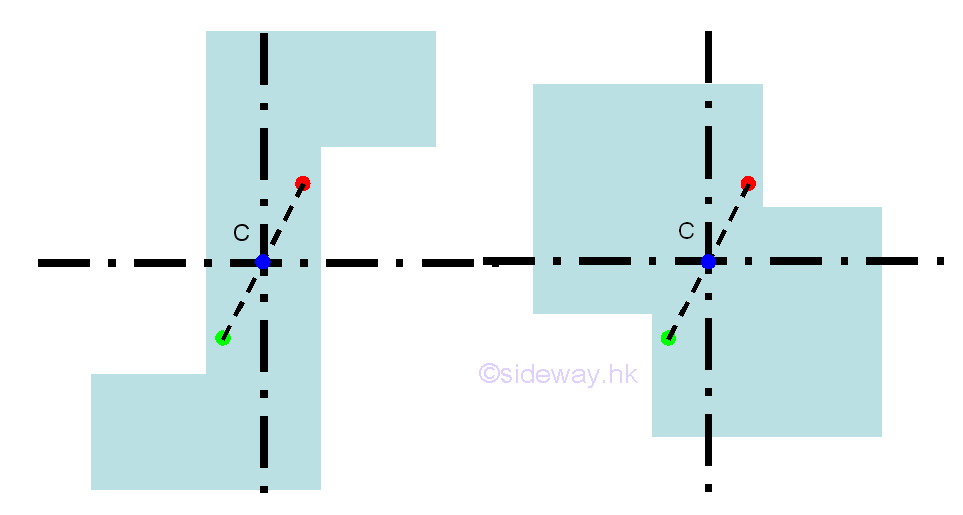
Link:http://output.to/sideway/default.asp?qno=120400002 Center of Gravity, Center of Mass, & Centroid Body Force of 2D Plane Body
When the thickness of a three dimensional body is small and uniform, the body can be condsidered as a plane body. The weight of the body is equal to the force exerted by the earth on the body. Center of Gravity of a Plane Plate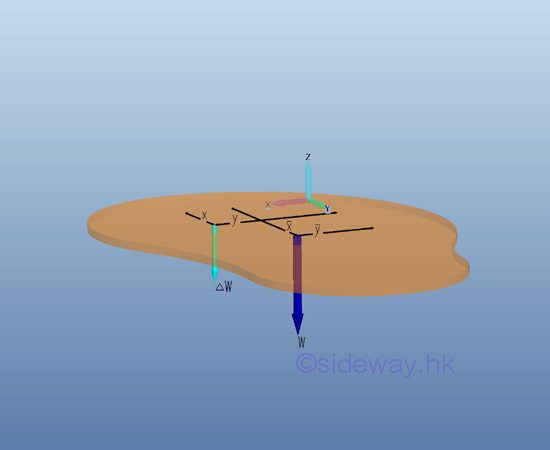
The force of gravity acts on each of the particles of the entire body. By dividing the plate into small finite regions or elements, the weight of the body can also be divided into small forces distributing over the plane plate. For a plane plate of n element, the weight of the plane plate is equal to 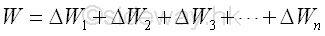
As in the equivalent systems of forces, two systems of forces are equivalent at the point of interest, if:
By assuming the forces exerted by the earth on the elements of plane plate are parallel, the resultant force is equal to a single force in the same direction. Therefore, the magnitude of the body force of the plane plate is 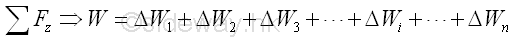
By denoting the position of the element of the plane plate relative to the coordinate system as xi,yi, the coordinates x , y of the center of gravity of the plane plate where the resultant force W applied can be determined by equating the moment of the resultant force W about the y and x axes and the corresponding mements of elements of the plane plate about the coordinate axis respectively. Imply 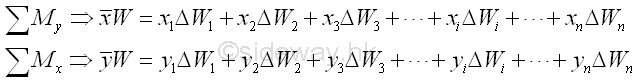
Therefore the coordinates x , y of the center of gravity of the plane plate is 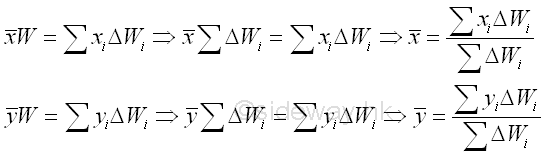
When the number of elements n is increaed toward infinity by taking the limit as the size of each element approaches zero, the magnitude of weight and the position of center of gravity of the plane plate can be determined by, 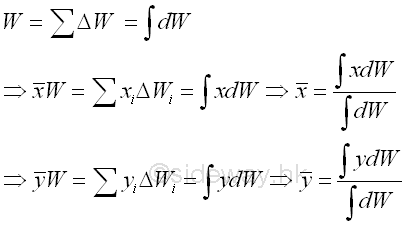
Center of Gravity of a Plane Wire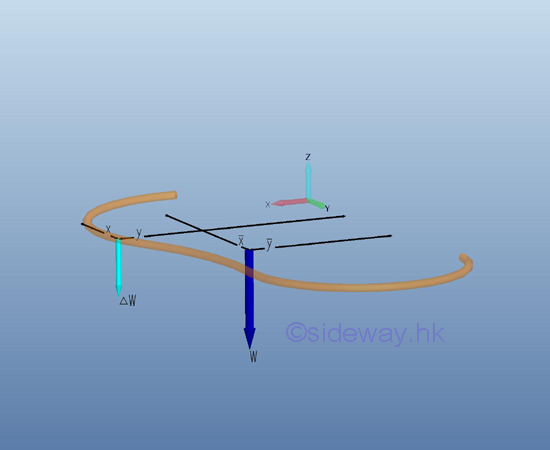
When the plane body is in the form of plane wire lying in the xy plane, the magnitude of weight and the position of center of gravity of the plane plate can be determined in the similar way. The derived equation is same as the plane plate, imply 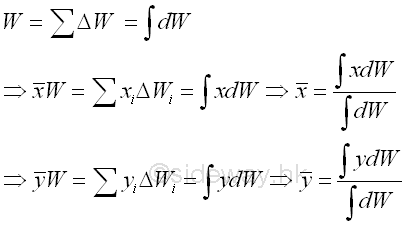
Although the center of gravity of a plate is usually located on the plate, the center of gravity of a wire is usually not located on the wire. Center of MassThe weight of an object is the gravitational force exerted by the earth on the body and can be defined as the mass of the object times the acceleration due to gravity between the object and the earth. Mass is the fundamental property of an object and is defined as the numerical measure of the amount of inertia matter of the object. Although, in general, the gravitational force field of earth is not uniform. For example, the gravitational force on an artificial satellite is not uniform. But for practical static mechanical problems, the gravitational force of earth acting on an object is usually assumed to be uniform at all places. For an uniform gravitational force field, 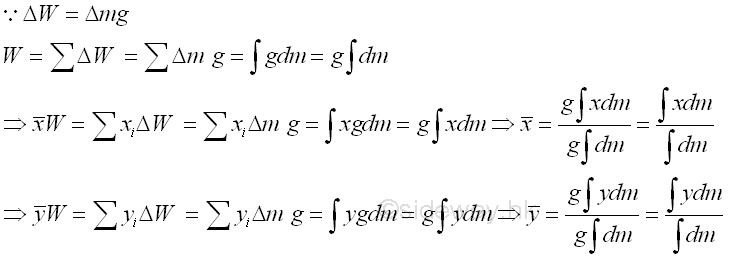
Therefore, the center of mass is same as the center of gravity in an uniform gravitational force field. Centroid of AreaThe weight of an object can also be expressed in terms of density, ρ. For a homogenous two dimensional body, plate of uniform thickness, t, the weight of an element of the plane body of area, ΔA can be expressed as, 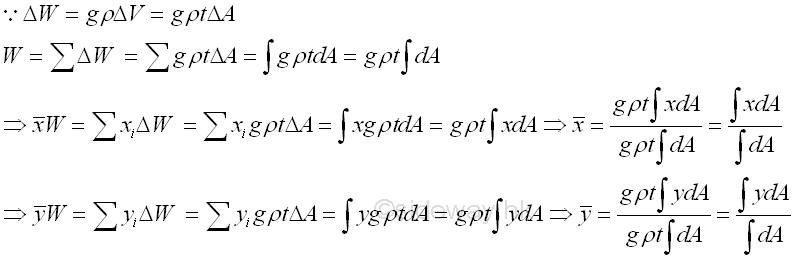
Therefore, the centroid of area of a homogeneous two dimensional body, plate of uniform thickness in an uniform gravitational force field is same as the center of gravity or center of mass. Centroid of LineSimilarly, for a homogenous two dimensional body, wire of uniform cross-section, a, the weight of an element of the wire of length, ΔL can be expressed as, 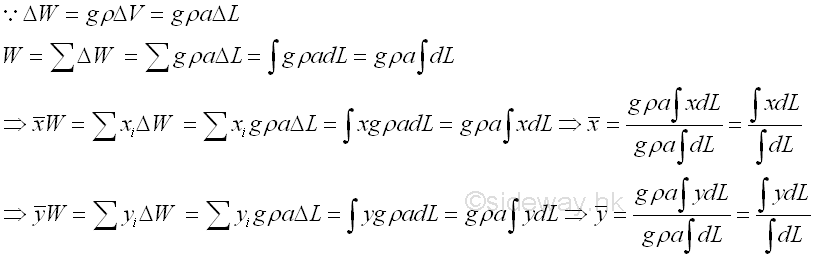
Therefore, the centroid of line of a homogeneous two dimensional body, wire of uniform cross-section in an uniform gravitational force field is same as the center of gravity or center of mass. |
Sideway BICK Blog 04/04 |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
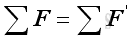 and
and