 Sideway
BICK BLOG from Sideway
Sideway
BICK BLOG from Sideway
|
Link:http://output.to/sideway/default.asp?qno=120400009 Prime Number Prime NumberPrime NumberPrime numbers are natural numbers, e.g. 2, 3, 5, 7,..., which can only be divided by 1 and itself. For other natural numbers, neither 1 nor prime number, they are called composite numbers. In general, a composite number can be expressed as a product of two factors, i.e. n=xy. 1 is not a prime because 1 can only be divided by 1 and 1 has one divisor, 1 only. Besides, prime numbers are always positive numbers. And 1 and 0 is neither prime nor composite. There are infinitely prime numbers. 2 is one of most oddest prime number. 2 is the only even prime number because any even number greater than 2 is divisible by 2. 2 is also the smallest prime number. Similarly, 5 is the only prime number ends in 5 because any number end in 5 is divisible by 5. There is no prime number ends in 0 because any number ends in 0 is divisible by 2 and 5. Therefore, except 2 and 5, all prime numbers end in 1, 3,7, or 9. And all prime numbers above 3 can be expressed in the form 6n-1 or 6n+1. FactorizationAny non-zero natural number, n can be factored into primes and expressed as a product of primes and powers of primes, n=xy=apbqcr. where n, x, y, p,. q, and r are natural numbers, and a, b, and c are prime numbers. The powers p, q, and r must greater or equal to one. Since all facors of an integer are primes, the factorization is call prime factorization. The prime factorization of an integer is unique except for the ordering of the factors. PrimalitySince a prime number, p can only be divided by 1 and itself, one of the method to verify the primality of a integer number, p is by trial division. For a composite number, the integer number n can be factored into two numbers, one of the possible factor is therefore must be less or equal to the square root of n, √n. And for an integer n greater than 1, there is always a prime number p such that n<p<2n. DivisibilityThe divisibility of an integer number for some integers can be examined by some rules:
Last DigitThe last n digits of the product of integers is equal to the last n digits of the product of last n digits of the integers. And the last digit of the n power of an integer is equal to the n power of the last digit. CyclisityThe cyclisity of the last digit in the integer power, greater than 0, of an integer with the last digit:
Greatest Common Divisior (GCD)The greatest common divisor (gcd), or greatest common factor (gcf), or highest common factor (hcf) of a set of two or more non-zero integers is the largest positive integer that can divide the set of integers without a remainder. In order to find the common factor, the prime factorization should be used for determining the factors of all numbers. The greatest common factor of the set of numbers can be obtained by multiplying the greatest common factors of all prime factors of the set of numbers, i.e. multiply the lowest power of common prime factors. imply 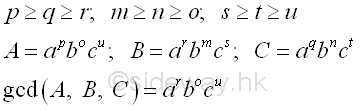
Therefore every common factor of the set of numbers is a divisor of the greatest common divisor, gcd, of the set of numebrs. Euclidean algorithmEuclidean algorithm or Euclid's algorithm is an effective technique to determine the greatest common factor GCD of two numbers through iteration. The Euclidean algorithm makes use of the greatest common factor proporty of two numbers by assuming the two numbers as the multiples of the two numbers and then reducing the multiple factors through iteration. Imply 
The iterative steps of Euclidean algorithm or Euclid's algorithm can be expressed as a recursive equation, imply 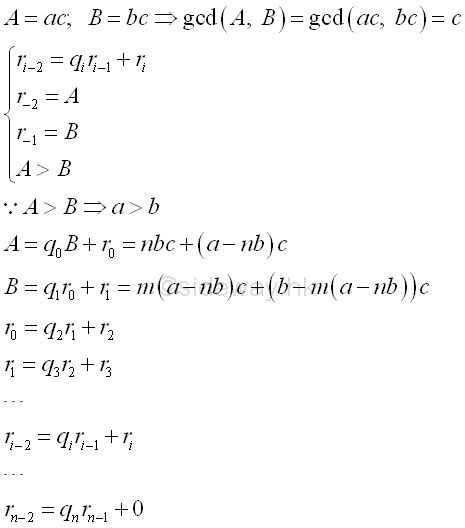
Bezout's IdentityBy reversing the Euclidean algorithm or Euclid's algorithm, the greatest common factor GCD of two numbers can be expressed the sume of two numbers which are obtained by multiplying a positive and a negative integers to the original numbers respectively in the form of ax+by=d where x and y are integers of Bezout coefficients of integers a and b and integer d is the common divisor of integers a and b. Imply 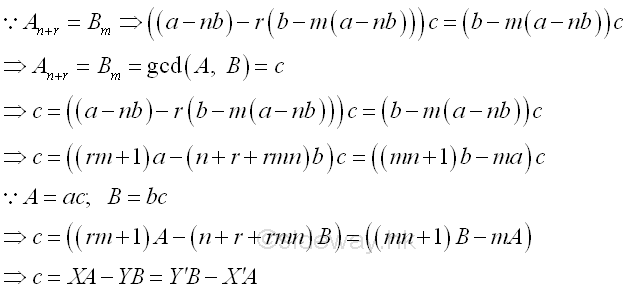
Least Common Multiple (LCM)The least common multiple (lcm), or lowest common multiple (lcm), or smallest common multiple (scm) of a set of two or more non-zero integers is the least positive integer that can be divided by the set of integers without a remainder. In order to find the common multiple, the prime factorization should be used for determining the factors of all numbers. The least common multiple of the set of numbers can be obtained by multiplying the least common multiples of all prime factors of the set of numbers, i.e. multiply the highest power of common prime factors. imply 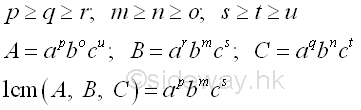
If one of the number is equal to 0, then the least common multiple, lcm, is defined as zero. Besides, the product of two numbers can be expressed the product of least common multiple and greatest common divisior of the two numbers. Imply 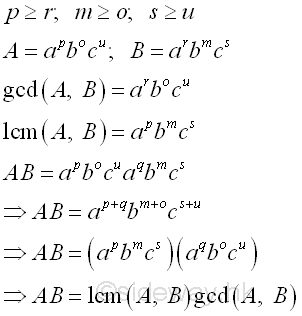
Modular ArithmeticModular arithmetic is also call clock arithmetic because modular arithmetic is a arithmetic for integers with number line wrap around like a clock, where number counting from 0 to a number m-1 for modulus m cyclically . e.g. number line of modulus 12 is 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 0, 1, 2,... Let q be the quotient and r be the remainde when a number x is divided by modulus m. Imply 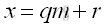
The remainder can be represented by 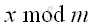
Let p be the quotient and r be the remainder when a number y is divided by modulus m. Imply 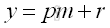
The remainder can be represented by 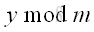
For m≥2, both x and y have the same remainder when divided by m, the relationship between x and y can be expressed as 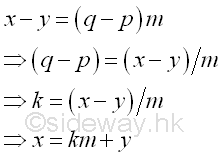
Since q, and p are integers, k is integer also. In other words, m divides (x-y) 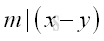
Therefore both x and y are equivalent modulo m, x and y are said to be congruent modulo m, or x is congruent to y modulo m. Imply 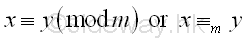
|
Sideway BICK Blog 14/04 |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||

