Summation of Accumulative Physical Quantity

The application of integration can also be applied to other mechanical quantities by expressing the mechanical quantity in the form of accumulative mechanical quantity.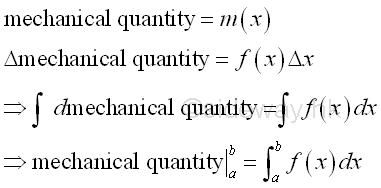

Moment of Inertia

Moment of inertia is a measure of the resistance of an object body to change its rotational motion about an axis of rotation. For an object particle, the moment of inertia can be defined as the product of particle mass m of the object particle and the square of the radius of rotation about a reference point.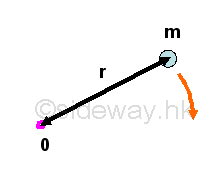

Moment of inertia of a particle of mass m about a reference point 0 with radius of rotation r is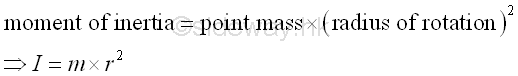

Moment of inertia of an uniform narrow bar rotating about one of the end of bar

For an uniform narrow bar of mass m, the moment of inertia of the bar rotating about its end can be obtained by slicing the moment into infinitesimal moment elements caused by infinitesimal mass elements.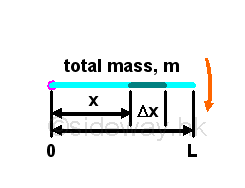 

Since the bar is uniform, the infinitesimal mass element can be expressed as mass per unit length, imply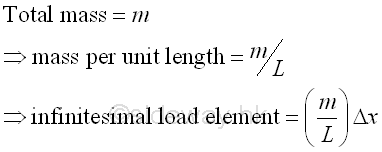

Moment of inertia of an uniform narrow bar rotating about its end is.

Moment of inertia of an uniform narrow bar rotating about the midpoint of bar

For an uniform narrow bar of mass m, the moment of inertia of the bar rotating about its midpoint can be obtained by slicing the moment into infinitesimal moment elements caused by infinitesimal mass elements.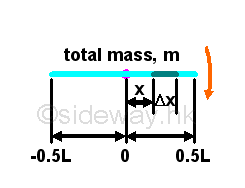 

Since the bar is uniform, the infinitesimal mass element can be expressed as mass per unit length, imply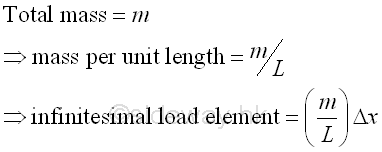

Moment of inertia of an uniform narrow bar rotating about its end is.

Moment of inertia of an uniform rectangular plate about its edge

For an uniform rectangular plane of mass m, the moment of inertia of the rectangular plate rotating about its edge can be obtained by slicing the moment into infinitesimal moment elements caused by infinitesimal mass strip elements parallel to the rotating axis.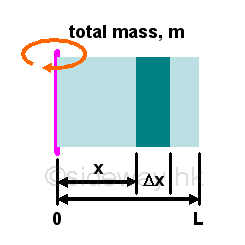 

Since the rectangular plane is uniform, the infinitesimal mass element can be expressed as mass per unit length, imply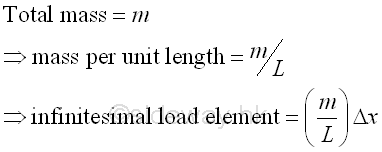

Moment of inertia of an uniform rectangular plane rotating about its edge is.

Moment of inertia of an uniform rectangular plate about its bisector

For an uniform rectangular plane of mass m, the moment of inertia of the rectangular plate rotating about its bisector can be obtained by slicing the moment into infinitesimal moment elements caused by infinitesimal mass strip elements parallel to the rotating axis.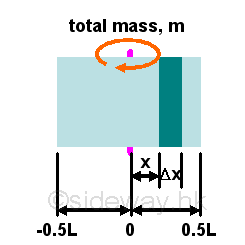 

Since the rectangular plane is uniform, the infinitesimal mass element can be expressed as mass per unit length, imply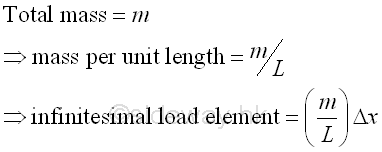

Moment of inertia of an uniform rectangular plane rotating about its bisector is.

Moment of inertia of a circular plate about its diameter

For a circular plate of mass m, the moment of inertia of the circular plate rotating about its diameter can be obtained by slicing the moment into infinitesimal moment elements caused by infinitesimal mass strip elements parallel to the rotating axis. 

Since the circular plate is uniform, the infinitesimal mass element can be expressed as mass per unit area, imply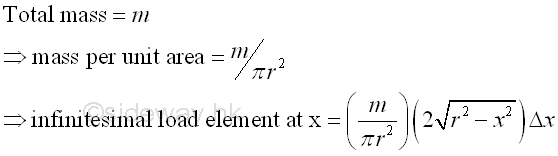

Moment of inertia of a circular plate rotating about its diameter is.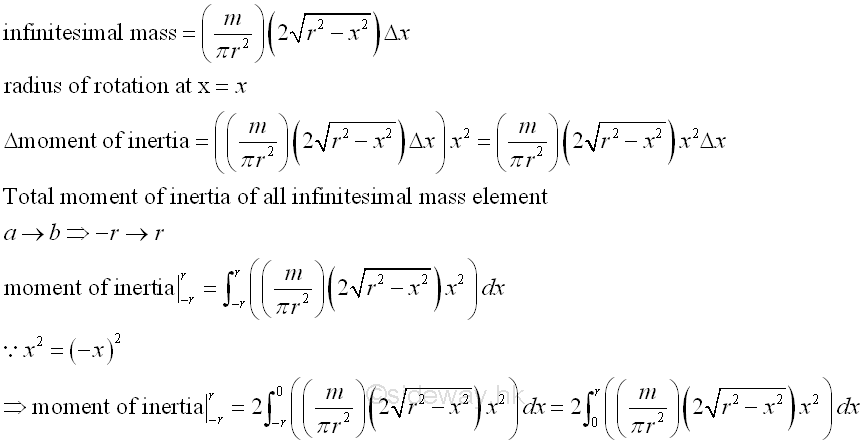

Through substitution