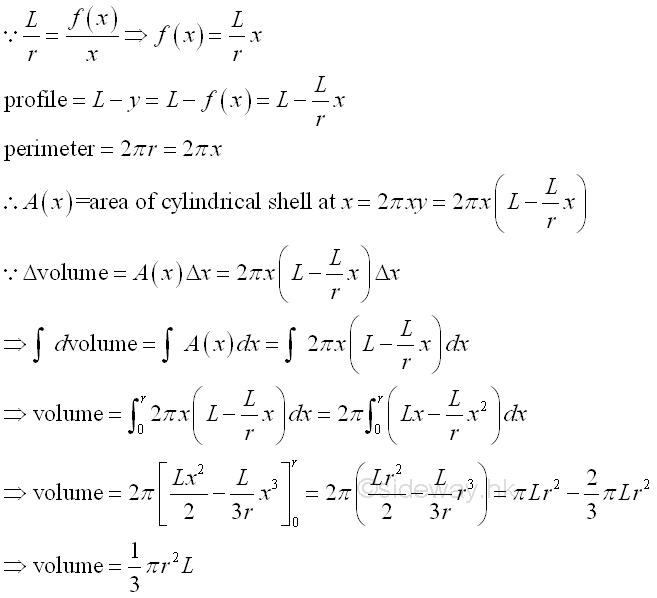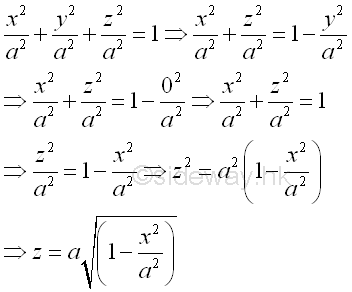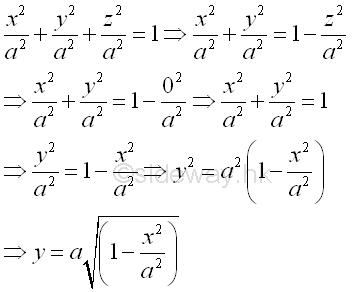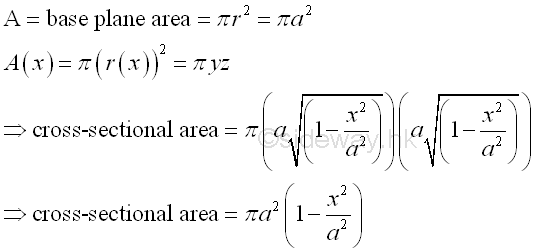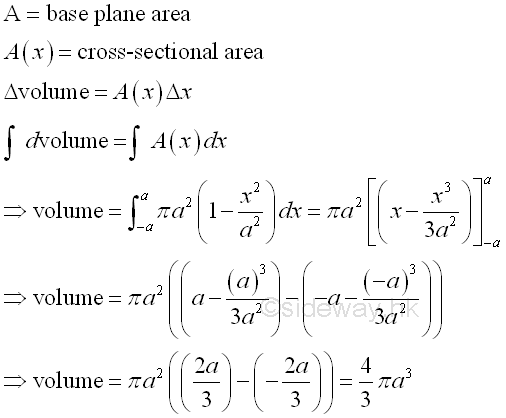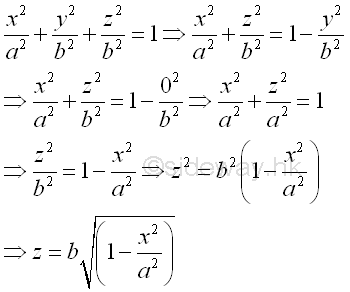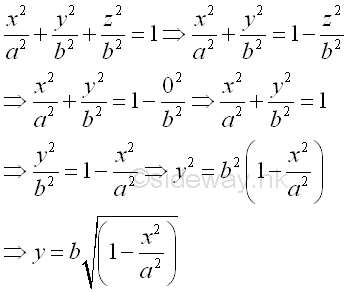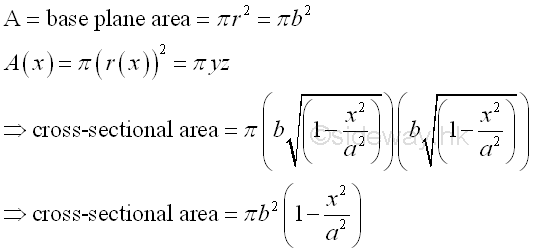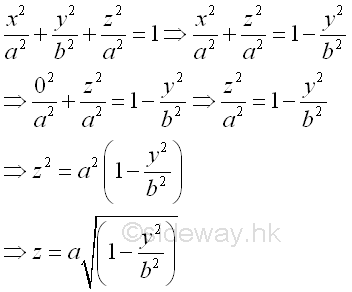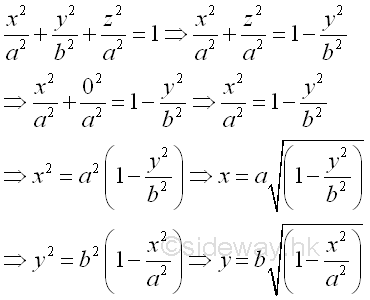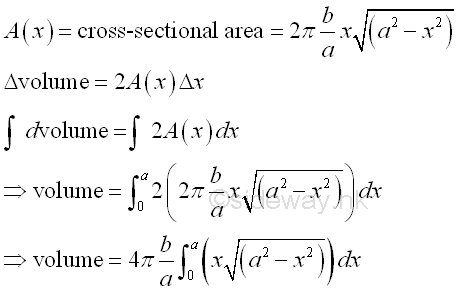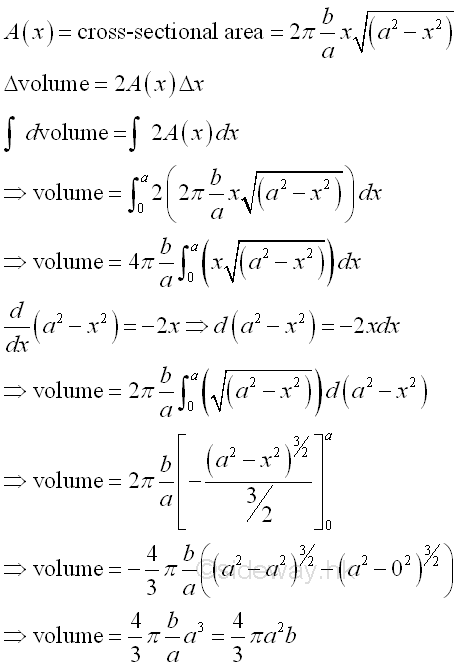Sideway
BICK BLOG from Sideway
Sideway
BICK BLOG from Sideway
|
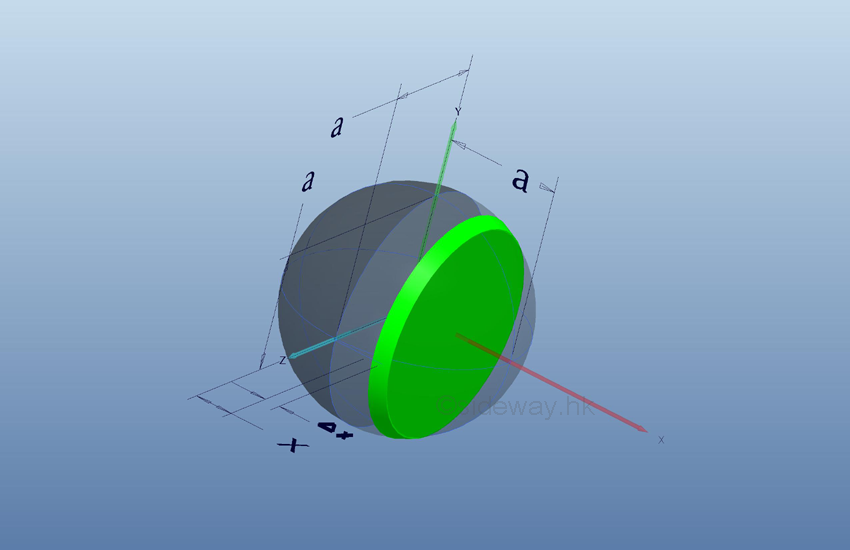
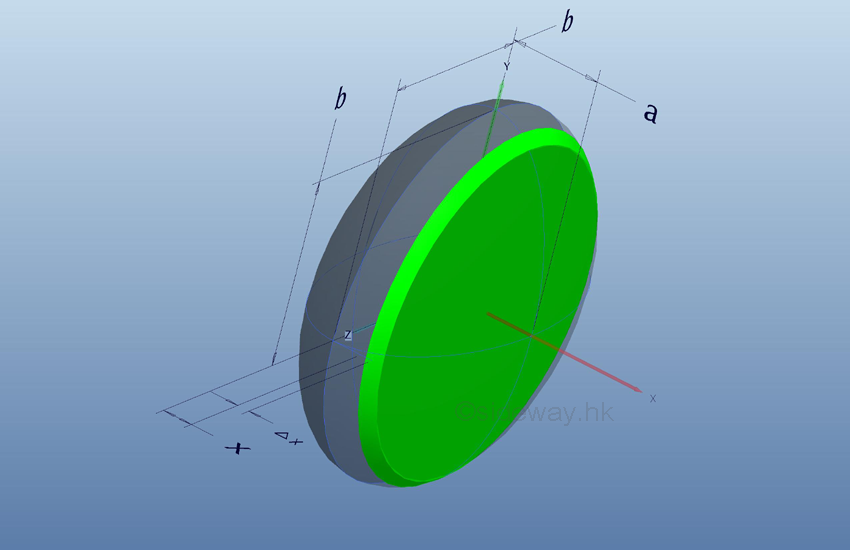
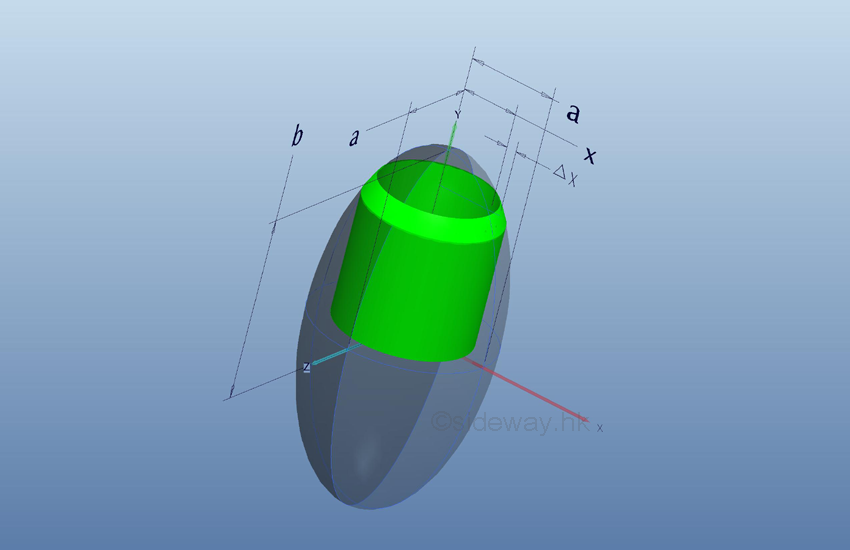
Link:http://output.to/sideway/default.asp?qno=111200002 Volume of Common Solids Summation of Accumulative Physical QuantityBesides the extrusion of a filled area profile, volumes of some common solids can also be obtained by expressing an infinitesimal volume element as the revolution of a profile. There are two types of volumes of revolutions used in the calculation of the volumes of some common solids formed by revolution. The difference between the two types of volumes of revolutions is the axis of relvolution relative to the summation direction of the infinitesimal volume elements. The disc method is the axis of revolution is parallel to the summation direction. This method is simular to the extrusion of filled profile but the filled profile should be defined in the form of πr2 . It is called disc method because the infinitesimal volume elements is in the form of a disc. 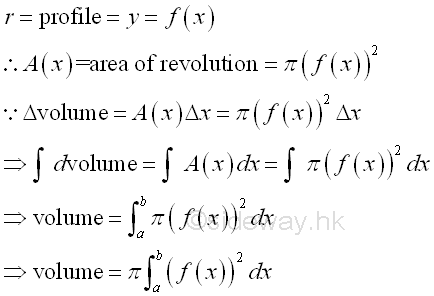
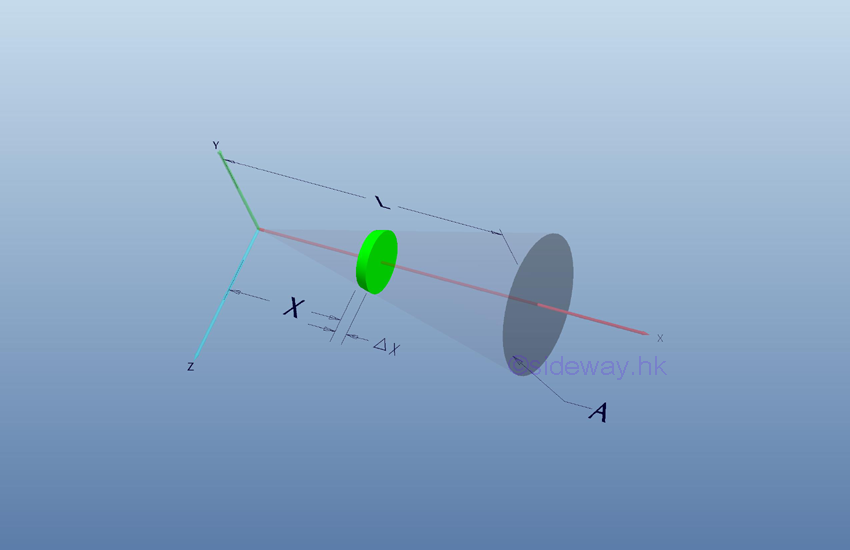
The shell method is the axis of revolution is normal to the summation direction or the infinitesimal volume element is summed radially. It is called cylinder method because the infinitesimal volume elements is in the form of a cylindrical shell. 
Volumes of Common Solids
|
Sideway BICK Blog 04/12 |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||