 Sideway
BICK BLOG from Sideway
Sideway
BICK BLOG from Sideway
|
Link:http://output.to/sideway/default.asp?qno=111200004 Work Summation of Accumulative Physical QuantitySimilar to the extension of finding accumulative physical quantity from area to volume, the application of integration can be used to calculate some variable mechanical quantity by expressing the mechanical quantity in the form of accumulative mechanical quantity. 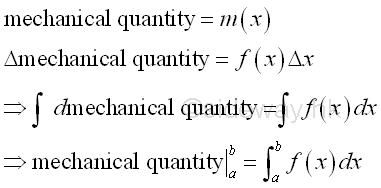
Work by a ForceWork can be defined as the product of a force acting upon an object and the displacement of the object caused by the applied force. 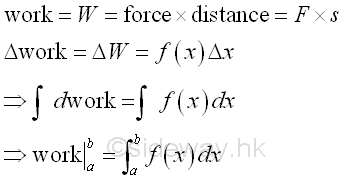
For a constant force F, imply 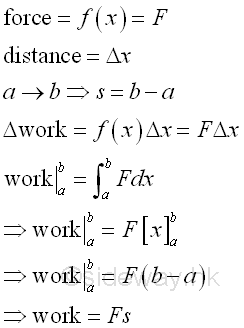
Work to compress or stretch a springFor a variable force f(x) such as spring force, the force varies with the length of spring, 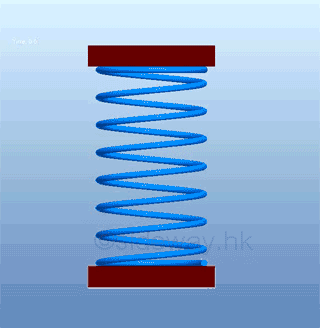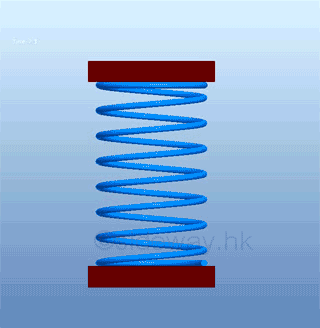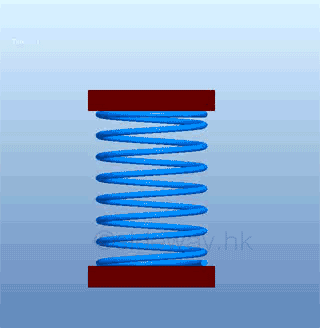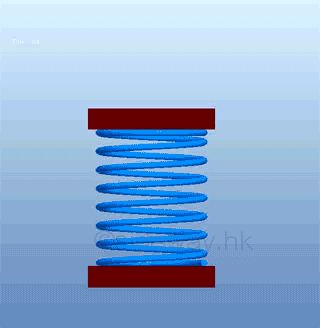
The force of a spring is proportional to the length of compression or extension from its natural length. Graphically, the work done by spring is, 
For a spring of natural length 20 with k equals to 1, the force when the length of spring is compressed to 16 is equal to 4. The distance and work done of spring compresssion is therefore equal to 
And geometrically, the work is equal to the area under the curve, that is half of the product of force and travelled distanct, (kx*x)/2. For a spring of natural length 20 with k equals to 1, the distance and work done of spring compression from 16 to 12 is equal to 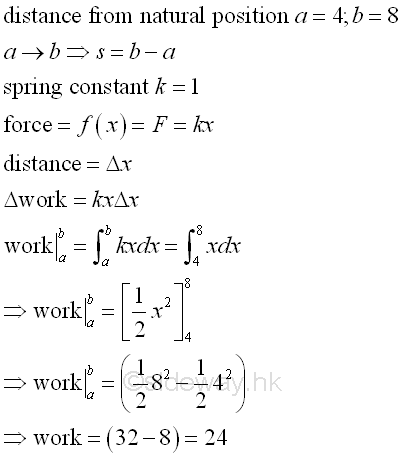
Both the applied force and the displacement always have the same direction in compressing or stretching the spring , they have the same sign. Therefore, for a spring of natural length 20 with k equals to 1, the distance and work done of spring extension from 24 to 28 is same as the work done of spring compression from 16 to 12. Work to move an objectWork done on an object is equal to the travelled distance multiplied by the applied force along the travelling direction. In general, the amount of work done by an applied force to move an object with equal displacement along the applied force in any direction is the same. 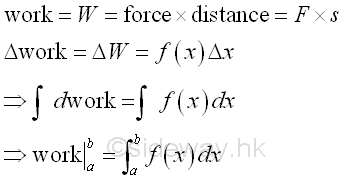
Work to lift a load with a light wireFor a light wire, the weight of the wire can be neglected. The total work done is obtained by slicing the work into infinitesimal work elements. Since the applied force to lift the load is a constant, the amount of work done is equal to the applied force times the displacement. 
Work to lift a load of 20 from ground 0 to a 30 high platform is. 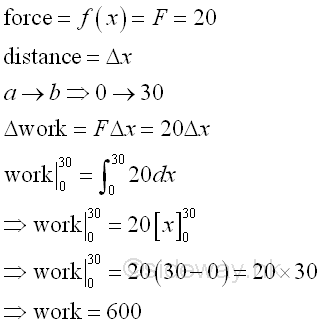
Work to lift a variable loadFor a light wire, the weight of the wire can be neglected. If the load is a leaky sandbag with leaking rate 0.1 per unit travelled length, the load becomes a variable load. The applied force to lift the load decreases with the height because of sand leaking. The total work done is obtained by slicing the work into infinitesimal work elements. The amount of work done is equal to the summation of the infinitesimal work elements. Work to lift a leaky load of 20 from ground 0 to a 30 high platform is. 
Work to lift a load with a heavy cableFor a heavy cable with 0.1 per unit length, the weight of the cable can not be neglected. The applied force to lift the load should include the weight of the lifting cable, therefore the total load is decreasing while lifting the object because the length of cable is reducing. Unlike the concentrated load, the cable load is a distributed load along the lifting direction, therefore the travelled distance for each infinitesimal load element is not the same and all infinitesimal work elements by each infinitesimal load element should be calculate individually. And the total work done is then obtained by the summation of all infinitesimal work elements by each infinitesimal load element and the concentrated load. Work to lift a load of 20 from ground to a 30 high platform is. 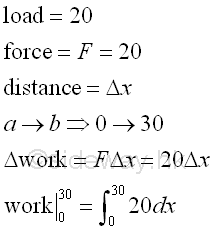
Work to lift a heavy cable with 0.1 per unit length from ground to a 30 high platform is. 
Total work to lift a load of 20 with a heavy cable with 0.1 per unit length from ground to a 30 high platform is 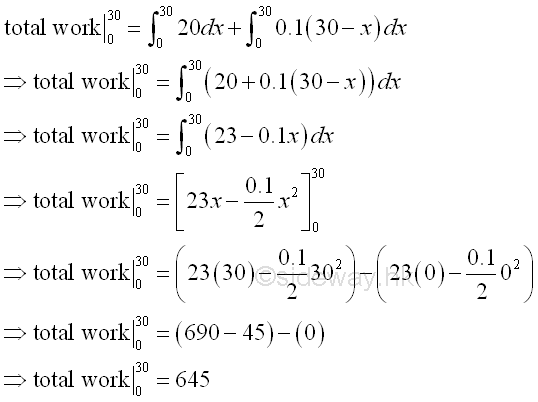
Work to raise fluidSimilar to lifting a heavy cable, raising fluid in a tank can be considered as moving fluid layer by layer, therefore problem of raising fluid from a tank to a higher level is also a problem of moving a distributed load. Work to raise fluid in a cylindrical tankFor a cylindrical tank, the cross-sectional area of the tank is equal, therefore the work done to raise fluid for every infinitesimal layer element is the same. 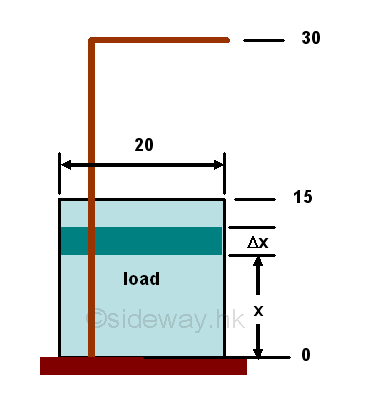
Work to raise a layer of density 1 per unit volume fluid from a cylindrical tank of diameter 20 with fluid height 15 to a level15 above the tank, that is a 30 high from the ground is. 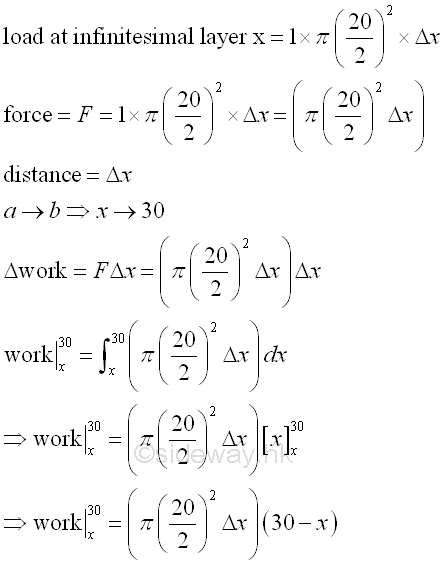
Total work to raise all fluid from 0 to15 in the tank to a level 15 above the tank is. 
Work to raise fluid in a conical tankFor a inverted conicall tank, the cross-sectional area of the tank varies with height, therefore the work done to raise fluid for every infinitesimal layer element varies with height also 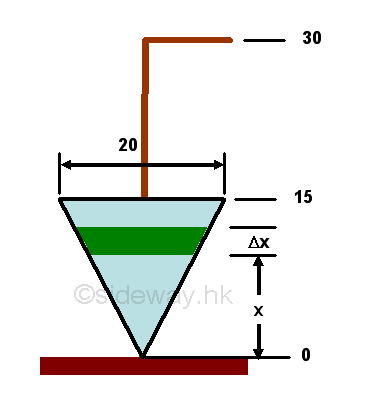
Work to raise a layer of density 1 per unit volume fluid from a conical tank of base diameter 20 with fluid height 15 to a level15 above the tank, that is a 30 high from the ground is. 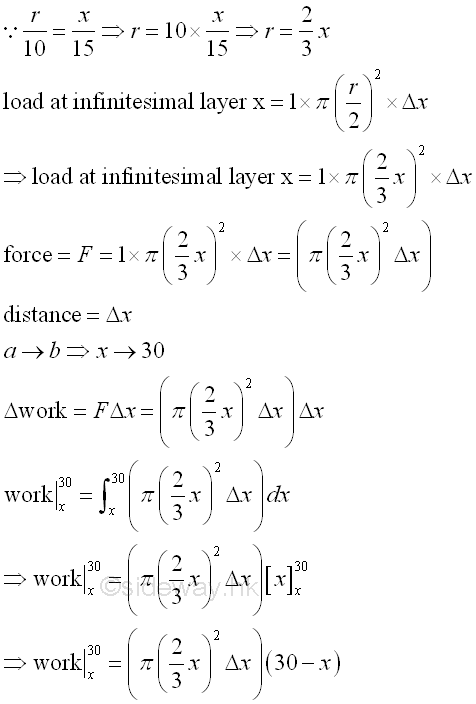
Total work to raise all fluid from 0 to15 in the tank to a level 15 above the tank is. 
|
Sideway BICK Blog 13/12 |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||

