 Sideway
BICK BLOG from Sideway
Sideway
BICK BLOG from Sideway
|
Link:http://output.to/sideway/default.asp?qno=100900019 Law of Conservation Law of Conservation
Based on linear acoustic, assuming the
cross-section area equals to A and no mass is entering or leaving the system due to the acoustic
disturbance, the wave propagation can be represented by following figure: 
where, at ambient environment and at acoustic disturbance state:
where,
properties of acoustic disturbance: 
where,
properties at wavefront: 
Continuity Equation, 1D
For a control volume, from the principle of conservation of mass, the instantaneous rate of change of
mass in a control volume equals to the net mass flux flow into or out
of the control volume, therefore: 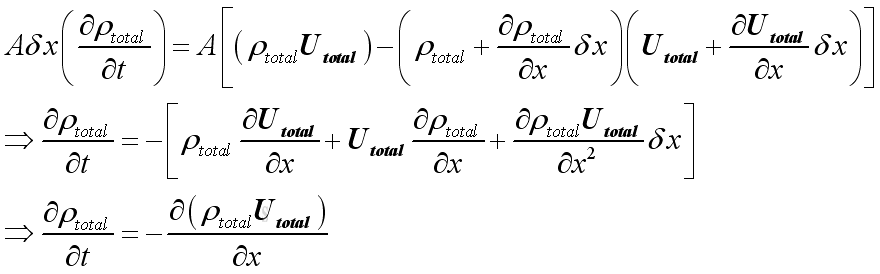
The relationship between density and velocity is defined Euler's Equation of Inviscid Motion, 1D
For a control volume, from principle of momentum conservation, the
instantaneous rate of change of net momentum of a control
volume equals to the net applied force and the net momentum change due to the
momentum flux flow into or out of the control volume. The applied force in
this case is pressure only and no other forces, no gravity, no viscous force
etc., then: 
Since both Utotal , ρtotal are a function of time, imply: 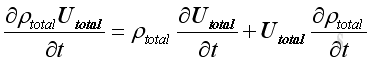
Therefore, because of conservation of mass, the equation is: 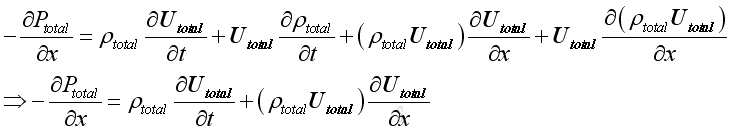
As the medium fluid is assumed to be inviscid, the assumption of inviscid flow is valid for sound propagation and the euler's equation of motion can be applied. The additional relationship between pressure and velocity is defined Energy Equation, 1D
For a control volume, from principle of energy conservation, rate of change of
energy equal to rate of heat added and the net rate of energy flow into or out
of the control volume minus the rate of work done. By neglecting heat energy
and external work, and potential energy then: 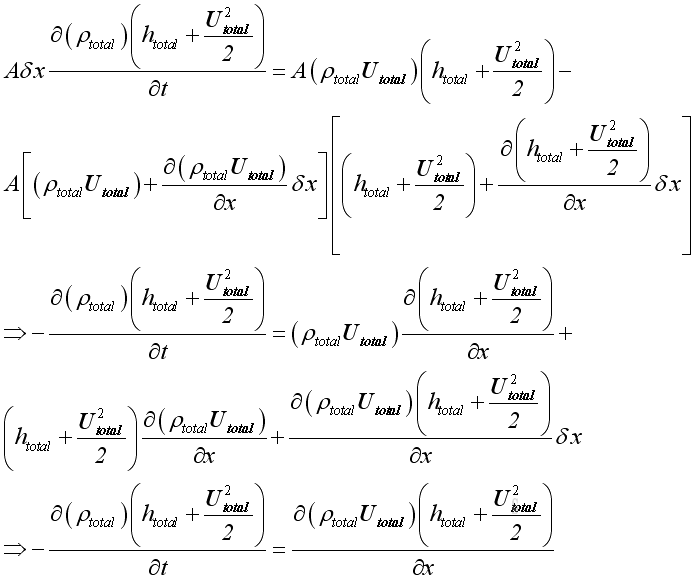
The additional relationship between Enthalpy and velocity is defined. Link:http://output.to/sideway/default.asp?qno=100900020 Acoustic Wave Propagation, 1D Acoustic Wave Propagation
Based on linear acoustic, assuming the
cross-section area equals to A and no mass is entering or leaving the system due to the acoustic
disturbance, the wave propagation can be represented by following figure: 
where, at ambient environment
and at acoustic disturbance state:
where,
properties of acoustic disturbance: 
where,
properties at wavefront: 
Acoustic Propagation Properties
Since the acoustic pressure variations is much smaller than the ambient
pressure, the total pressure approximately equals to the ambient pressure.
Similarly, the acoustic density variations is also much smaller than the
ambient medium density, the total medium density approximately equals to the
ambient medium density. For a quiescent medium, the initial medium velocity equals to
zero, therefore the total velocity equals to the acoustic velocity variations. 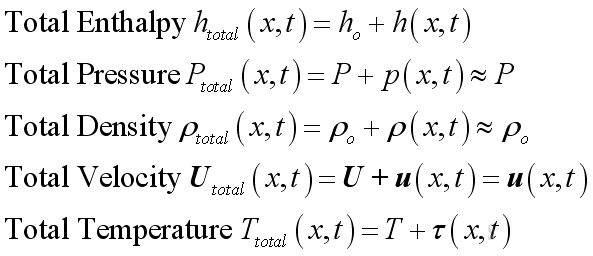
Besides, for a homogenous quiescent medium, the initial medium velocity, the
ambient pressure and the ambient medium density are constant and independent of
time and position. Therefore: 
Linearized Acoustic Wave Equation, 1D
Since both u
, ρ are very small
when comparing with ρo and they are a
function of time and position, equations can be linearized by neglecting
second and higher order terms.
Substitute.variables
approximation into continuity equation
and linearize the equation by neglecting second and higher order terms, then: 
The time derivative of the equation is 
Substitute.variable
approximations into equation
of motion and linearize the equation by neglecting second and higher order terms, then: 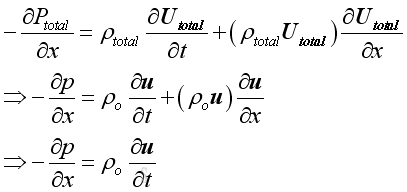
The position derivative of the equation is 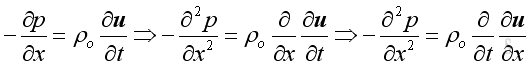
Therefore, equate the conservation of mass and conservation of momentum, then: 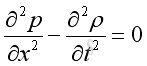
To simplify the equation, the equation of state is applied and to make the equation more practical, the equation is expressed in term of the fluctuating pressure, which can be measured easily. Then 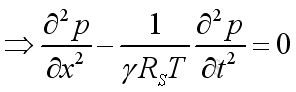
Speed of Acoustic Wave PropagationFor a control volume, when reducing the control volume to the medium at the wavefront of acoustic wave propagation, from the principle of mass conservation, the mass of medium in the control volume should be constant.
Assume c
is the speed of wavefront propagation and propagates away from the source, and Δu is the acoustic velocity
fluctuation, since the fluctuation is a relative velocity to the wave
propagation, the net medium velocity is
c-Δu at the acoustic source side. Then 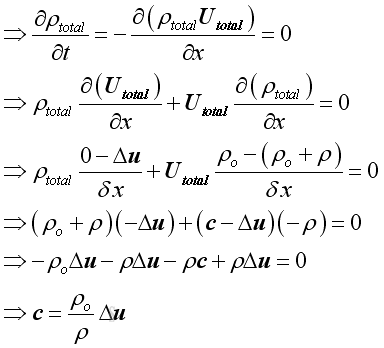
Alternately, the continuity equation can be expressed as the
net instantaneous mass flow into and out of the control volume to be equal. Then 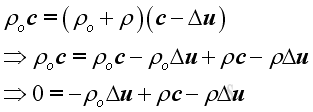
Since c is much greater than Δu, therefore: 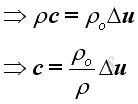
Similarly, for the same control volume, from principle of energy conservation, the energy of medium in the control volume should be constant.
Assume Δh
is the acoustic enthalpy variations of the medium in the control volume. Since
ρtotalutotal
is not equal to zero and conservation of mass, by neglecting second
order small term. Then: 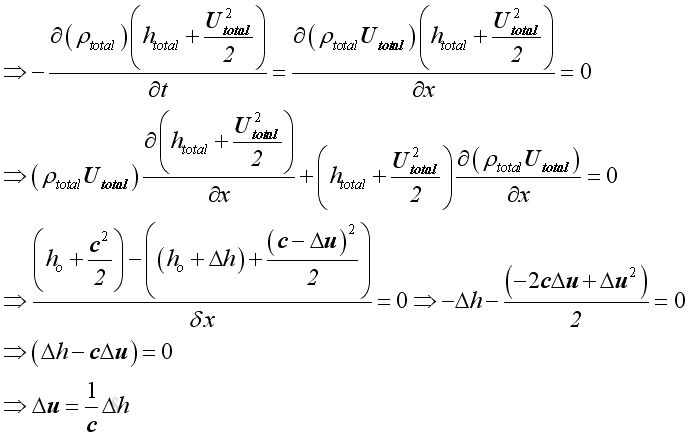
Alternately, the conservation of energy can be expressed as the net instantaneous energy flow into and out of the control volume to be equal. Then 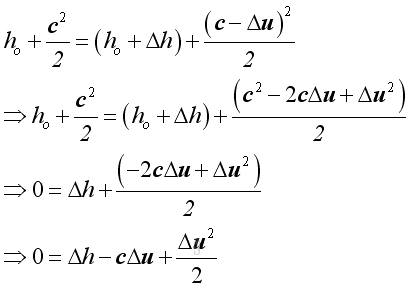
Neglecting second order small term. Then 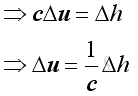
Equating mass conservation and energy conservation. Then 
The acoustic disturbance is small and can be assumed as an isentropic process. Imply 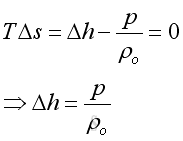
Substitute Δh into the equation of wave propagation, Imply 
Since both ρ and p are the small acoustic fluctuation, and under isentropic process, imply 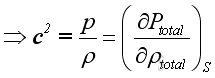
For an isentropic process, imply 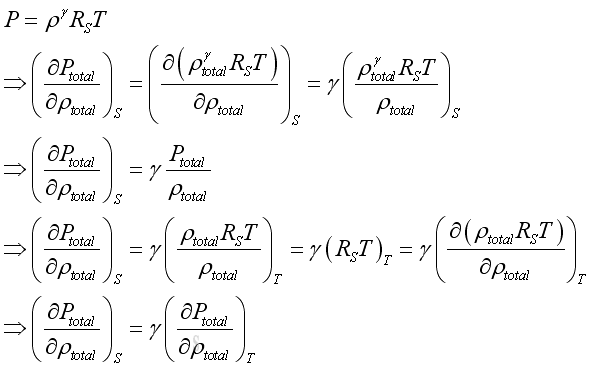
Substitute into the equation of wave propagation, Imply 
Wave Equation, 1DSubstitute the speed of wave propagation into the wave equation, Imply 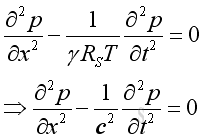
|
Sideway BICK Blog 13/09 |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
 and,
and,


