 Sideway
BICK BLOG from Sideway
Sideway
BICK BLOG from Sideway
|
Link:http://output.to/sideway/default.asp?qno=100900021 Acoustic Plane Wave Acoustic Plane WaveFor a 1D acoustic plane wave in x direction,: 
where
p is a function of
x and t.
The general solution of the equation is an arbitrary wave propagation along positive x direction and negative x direction. 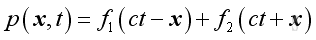
For ct-x, the propagation of pressure fluctuation should be repeated after the period ct-x, therefore after time t, the wave should propagate a distance x in positive direction outwardly. But for ct+x, the propagation of pressure fluctuation should be repeated after the period ct+x, therefore after time t, the wave should propagate a distance x in negative direction inwardly. Since p is a function of x and t, it is characteristic by a double periodicity. In time domain 
where
ω is angular velocity And in physical domain: 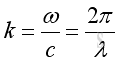
where
k is wave number Consider a solution of the form: 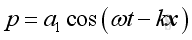
where
ω is the angular frequency
and

Substituting into the 1D wave equation and the form of solution is confirmed.

Therefore the general harmonic wave solution of wave equation is: 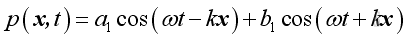
Similarly, consider a solution of the form: 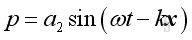
where
ω is the angular frequency
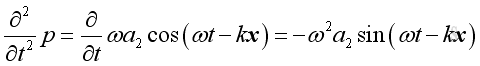
and

Substituting into the 1D wave equation and the form of solution is confirmed also. Since the 1D wave equation is linearized by making the differential coefficient is of first order only, the sum of two solution forms is also a solution of the wave equation. The differences between two solutions are the phase angle and the magnitude. 
The general expression of a harmonic function is: 
and it can be decomposed into sinusoidal and cosinusoidal components in quadrature of 90 degrees out of phase: 
These two components can be individual harmonic function with arbitrary phase angle φ as in the first two solutions. Or they can be linked solution in a linear system in which the phase angle is not an arbitrary and is related as in the above solution: Complex Exponential RepresentationSince in complex system, 
The solution of wave equation can be expressed in a complex exponential form, 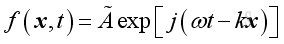
where
à is Complex function of the form
a+jb
Since it is a complex function, the real
acoustic pressure function can be represented by the real
part of the complex expression. 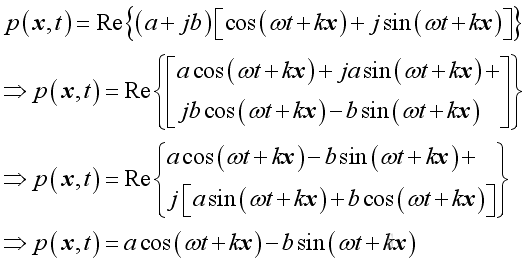
By comparing with the wave equation solution, imply: 
Therefore, the general complex harmonic wave solution of 1D wave equation is : 
Plane Wave PropertiesConsider a plane wave propagates along positive x direction:
From the linearized conservation of momentum, the relationship between acoustic pressure and acoustic velocity is: 
Therefore: 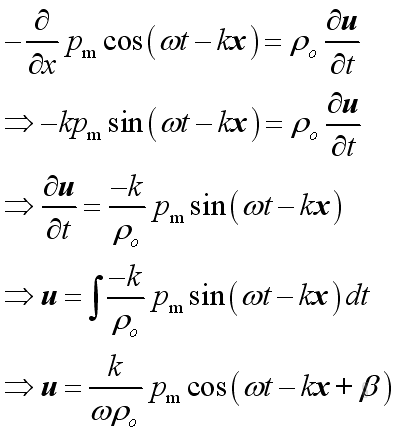
The differences in magnitude between
acoustic pressure and acoustic velocity are the relative
magnitude and the relative phase angle.
Imply : 
Therefore the relationship between acoustic pressure and acoustic velocity is: 
In general: 
Medium Acoustic ImpedanceThe acoustic impedance of a medium is defined as the ratio of acoustic pressure to the acoustic velocity, Then 
For air, z=400 Plane Wave SuperimpositionConsider two harmonic plane waves propagate of the same frequency along positive x direction and negative x direction respectively. The pressure fluctuation of two harmonic plane waves i.e. A along positive x direction and B along negative x direction are 
If the two harmonic plane waves are in phase at x=0, then the phase angle at x is equal to zero also. Therefore the pressure fluctuation of two harmonic plane waves at x are 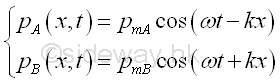
The total sound pressure at x is 
According to the linearized equation of motion, 
Imply, 
From the linearized equation of motion, imply 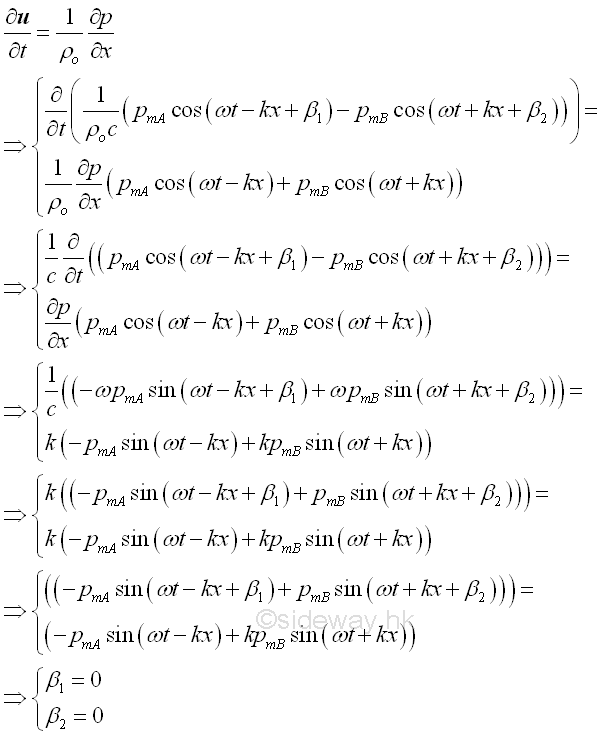
Therefore, the vector sum of the particle velocity at x is 
Link:http://output.to/sideway/default.asp?qno=100900022 URL Escape Code URL Escape CodesReference: https://graphemica.com/ last updated 7Jan2019 URL Escape Codes of Control CharactersURL Escape Codes of Control Characters
URL Escape Codes of Printed Characters
|
Sideway BICK Blog 20/09 |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
 ,
, 
 ,
,
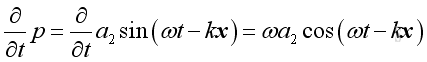 ,
,
 ,
,
 or
or

 or
or


