 Sideway
BICK BLOG from Sideway
Sideway
BICK BLOG from Sideway
|
Link:http://output.to/sideway/default.asp?qno=100900012 Trigonometry TrigonometryThe Trigonometric Functions
The Values of Common Angles of Trigonometric Functions
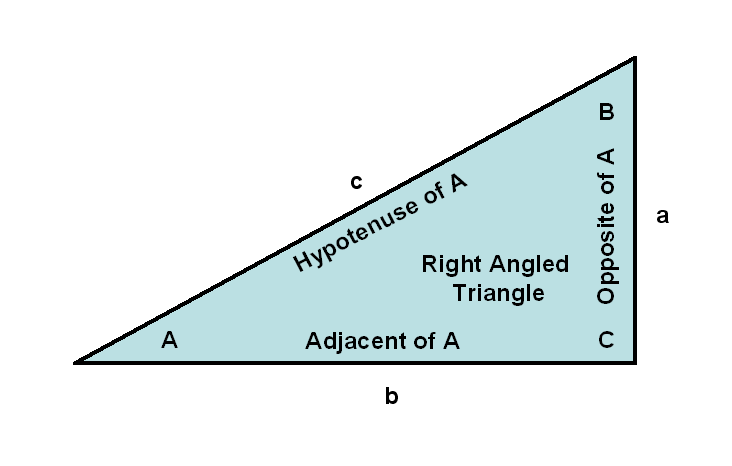
The Laws of Trigonometric Functions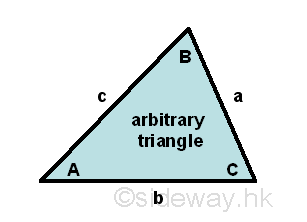
The Law of Sines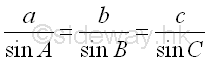
The Law of Cosines
The Trigonometric IdentitiesThe Identities of Negative Angle
The Identities of CoFunction
The Identities of Periodicity
The Reduction Formulas of Trigonometric Functions
The Identities of Angle Sum and Difference
The Pythagorean identity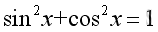
The Identities of Double Angle
The Identities of Half Angle
The Product of Cosine and Sine
Link:http://output.to/sideway/default.asp?qno=100900017 Sound Propagation Acoustic PropagationConsider a longitudinal sound wave traveling along a direction in a fluid, the acoustic disturbance propagation causes medium particle displacement in form of oscillation, and the medium particles return to its former state after the disturbance has passed. The fluid in most common engineering acoustic system can be assumed as an idea gas, and obey the perfect gas law. That is
where
P is pressure In equilibrium state, the perfect gas equation is still valid under the sound propagation process. To simplify the problem, the fluid medium is assumed to be homogeneous and isotropic that properties of the medium are same everywhere. The medium is also assumed to be perfect elastic for the sound wave propagation with no energy loss. The fluid is also assumed as an inviscid fluid with no drag force. As the fluid medium is in equilibrium, the gravitational effects on sound propagation can also be neglected. Since the acoustic oscillations are very small, the temperature gradients due to the oscillation is very small also. Nearly no heat can be transferred to other medium particle during the sound propagation process. Therefore the wave propagation process can be assumed to be adiabatic and reversible, an isentropic process. For adiabatic process, the relation of pressure and density is:
where
P is pressure The relationship of pressure and density due to sound wave is non-linear, but this non-linearity effect is usually negligible when comparing with the sound perception of ear. When the fluctuations of medium particle are small, e.g. less than 100dB, the acoustic properties can be assumed linear. Acoustic Fluctuation
At initial equilibrium ambient state, the medium is assumed to be homogeneous
and quiescent. The physical properties are independent of position and time. The
initial medium velocity also equals to zero (

At the acoustic static, assuming there is no mass entering or leaving the system for the sound propagation, the acoustic disturbance will alter the physical properties of medium and can be defined as: 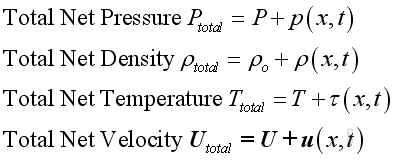
where
The acoustic fluctuation is a function of traveling distance and time. The fluid returns to its former equilibrium state after the disturbance has passed. Besides, the representation of corresponding volume or specific volume of medium are: 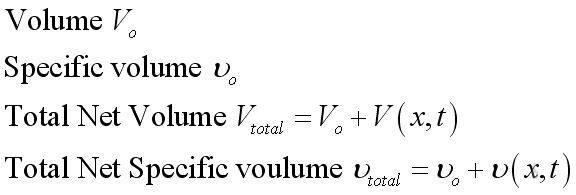
where
Vo is the initial volume of medium |
Sideway BICK Blog 09/09 |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
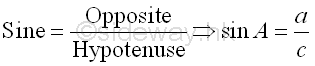

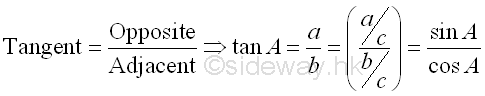
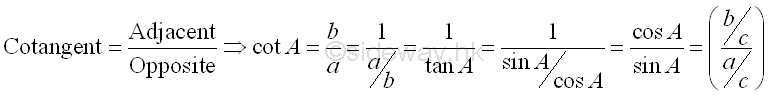
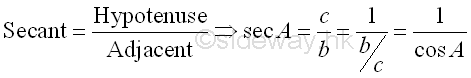
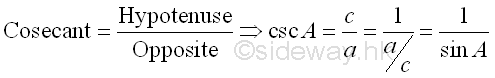
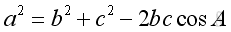
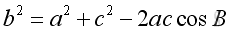
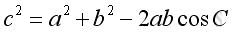
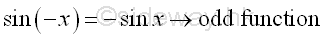
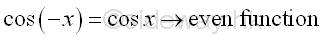
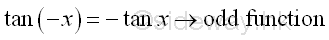
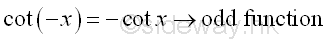
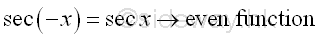
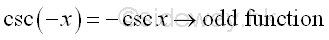
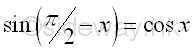
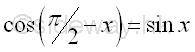
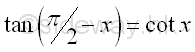
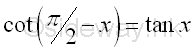
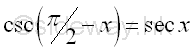
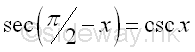
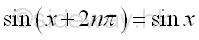
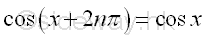
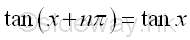
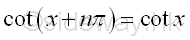
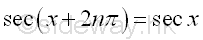
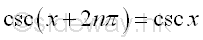
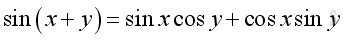
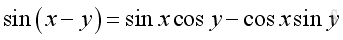
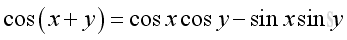
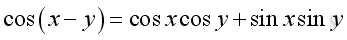
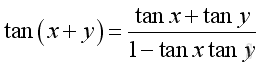
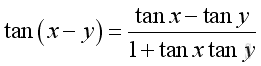
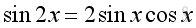
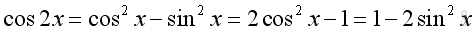
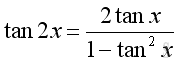
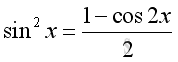
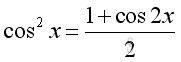
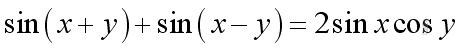
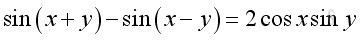
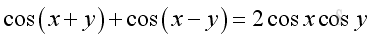
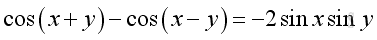
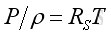 or
or
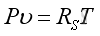 or
or
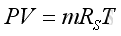 or
or
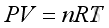 or
or
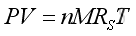
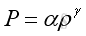 or
or
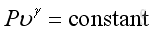
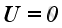 ) and the physical properties are
defined as:
) and the physical properties are
defined as: 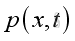 is the acoustic pressure variations
is the acoustic pressure variations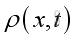 is the acoustic density variations
is the acoustic density variations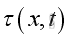 is the acoustic temperature variations
is the acoustic temperature variations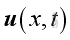 is the acoustic velocity variations
is the acoustic velocity variations
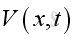 is the acoustic volumetric variations
is the acoustic volumetric variations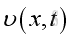 is the acoustic specific volume variations
is the acoustic specific volume variations

