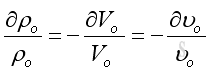Sideway
BICK BLOG from Sideway
Sideway
BICK BLOG from Sideway
|
Link:http://output.to/sideway/default.asp?qno=100900018 Equation of State Thermodynamic Equation of State
Since sound fluctuation can be treated as an adiabatic process, the
pressure is a function of density fluctuation only. That is
It can be expressed by Taylor series expansion as following 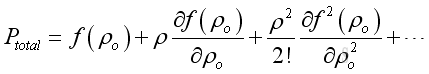
Since the acoustic fluctuation is small, the density variation is small also. The ρ2 and higher power terms can be neglected for acoustic fluctuation with moderate sound pressure. Implies: 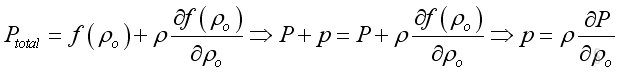
The relation of acoustic pressure variation and acoustic density variation becomes linear. Similarly, as sound fluctuation is assumed an adiabatic process, the fractional change of pressure per displacement change in term of density and specific volume generally can be expressed as
or 
For a fixed of mass, the fractional change of density and specific volume per volume change are 
or 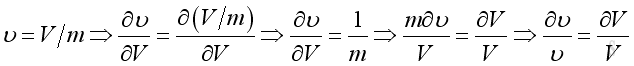
As the equilibrium pressure is much greater than the acoustic pressure, the acoustic variation of density, volume or specific volume only cause a very small acoustic pressure variation in the equilibrium pressure. Therefore, taking the fractional change at the equilibrium state is accurate enough to relate the acoustic pressure and the acoustic variation of density, volume or specific volume. And can be expressed as:
where P is pressure of medium at initial state Sub into the Tayor expansion and together with the ideal gas law, then the relationship between acoustic pressure and acoustic density variations are : 
where
p is acoustic pressure variation Therefore the relationship can be a function of absolute temperature of the medium. Considering a fixed mass with a small changes in volume and density, then: 
where
ρo is initial density of medium By neglecting the product of small quantities, then: 
Therefore, by rearrangement, the acoustic pressure can also be expressed as a function of volumetric strain: 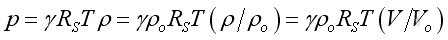
where
V is acoustic volumetric variation |
Sideway BICK Blog 11/09 |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
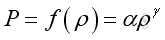 or
or

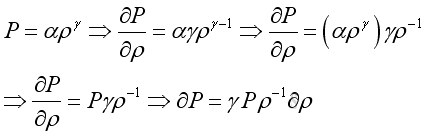
 ,
,
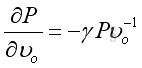 and
and