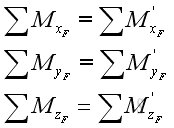Sideway
BICK BLOG from Sideway
Sideway
BICK BLOG from Sideway
|
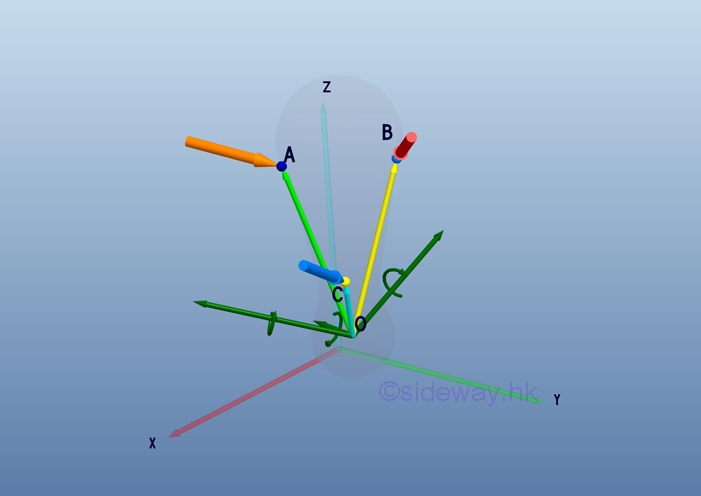
Link:http://output.to/sideway/default.asp?qno=110700013 System of Forces System of ForcesIn practical applications, there may be more than one force acting on a rigid body or the interested point subjects to the impact of forces acting on the rigid body may be changed. The system of forces may therefore need to be transformed to an equivalent system.
The impact of a system of forces acting at a point O on a rigid body can be determined by the vector sum of the forces of the system at point O and the sum of the moment of the forces of the system about the point O.
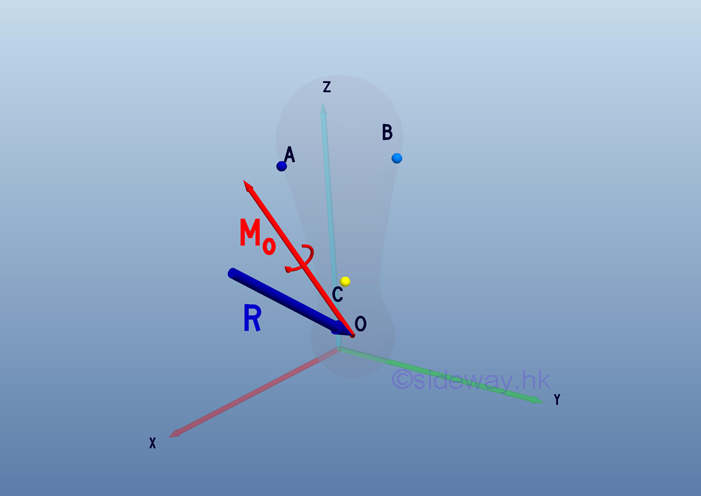
Therefore, the equivalent system should includes a force vector R to provide the resultant linear motion and a couple vector MO to provide the resultant rotational motion as the system of forces at point O. When the resultant force vector R is equal to zero, the equivalent system can be reduced to a single couple vector MO system.
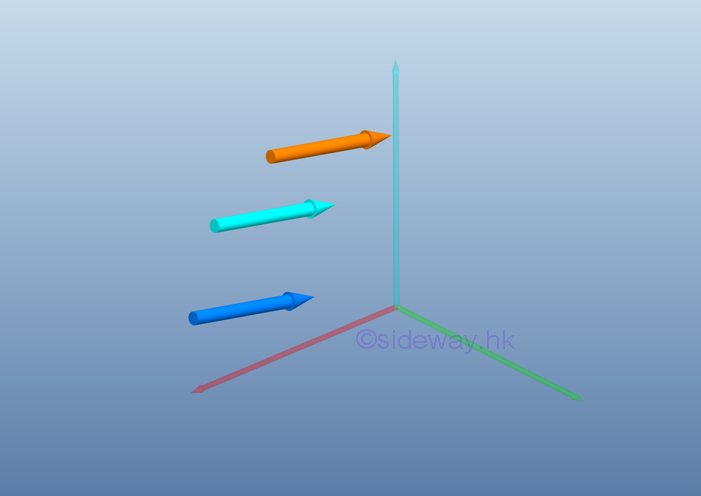
Types of System of ForcesIn general, forces can be classified according to its point of application and line of action. Concurrent forces are forces that are applied at the same point. While non concurrent forces are system of forces without a common point of application.
Coplanar forces are forces with line of actions that are in the same plane. When forces with line of actions that are not in a single plane, they are non coplanar forces in space.
Parallel forces are forces with line of actions that are parallel to each other. When system of forces contain force with line of actions are not parallel to others, they are non parallel forces.
And the special case, collinear forces are forces with line of actions that are applied along the same line.
Different types of system of forces can be grouped by the combination of classes of forces, Concurrent forces can be coplanar or non coplanar. Coplanar concurrent forces system contains forces which met at a single point and lie in a single plane.
While non coplanar concurrent forces system contains spatial forces which met at a single point but their line of actions do not lie in the same plane.
Similarly, non concurrent forces can also be coplanar or non coplanar. Coplanar non concurrent forces system contains forces which do not pass through the same point but their line of actions lie in a single plane.
While non coplanar non concurrent forces system contains spatial forces which do not pass through the same point and their line of actions do not lie in the same plane also.
Parallel forces are the special case of non concurrent forces. Parallel forces can also be coplanar or non coplanar. Coplanar parallel forces system contains forces with line of actions are parallel to each other and lie in the same plane.
While non coplanar parallel forces system contains forces with line of actions are parallel to each other but they are not in the same plane.
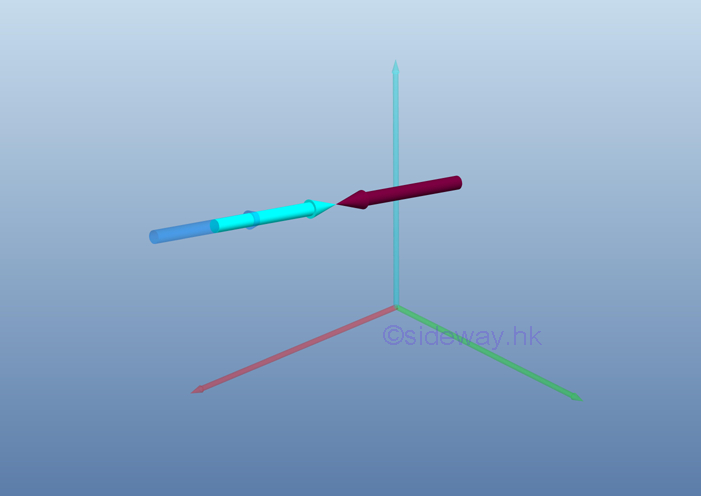
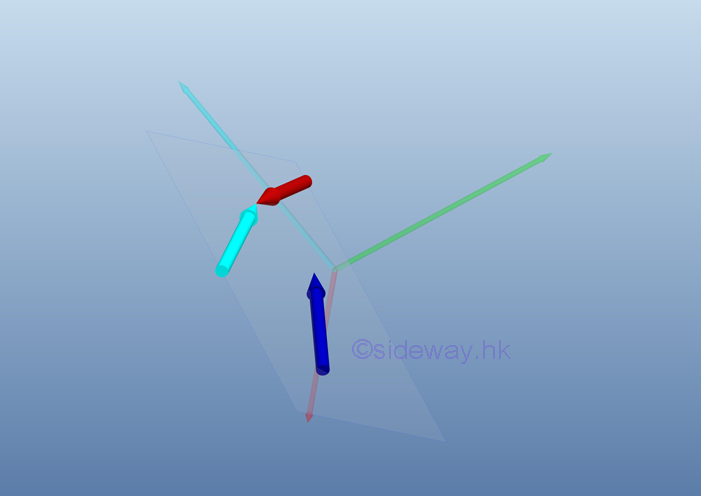
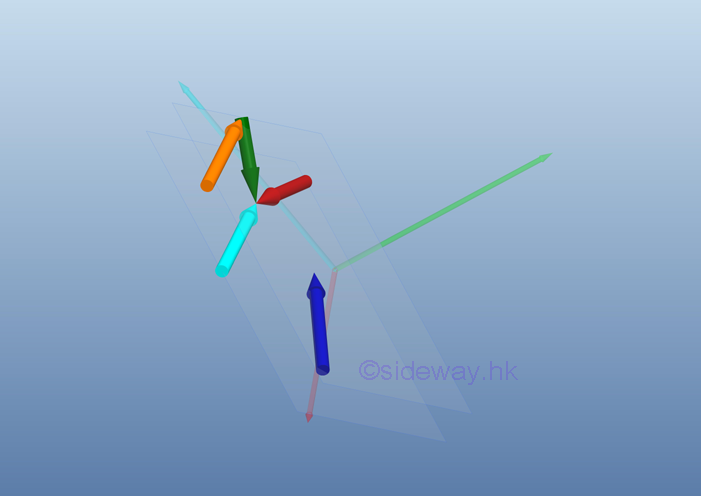
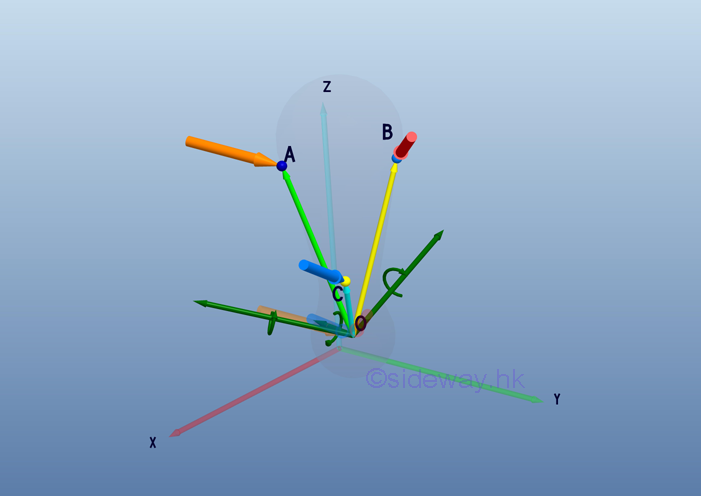
Link:http://output.to/sideway/default.asp?qno=110700014 Equivalent systems of forces System of Forces ReductionWhen a force system consists of more than one force, the system of forces should be reduced to one force and one couple. System of forces, F1, F2, and F3 acting on a rigid body at points, A, B, and C, respectively can be transformed to the point of interest, O through force vector transformation,
According to force vector transformation, forces at different points of application can be moved to the point of interest, O. And the moments of forces about the point of interest, O can also be determined by the cross product of the moment arm of each force vector and the force vector.
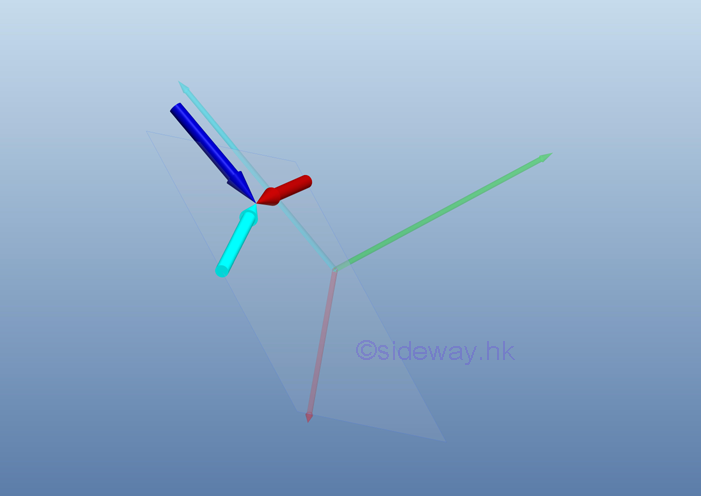
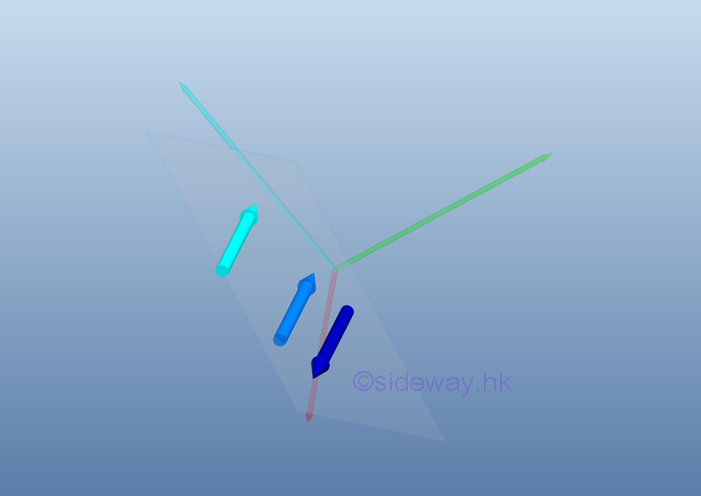
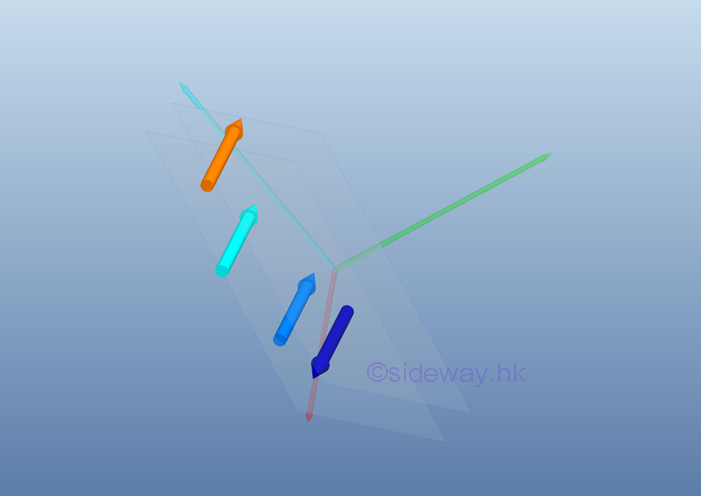
After all force vectors are moved to point O and all moment vectors are replaced by couple vectors. The equivalent system acting at a point O on a rigid body can be determined by the vector sum of the all force vectors and the vector sum of all couple vectors at the point O. 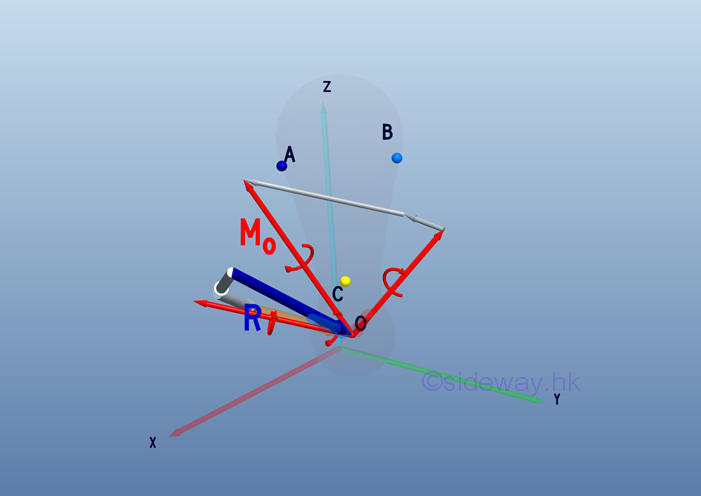
Therefore, a system of force can be reduced to an equivalent force-couple system consists of a force vector R and a couple vector MO.
Mathematically, the force vector R and the couple vector MO of equivalent system consists can be expressed as:
The equivalent force-couple system can then be further transferred to other points of interest through the force-couple system transformation. Vector DecompositionThe resultant force vector and resultant couple vector can be determined in terms of rectangular compontents through vector decomposition. Imply the force vector and moment arm vector equal to:
And the resultant force vector and couple vector equal to:
The resultant force vector equal to:
Imply:
The resultant couple vector equal to:
where: 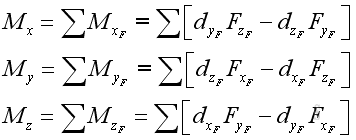
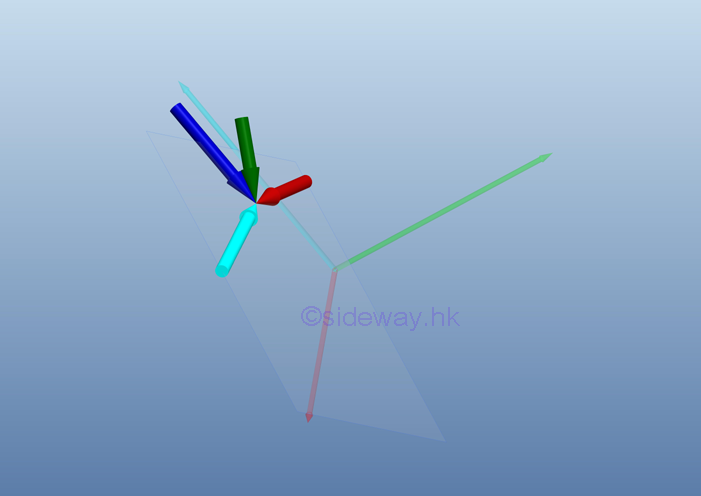
Equivalent Systems of ForcesTherefore two systems of forces are equivalent at the point of interest, if:
Or in terms of rectangular components:
Types of Equivalent Systems of ForcesThe two elements of an equivalent force-couple system at O are a resultant force vector R and a resultant couple vector MO at O.
|
Sideway BICK Blog 12/07 |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
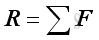 and
and
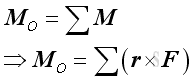
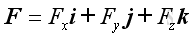 and
and
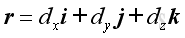
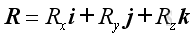 and
and
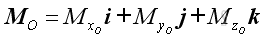
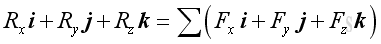
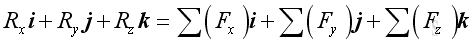
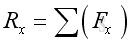
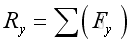
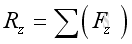
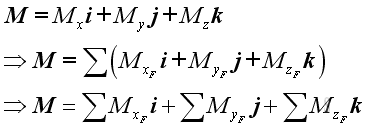 .
.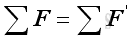 and
and
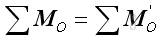
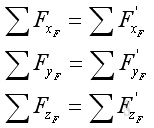 and
and