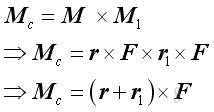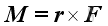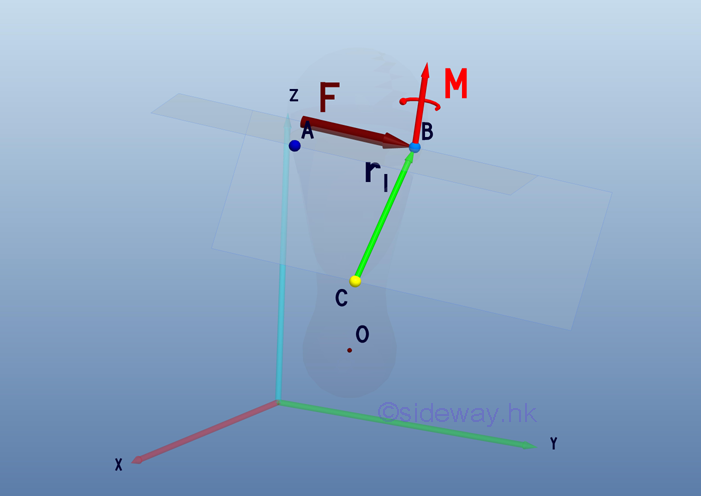
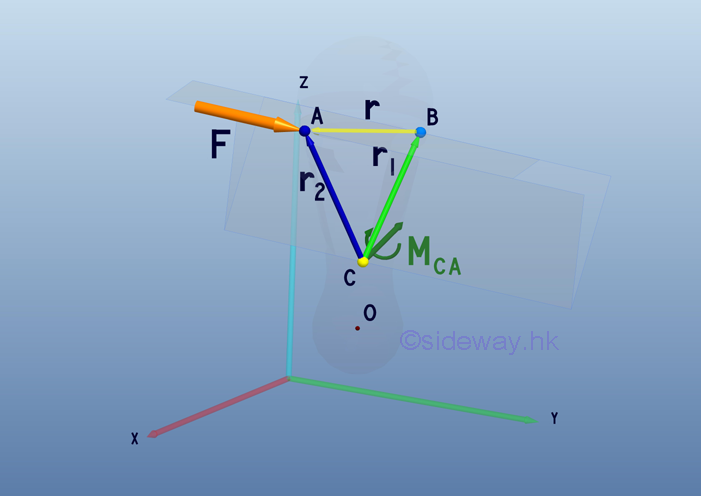
Force-Couple system

Sometime the applied point of a force-couple system is also need to be considered at a different point. When the above force-couple system at point B is to be considered at point C, both the force and couple vectors are needed to be considered.

 

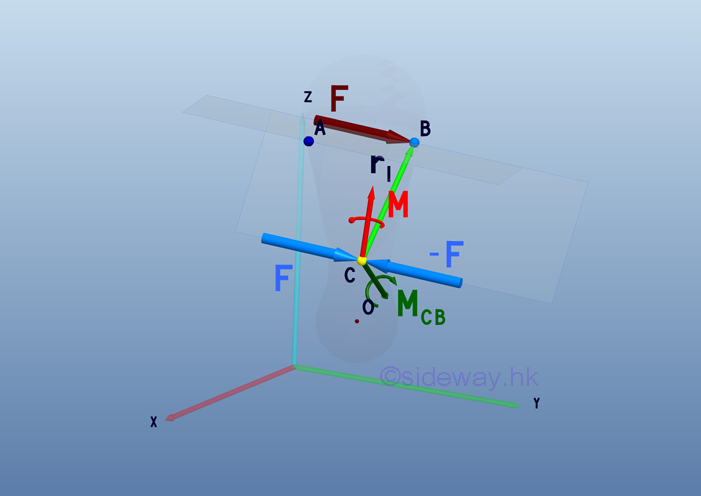
Since couple vector is a free vector, the couple vector M can be attached to point C directly without making any change. For the force vector, it can be treated as a single force transformation by attaching two forces, F and -F with magnitude equal to the applied force F at point C as before. But when the force F is applied at point B on the rigid body, the moment of the force about point C is equal to  MCB . 

 

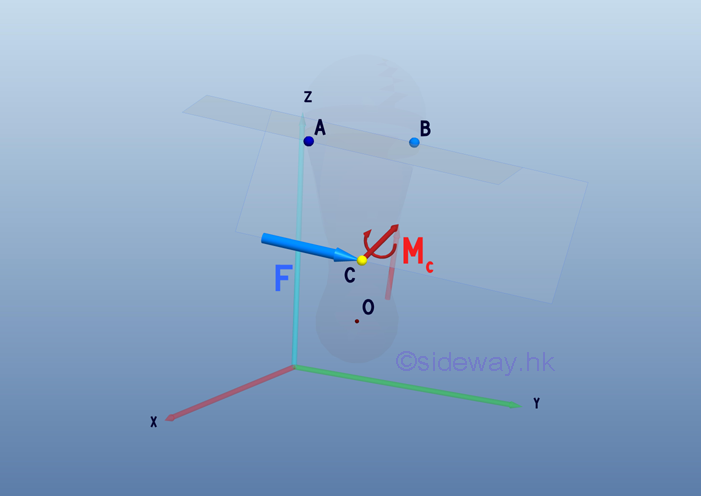
The formed force couple of moment MCB can be replaced by a couple vector M1. The couple vector M1 is a free vector and it can be located at point C for convenience.  Two couple vectors are then added to form a resultant couple vector  Mc.

 

Therefore the equivalent system of a force-couple system acting at point B on a rigid body can be transformed to an arbitrary point C by moving both the force vector F and the couple vector M to point C, and adding a couple vector M1 with moment equals to the moment MCB of the force vector F at point B about point C. At which, the force vector F tend to provide the same linear motion and the resultant couple vector Mc tend to provide the same rotational motion as the force vector F at point B. The equivalent system is also force-couple system.

 

And the resultant couple or moment vector can be expressed as:

 

When considering the moment of force F at point A about point C,  the moment is equal to MCA .

 

And the moment vector can be expressed as: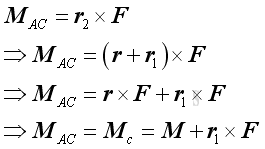

Since the force vector F can also be moved to point C as in the force transformation, the results of two system transformation are equal. Therefore the equivalent system of a force-couple system acting can be transformed from point B to an arbitrary point C by moving both the force vector F and the couple vector M to point C, and adding a couple vector M1 with moment equals to the moment MCB of the force vector F at point B about point C.

 

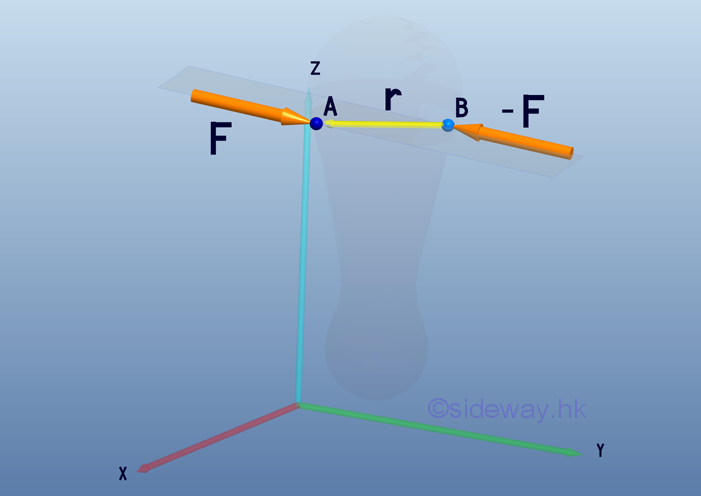
System of Forces Transformation

Sometimes a system of forces acting on a rigid body is needed to be transformed into an equivalent system at the point of interest.

Force Couple

A couple of force F is applied at points A, B on a rigid body.

 

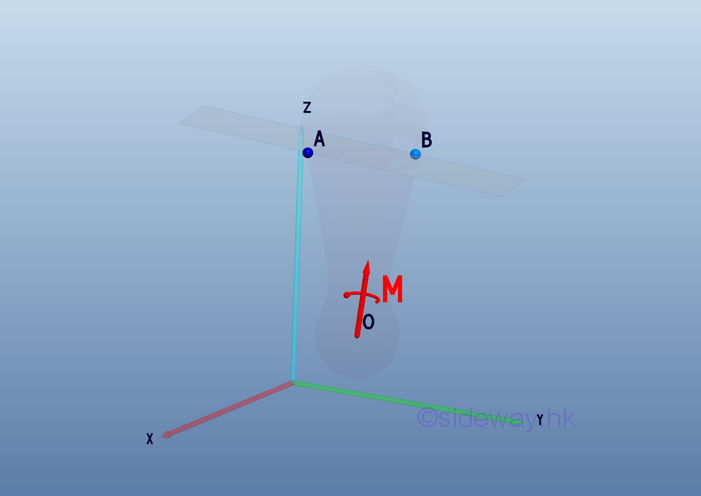
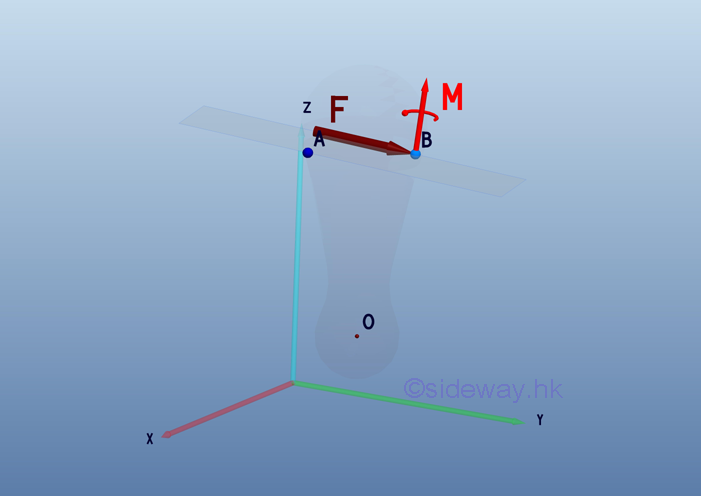
The equivalent system is a free couple vector M acting on any location of the rigid body.

 

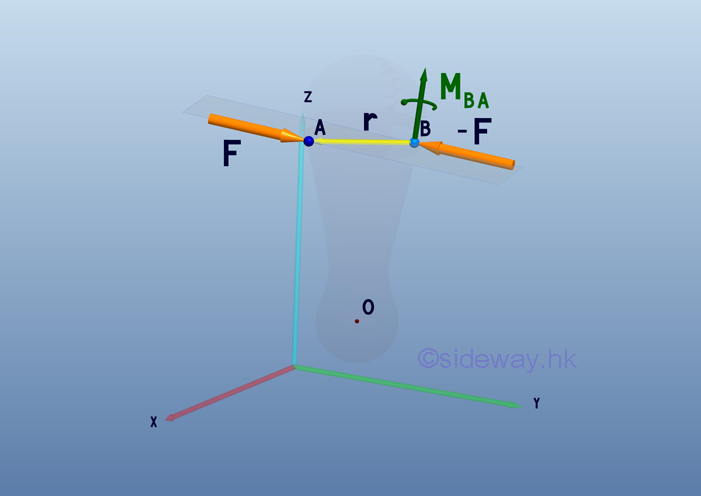
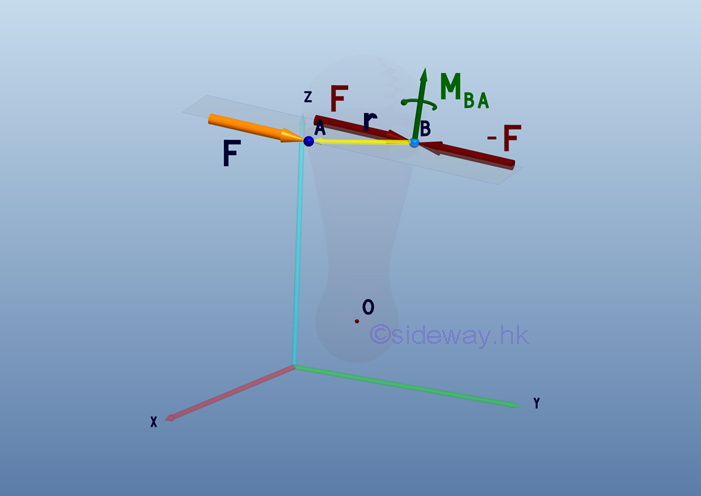
Consider the moment MBA at point B,  the tendency of rotation above B is caused by the applied force F at A. The applied force -F at B can be considered as the reaction supporting force. Both the magnitude and direction of the moment vector MBA  is same as the couple vector M.

 

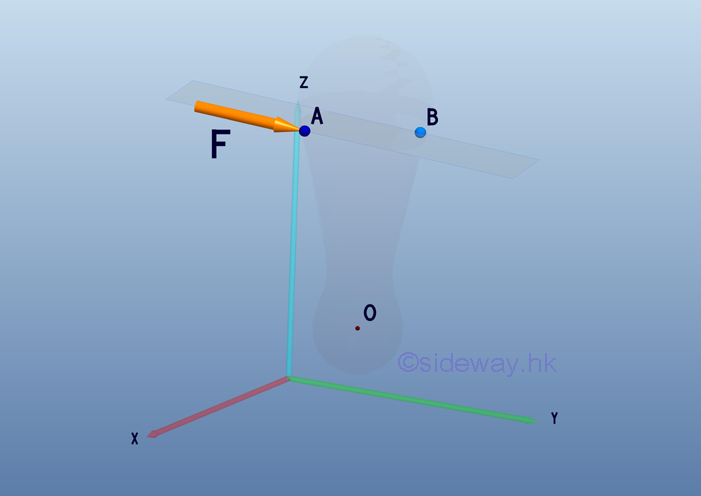
Force Vector

Suppose a force vector acting at point A on the rigid body is to be considered at point B.

 

When only a single force F is applied at point A on the rigid body, the moment of the force at point A about point B is also equal to  MBA .

 

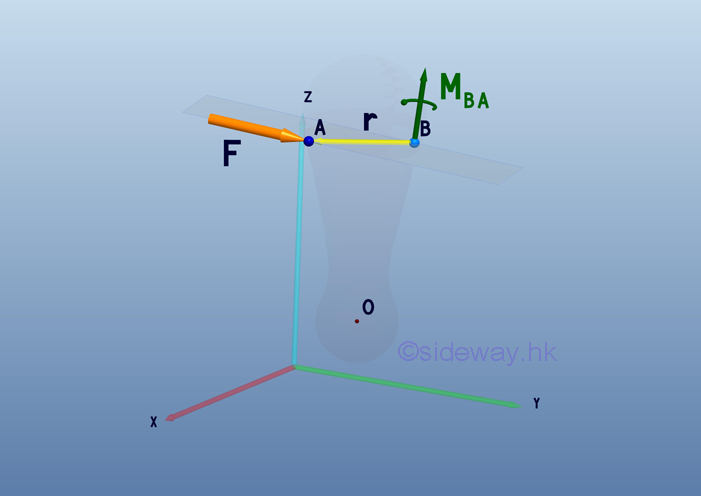
To simulate the force couple condition, two forces, F and  -F with magnitude equal to the applied force F are attached at point B. After this transformation, a force couple of moment MBA is formed with an additional force -F acting at point B.

 

Force F acting at point A is now moved to point B. The formed force couple of moment MBA can be replaced by a couple vector M. The couple vector M is a free vector and it can be located at point B for convenience.

 

Therefore the equivalent system of a force vector F acting at point A on a rigid body can be transformed to an arbitrary point B by moving the force vector to pont B and adding a couple vector M with moment equals to the moment MBA of the force vector F about point B. At which, the force vector F tend to provide the same linear motion and the couple vector M tend to provide the same rotational motion as the force vector F at point A. The equivalent system of combining a force vector and a couple vector is named as force-couple system. And the couple vector is