Average of Accumulative Physical Quantity

The average value of a continuous variable is one of the special case of the weighted average of a continuous variable when the weighting of all possible values are equal. In general, a weighted average of accumulative physical quantity can be determined by integration if the physical quantity can be expressed as a function of the interested weighting and quantified in the form of  infinitesimal elements. imply

Centrod and Center of Mass/gravity

Centrod of an object is the geometric center of the object shape on which the object is geometrically balanced. And the center of gravity or center of mass is related to gravitation and the density function of the object. The coordinates of the center point can be determined by moment about a axis by equating  the corresponding moment of all the elemental weights about the axis equal to the moment of the whole object about the axis. Imply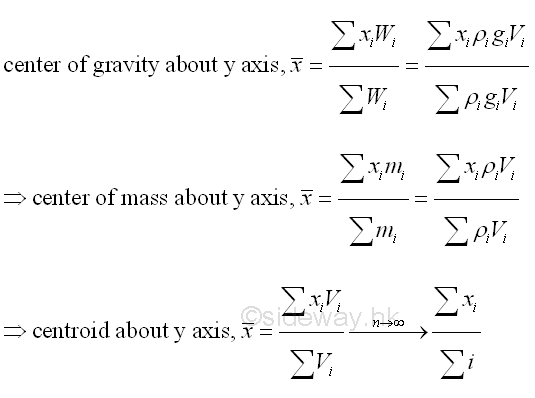

Centrod of a Curve

When the cross-sectional area of an object is neglectable, the centroid of the object depends on its shape and the centroid is reduced to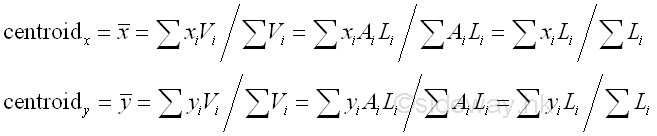

Centroid of a horizontal straight wire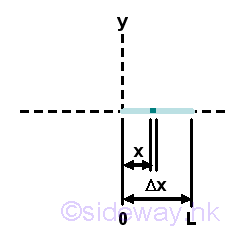

For a horizontal straight wire, the moment about x axis is zero, imply mean y is zero. Imply mean x is

Centroid of a sloped straight wire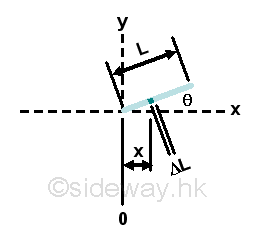

For a sloped straight wire, Imply mean x is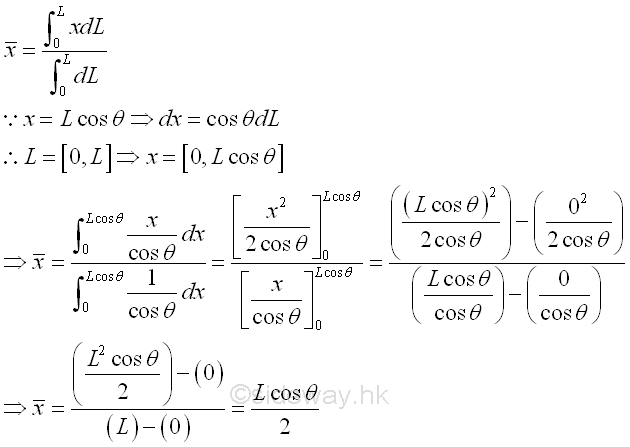

For a sloped straight wire, Imply mean y is

Centroid of a Semicircular arc wire

For a circular wire, the centroid is equal to the center of the circle. But for a horizontal semicircular arc with centre at the origin, the moment about y axis is zero, imply mean x is zero. Imply mean y is

Express y in terms of θ. Imply mean y is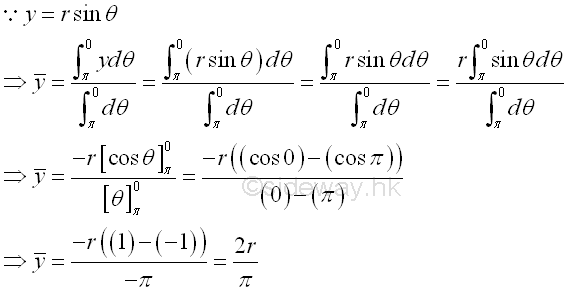

Centroid of a Quarter-circular arc wire

For a quarter-circular wire, the centroid is symmetry about the angle bisector, the moments about x axis and y axis are the same. imply mean x equal to mean y and is equal to

Centroid of a circular arc wire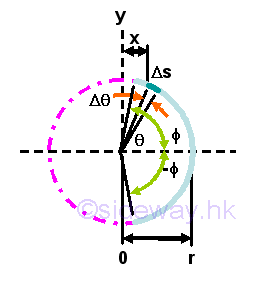

For a circular arc wire, the centroid is symmetry about the angle bisector, x axis. The moments about x axis is zero, imply mean y is zero. Imply mean x is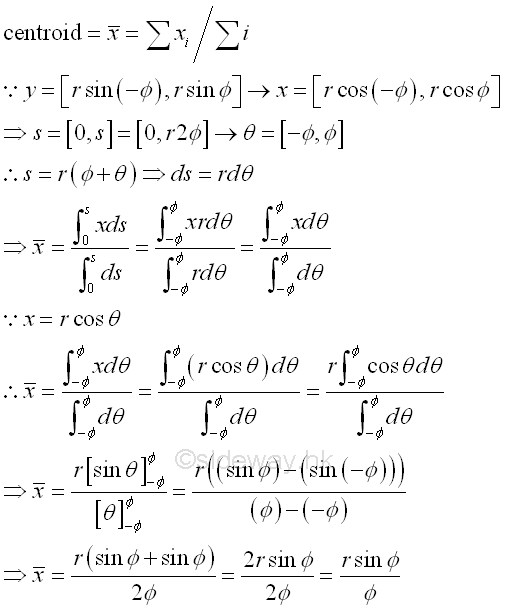

Average of Accumulative Physical Quantity

In general, a weighted average of accumulative physical quantity can be determined by integration if the physical quantity can be expressed as a function of the interested weighting and quantified in the form of  infinitesimal elements. Besides the centroid of a curve, the centroid of an area can also determined by integration also.

Centrod of an Area

For an flat houmogeneous plate with uniform thickness, the centroid of the plate depends on its shape and the centroid is reduced to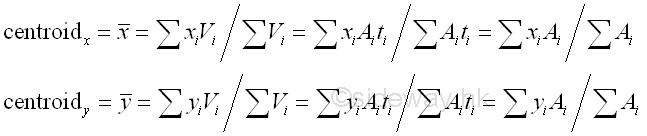

Centroid of a Triangular area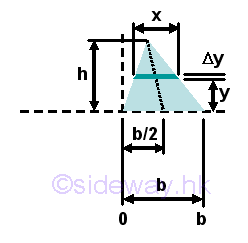

For a triangular area with base b and height h, the moment along x axis direction is zero about the median, imply mean x lies on the median. For mean y is

Centroid of a Semicircular Area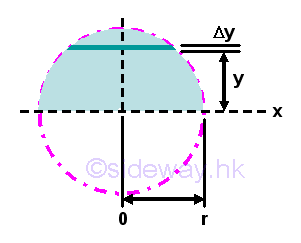

For a semicircular area, due to symmetry about y axis,the centroid lies on the y axis. Imply mean y is

Centroid of a Quarter-circular area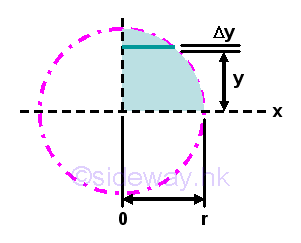

For a quarter-circular area, the centroid is symmetry about the angle bisector, the moments about x axis and y axis are the same. imply mean x equal to mean y and is equal to

Centroid of a circular arc area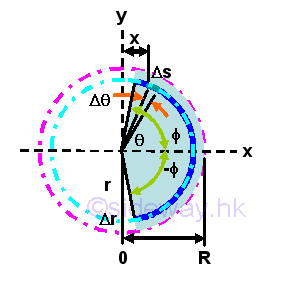

For a circular arc area, the centroid is symmetry about the angle bisector, x axis. The moments about x axis is zero, imply mean y is zero. The determination of mean x can make use of the moment of a circular arc wire. Imply mean x is