 Sideway
BICK BLOG from Sideway
Sideway
BICK BLOG from Sideway
|
Link:http://output.to/sideway/default.asp?qno=120100015 Geometrical Approximation of Length of a Function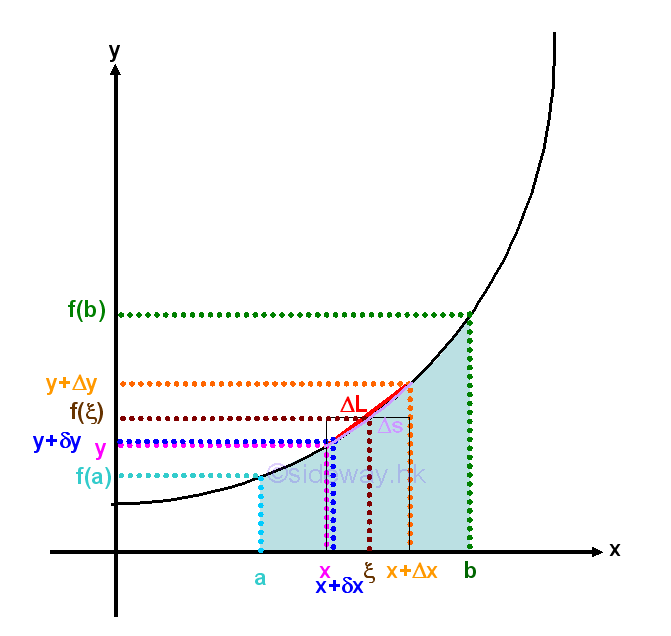
In general, the integral of a function is the approximation of the sum of function over a closed interval . 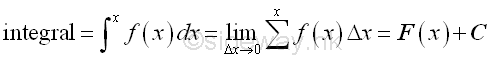
When Δx approaching zero, the limit exist and the integral converges to its instantaneous function with respect to the variable of integration. As Δx approaching zero, the length Δs of a function can also be approximated by the secant line ΔL of the infinitesimal curve element. Geometrically, the slope of the secant line is equal to the derivative of the function. Imply 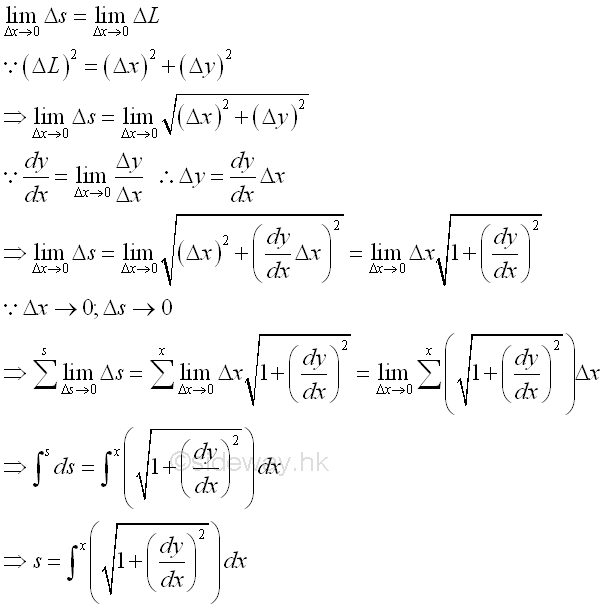
Curve Length of a FunctionTherefore the curve length of a function over a closed interval can be determined by integration. For example, y=x3/2 [0,1] Graphically, 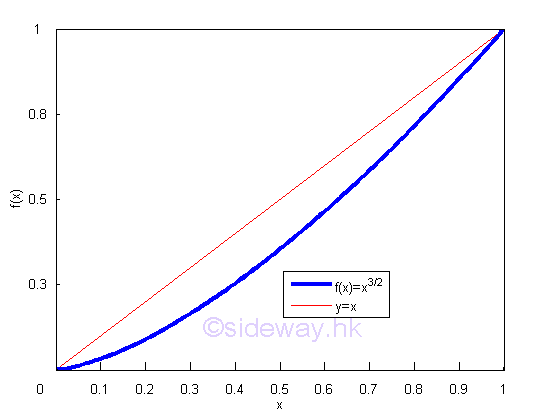
The curve length of function over a closed interval is 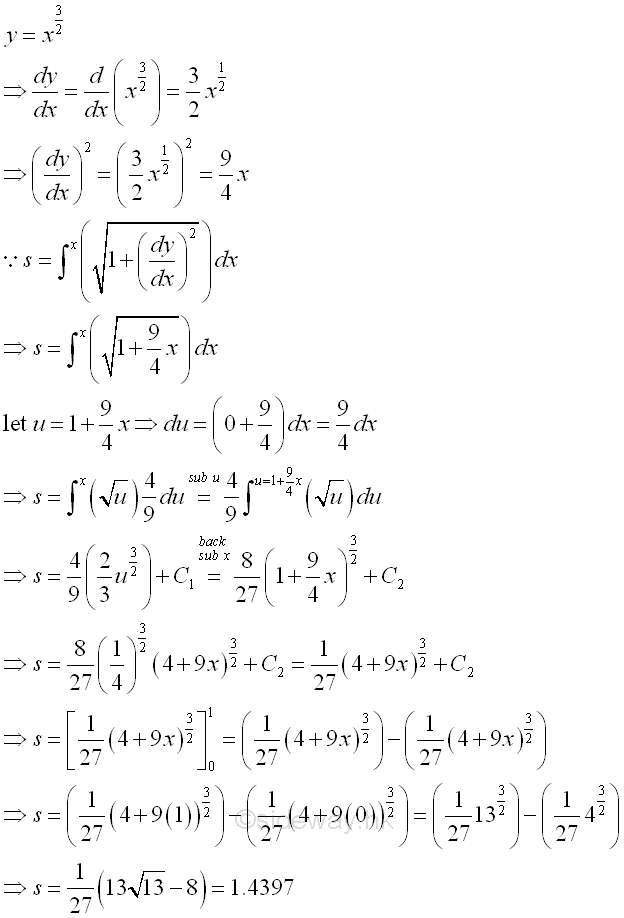
|
Sideway BICK Blog 13/01 |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||

