 Sideway
BICK BLOG from Sideway
Sideway
BICK BLOG from Sideway
|
Link:http://output.to/sideway/default.asp?qno=120500016 Centroid of Plane Body Centroid of 2D Plane BodyThe centroid of an plate is determined by the first moment of a two dimensional plane body with the method of the first moment of area. 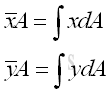
And the centroid of a wire is determined by the first moment of a two dimensional plane body with the method of the first moment of line. 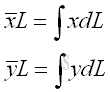
Centroids of AreasArea by IntegrationArea by Double Integration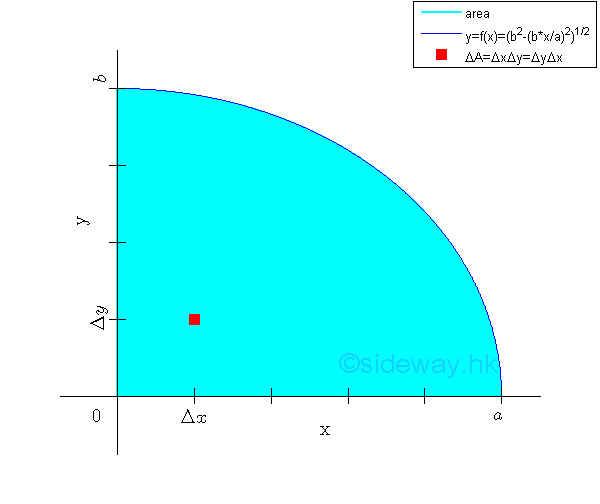
For example, the signed area of the planar region R is bounded by curves in rectangular form , Imply 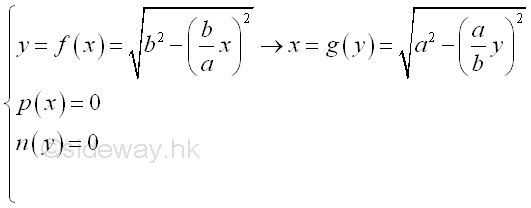
An elemental area ΔA in rectangular form can be defined as Δx times Δy. Imply 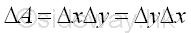
In general, the area of a region can be determined by multiple integration through sweeping the signed elemental area starting from along either rectangular coordinate axis. Imply Starting from horizontal sweeping along x axis 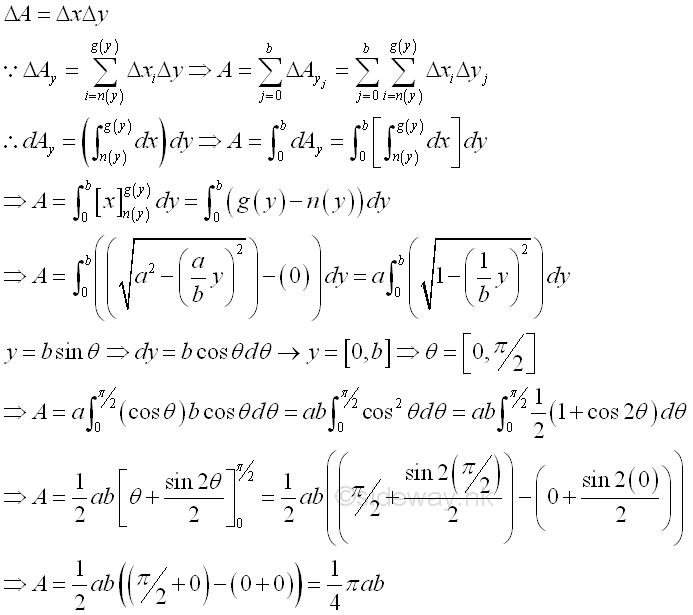
Starting from vertical sweeping along y axis 
And for curves in polar form 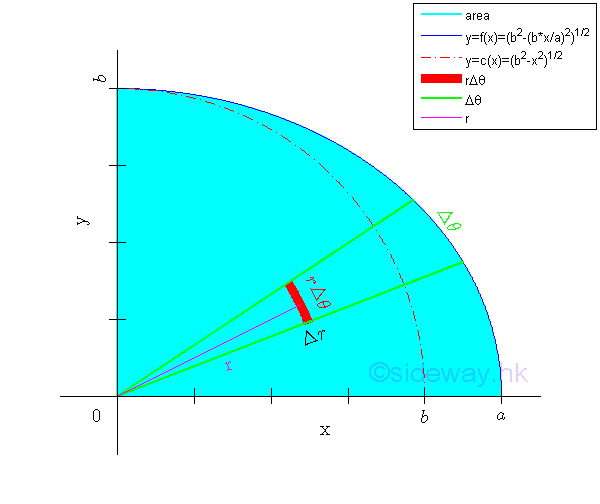
For example, the signed area of the planar region R is bounded by curves in polar form , For the curve profile, Imply 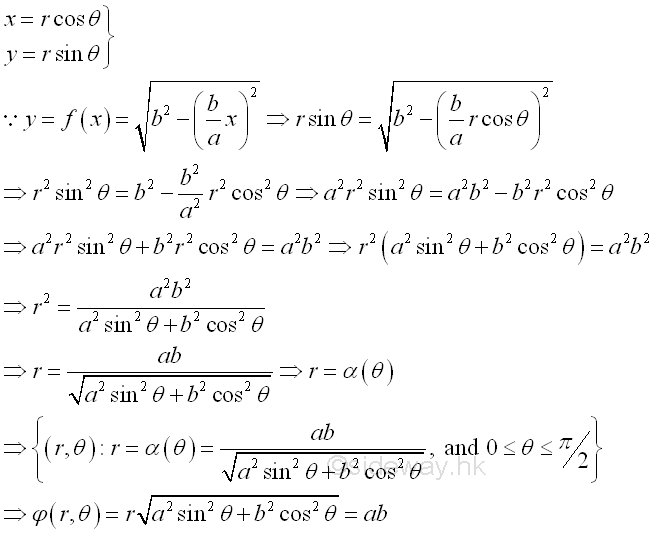
And the curve profile in terms of θ, imply 
And other boundary curves are 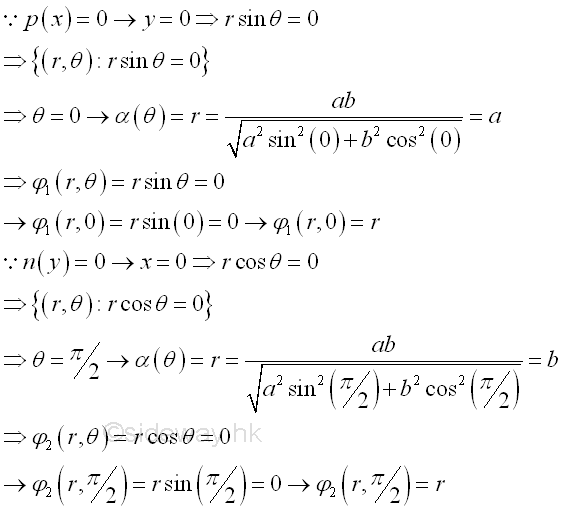
An elemental area ΔA in polar form can be approximated by Δr times rΔθ. Imply 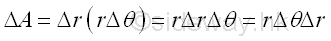
Unlike rectangular form, the polar form of an elemental area ΔA is not a constant but a function of r and in turn a function of θ also. In general, the area of a region can be determined by multiple integration through sweeping the signed elemental area starting from along either polar variables. Imply Starting from radical sweeping along variable radius r 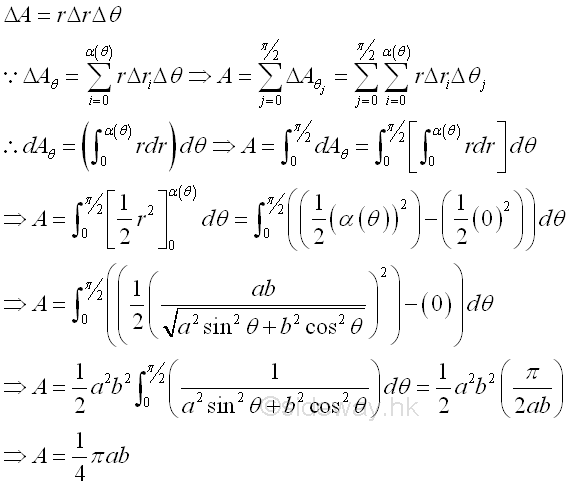
Starting from circular sweeping along variable angle θ, 
|
Sideway BICK Blog 30/05 |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||

