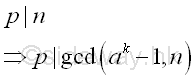Sideway
BICK BLOG from Sideway
Sideway
BICK BLOG from Sideway
|
Link:http://output.to/sideway/default.asp?qno=120500006 Pollard's p-1 Method Pollard's p-1 MethodPollard's p-1 method is a prime factorization algorithm discovered by John Pollard in 1974. Limited by the algorithm, the Pollard's p-1 method is only work for integers with specific factors. If the number n has a prime factor p such that p-1 can be expressed in terms of a product of primes, the finding of prime factor p is based on the selected boundary B of the B-smooth number. The algorithm fails when the selected boundary B is smaller than the B-smooth number of p-1. Pollard's P-1 Methed by Smooth NumberPollard's P-1 Methed by Smooth Number Example 2For example: n=667=p*q=23*29; let B=5 imply
Therefore for B=5, k5 or (p5-1)m5 is equal to 77760000. Fermat's Little Theoremlet a=2, by Fermat's little theorem, let p be one of the prime factors of n, imply p idivides ak-1. 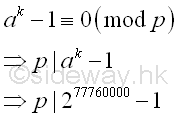
Greatest Common DivisorSince ak-1 is a very large number, before finding the greatest common divisor of n and ak-1, ak-1 can be raised to the high power modulo n. Imply Using squarings modulo
and using the residue to calculate the greatest common divisor. Imply 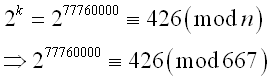
The greatest common divisor of n and ak-1 is Using Euclid's algorithm
Imply 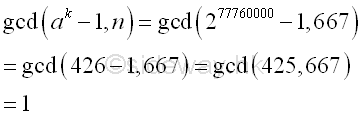
The algorithm fails because the greatest common divisor of n and ak-1 is equal to 1. The number n does not have prime divisor p with p-1 is 5-smooth. Therefore the bound B equals to 5 fails, a larger bound B' should be used. Let B=7, imply
Therefore for B=7, k7 or (p7-1)m7 is equal to 77760000*343 = 26671680000. Imply k7 = k5 * 343. And the new ak can be expressed as 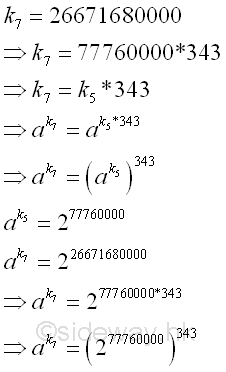
And ak can be raised to the high power modulo n, imply 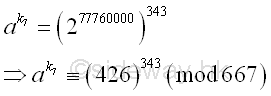
Using squarings modulo
and using the residue to calculate the greatest common divisor. Imply 
The greatest common divisor of n and ak-1 is Using Euclid's algorithm
Imply 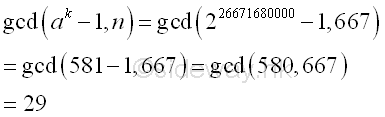
Integer 29, the greatest common divisor of n and ak-1 is also the prime divisor of n. And p-1 is 7-smooth.
Link:http://output.to/sideway/default.asp?qno=120500004 Pollard's p-1 Method Pollard's p-1 MethodPollard's p-1 method is a prime factorization algorithm discovered by John Pollard in 1974. Limited by the algorithm, the Pollard's p-1 method is only work for integers with specific factors. Pollard's p-1 AlgorithmFor a composite integer, n, with a prime factor p, if p-1 can be expressed in terms of a product of primes and k is a multiple of p-1. By selecting an integer, a, which is greater than 1 and is coprime to n, then
Imply
Since a is coprime to n, a is coprime to p also. Imply
From Fermat's little theorem, if p does not divide a, then 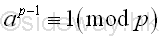
Similarly, If k is a multiple of p-1, then 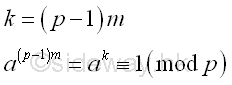
Imply p is a non-trivial divisor of ap-1-1 or ak-1 .
Since p is also a prime factor of n, p divides the greatest common divisor of ap-1-1 or ak-1, and n.
Therefore, if the greatest common divisor of ak-1, and n is greater than 1, the greatest common divisor is a factor of n also. Pollard's p-1 MethodAlthough the Pollard's p-1 algorithm cannot be used to determine the prime factor p directly, the Pollard's p-1 method is an efficient prime factor finding method for composite integers with specific types of prime factors by choosing and testing some integers systematically. Smooth Number MethodSmooth NumberOne of the number choosing method for integer k is the making use of the concept of smooth number and the specific type of prime factor, i.e. p-1 is the product of primes. Let x and B be integers. x is said to be B-smooth if all the prime divisors of n are less than or equal to B. 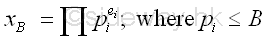
Example of Smooth Number
Although B is usually a prime number, B can be a composite number providing that B is greater than or equal to the largest prime factor of x. The key information from a B-smooth number is the prime factor of a number. However, there is no information on the power or index of the prime factor. The lowest B-smooth of a number is the greatest prime factor of the number. Pollard's P-1 Methed by Smooth NumberSince p-1 divides k, by assuming p-1 is B-smooth, if k is also B-smooth then the choosen integer k should be sufficienly large to ensure p-1 divides k. Therefore k is the product of all prime factors with powers less than and equal to B and the index or power ei for each prime factor pi less than and equal to B of k should be just less than and equal to n. Imply 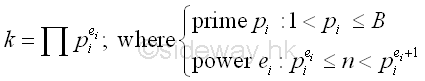
Pollard's P-1 Methed by Smooth Number Example 1For example: n=203=p*q=7*29; let B=5 imply
Therefore for B=5, k5 or (p5-1)m5 is equal to 1296000. Fermat's Little Theoremlet a=2, by Fermat's little theorem, let p be one of the prime factors of n, imply 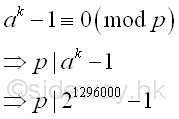
Greatest Common DivisorSince ak-1 is a very large number, before finding the greatest common divisor of n and ak-1, ak-1 can be raised to the high power modulo n. Imply Using squarings modulo
Using binary squarings modulo
and using the residue to calculate the greatest common divisor. Imply 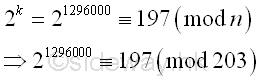
The greatest common divisor of n and ak-1 is Using Euclid's algorithm
Imply 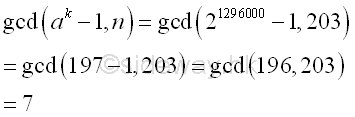
Integer 7, the greatest common divisor of n and ak-1 is also the prime divisor of n. And p-1 is 5-smooth.
Since the greatest prime factor of p-1 is 3-smooth also. And therefore the prime factor 7 can also be found by using B=3
let a=2, by Fermat's little theorem, imply p divides 210368-1 ≡ 168 (mod 203) The greatest common divisor of n and ak-1 is gcd(168,203)= 7 And 7 is the prime divisor of n as before. |
Sideway BICK Blog 11/05 |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
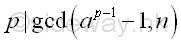
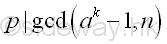
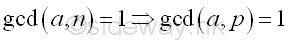
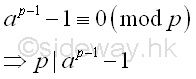 or
or 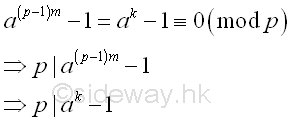
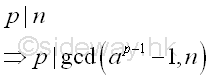 or
or