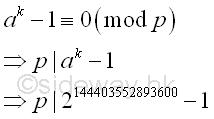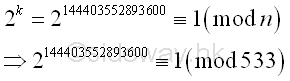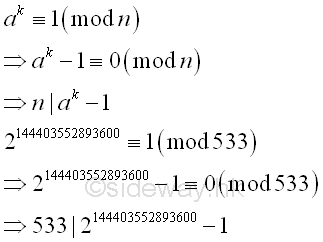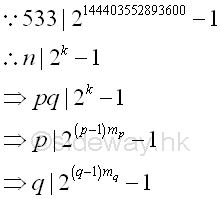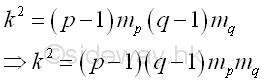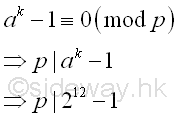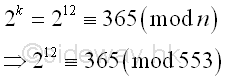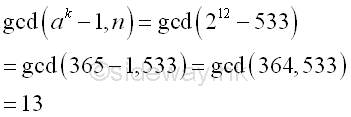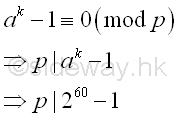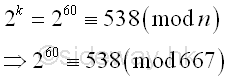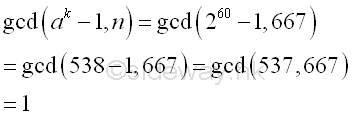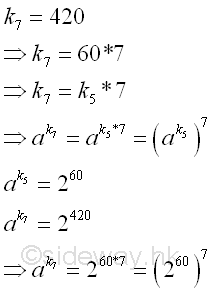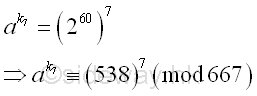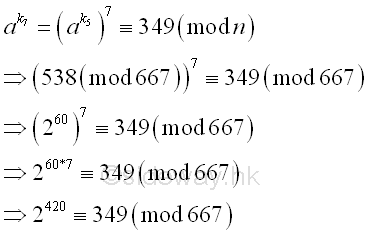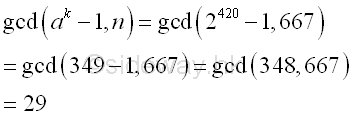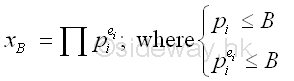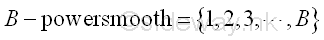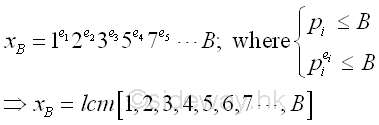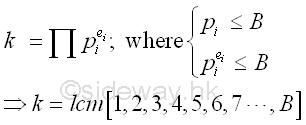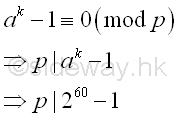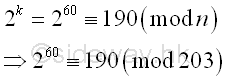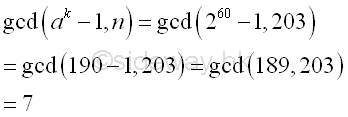|
Link:http://output.to/sideway/default.asp?qno=120500011 Pollard's p-1 Method
Pollard's p-1 Method
Pollard's p-1 method is a prime factorization algorithm
discovered by John Pollard
in 1974. Limited by the algorithm, the Pollard's p-1 method is only work for
integers with specific factors.
However, since the composite number n is an unknown, sometimes, the algorithm
may return a false response.
Characteristic of Pollard's p-1 Method by
PowerSmooth Number
The advantage of Pollard's p-1 method by
powersmooth number is the checking of a
group of primes with one computation. Every boundary B represents a group
of numbers that can be expressed as the product of prime power factors less than and
equal to number B.
For example, a composite number n less than 10000 should have a prime factor
less than √n=100. And primes within 100 are
| Primes |
Integer |
B -
power smooth |
count |
LCM[1,...,B] |
| 2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47,
53, 59, 61, 67, 71, 73, 79, 83, 89, 97 |
p |
|
25 |
|
| 2, 3 |
p-1 |
2 |
2 |
2 |
| 2, 3, 7 |
p-1 |
3 |
3 |
6 |
| 2, 3, 7, 13 |
p-1 |
4 |
4 |
12 |
| 2, 3, 5, 7, 11, 13, 31, 61 |
p-1 |
5 |
8 |
60 |
| 2, 3, 5, 7, 11, 13, 31, 61 |
p-1 |
6 |
8 |
61 |
| 2, 3, 5, 7, 11, 13, 29, 31, 43, 61, 71 |
p-1 |
7 |
11 |
420 |
| 2, 3, 5, 7, 11, 13, 29, 31, 41, 43, 61, 71 |
p-1 |
8 |
12 |
840 |
| 2, 3, 5, 7, 11, 13, 19, 29, 31, 37, 41, 43, 61, 71, 73 |
p-1 |
9 |
15 |
2520 |
| 2, 3, 5, 7, 11, 13, 19, 29, 31, 37, 41, 43, 61, 71, 73 |
p-1 |
10 |
15 |
2520 |
| 2, 3, 5, 7, 11, 13, 19, 23, 29, 31, 37, 41, 43, 61, 67,
71, 73, 89 |
p-1 |
11 |
18 |
27720 |
| 2, 3, 5, 7, 11, 13, 19, 23, 29, 31, 37, 41, 43, 61,
67, 71, 73, 89 |
p-1 |
12 |
18 |
27720 |
| 2, 3, 5, 7, 11, 13, 19, 23, 29, 31, 37, 41, 43, 53, 61,
67, 71, 73, 79, 89 |
p-1 |
13 |
20 |
360360 |
| 2, 3, 5, 7, 11, 13, 19, 23, 29, 31, 37, 41, 43, 53,
61, 67, 71, 73, 79, 89 |
p-1 |
14 |
20 |
360360 |
| 2, 3, 5, 7, 11, 13, 19, 23, 29, 31, 37, 41, 43, 53,
61, 67, 71, 73, 79, 89 |
p-1 |
15 |
20 |
360360 |
| 2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 53,
61, 67, 71, 73, 79, 89 |
p-1 |
16 |
21 |
720720 |
| 2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 53,
61, 67, 71, 73, 79, 89 |
p-1 |
17 |
21 |
12252240 |
| 2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 53,
61, 67, 71, 73, 79, 89 |
p-1 |
18 |
21 |
12252240 |
| 2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 53,
61, 67, 71, 73, 79, 89 |
p-1 |
19 |
21 |
232792560 |
| 2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 53,
61, 67, 71, 73, 79, 89 |
p-1 |
20 |
21 |
232792560 |
| 2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 53,
61, 67, 71, 73, 79, 89 |
p-1 |
21 |
21 |
232792560 |
| 2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 53,
61, 67, 71, 73, 79, 89 |
p-1 |
22 |
21 |
232792560 |
| 2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47,
53, 61, 67, 71, 73, 79, 89 |
p-1 |
23 |
22 |
5354228880 |
| 2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47,
53, 61, 67, 71, 73, 79, 89 |
p-1 |
24 |
22 |
5354228880 |
| 2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47,
53, 61, 67, 71, 73, 79, 89 |
p-1 |
25 |
22 |
26771144400 |
| 2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47,
53, 61, 67, 71, 73, 79, 89 |
p-1 |
26 |
22 |
26771144400 |
| 2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47,
53, 61, 67, 71, 73, 79, 89 |
p-1 |
27 |
22 |
80313433200 |
| 2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47,
53, 61, 67, 71, 73, 79, 89 |
p-1 |
28 |
22 |
80313433200 |
| 2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47,
53, 59, 61, 67, 71, 73, 79, 89 |
p-1 |
29 |
23 |
2329089562800 |
| 2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47,
53, 59, 61, 67, 71, 73, 79, 89 |
p-1 |
30 |
23 |
2329089562800 |
| 2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47,
53, 59, 61, 67, 71, 73, 79, 89 |
p-1 |
31 |
23 |
72201776446800 |
| 2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47,
53, 59, 61, 67, 71, 73, 79, 89, 97 |
p-1 |
32 |
24 |
144403552893600 |
| 2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47,
53, 59, 61, 67, 71, 73, 79, 89, 97 |
p-1 |
33 |
24 |
144403552893600 |
| 2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47,
53, 59, 61, 67, 71, 73, 79, 89, 97 |
p-1 |
34 |
24 |
144403552893600 |
| 2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47,
53, 59, 61, 67, 71, 73, 79, 89, 97 |
p-1 |
35 |
24 |
144403552893600 |
| 2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47,
53, 59, 61, 67, 71, 73, 79, 89, 97 |
p-1 |
36 |
24 |
144403552893600 |
| 2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47,
53, 59, 61, 67, 71, 73, 79, 89, 97 |
p-1 |
37 |
24 |
144403552893600 * 37 |
| 2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47,
53, 59, 61, 67, 71, 73, 79, 89, 97 |
p-1 |
38 |
24 |
144403552893600 * 37 |
| 2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47,
53, 59, 61, 67, 71, 73, 79, 89, 97 |
p-1 |
39 |
24 |
144403552893600 * 37 |
| 2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47,
53, 59, 61, 67, 71, 73, 79, 89, 97 |
p-1 |
40 |
24 |
144403552893600 * 37 |
| 2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47,
53, 59, 61, 67, 71, 73, 79, 83, 89, 97 |
p-1 |
41 |
25 |
144403552893600 * 37 * 41 |
| 2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47,
53, 59, 61, 67, 71, 73, 79, 83, 89, 97 |
p-1 |
42 |
25 |
144403552893600 * 37 * 41 |
| 2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47,
53, 59, 61, 67, 71, 73, 79, 83, 89, 97 |
p-1 |
43 |
25 |
144403552893600 * 37 * 41 * 43 |
| 2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47,
53, 59, 61, 67, 71, 73, 79, 83, 89, 97 |
p-1 |
44 |
25 |
144403552893600 * 37 * 41 * 43 |
| 2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47,
53, 59, 61, 67, 71, 73, 79, 83, 89, 97 |
p-1 |
45 |
25 |
144403552893600 * 37 * 41 * 43 |
| 2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47,
53, 59, 61, 67, 71, 73, 79, 83, 89, 97 |
p-1 |
46 |
25 |
144403552893600 * 37 * 41 * 43 |
| 2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47,
53, 59, 61, 67, 71, 73, 79, 83, 89, 97 |
p-1 |
47 |
25 |
144403552893600 * 37 * 41 * 43
* 47 |
More primes can be included for checking by increasing the smoothness boundary
B.
For checking n and ak-1 is divisible by p, k is
selected sufficiently large to ensure p-1 divides k, If the specific type prime
factor is less than กิn, in the worst case, the smoothness boundary B can
be equal to 41.
However, since the composite number n is an unknown, sometimes, the algorithm
may return a false response. For example:
Pollard's P-1 Methed by Smooth Number Example 3
For example: n=533=p*q=13*41; let B=32 imply
| Integer |
B-smooth number |
Prime Factors |
number |
| k |
32 |
25*33*52*71*111*131 * 171*191*231*291*311 =
32*27*25*7*11*13*17 *19*23*29*31 |
144403552893600 |
Therefore for B=32, k32 or (p32-1)m32 is equal to 144403552893600.
Fermat's Little Theorem
let a=2, by Fermat's little theorem,
let p be one of the prime factors of n, imply p divides ak-1.
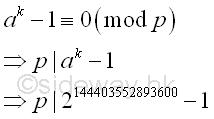
Greatest Common Divisor
Since ak-1 is a very large number, before finding the
greatest common divisor of n and ak-1, ak-1 can be raised to the high power modulo n. Imply
Using squarings modulo
| base |
number; a=2; k=144403552893600; n=533 |
| ak base 10 |
2144403552893600 |
| ai base 10 |
21 = 21 ก
2 (mod 533) |
| 22 = 22 ≡ 4 (mod
533) |
| 24 = 42 ≡ 16 (mod
533) |
| 28 = 162 ≡
256 (mod 533) |
| 216 = 2562 ≡
510 (mod 533) |
| 232 = 5102 ≡
529 (mod 533) |
| 264 = 5292 ≡
16 (mod 533) |
| 2128 = 162 ≡
256 (mod 533) |
| 2256 = 2562 ≡
510 (mod 533) |
| 2512 = 5102 ≡
529 (mod 533) |
| 21024 = 5292 ≡
16 (mod 533) |
| 22048 = 162 ≡
256 (mod 533) |
| 24096 = 2562 ≡
510 (mod 533) |
| 28192 = 5102 ≡
529 (mod 533) |
| 216384 = 5292 ≡
16 (mod 533) |
| 232768 = 162 ≡
256 (mod 533) |
| 265536 = 2562 ≡
510 (mod 533) |
| 2131072 = 5102 ≡
529 (mod 533) |
| 2262144 = 5292 ≡
16 (mod 533) |
| 2524288 = 162 ≡
256 (mod 533) |
| 21048576 = 2562 ≡
510 (mod 533) |
| 22097152 = 5102 ≡
529 (mod 533) |
| 24194304 = 5292 ≡
16 (mod 533) |
| 28388608 = 162 ≡
256 (mod 533) |
| 216777216 = 2562 ≡
510 (mod 533) |
| 233554432 = 5102 ≡
529 (mod 533) |
| 267108864 = 5292 ≡
16 (mod 533) |
| 2134217728 = 162 ≡
256 (mod 533) |
| 2268435456 = 2562 ≡
510 (mod 533) |
| 2536870912 = 5102 ≡
529 (mod 533) |
| 21073741824 = 5292 ≡
16 (mod 533) |
| 22147483648 = 162 ≡
256 (mod 533) |
| 24294967296 = 2562 ≡
510 (mod 533) |
| 28589934592 = 5102 ≡
529 (mod 533) |
| 217179869184 = 5292 ≡
16 (mod 533) |
| 234359738368 = 162 ≡
256 (mod 533) |
| 268719476736 = 2562 ≡
510 (mod 533) |
| 2137438953472 = 5102 ≡
529 (mod 533) |
| 2274877906944 = 5292 ≡
16 (mod 533) |
| 2549755813888 = 162 ≡
256 (mod 533) |
| 21099511627776 = 2562 ≡
510 (mod 533) |
| 22199023255552 = 5102 ≡
529 (mod 533) |
| 24398046511104 = 5292 ≡
16 (mod 533) |
| 28796093022208 = 162 ≡
256 (mod 533) |
| 217592186044416 = 2562 ≡
510 (mod 533) |
| 235184372088832 = 5102 ≡
529 (mod 533) |
| 270368744177664 = 5292 ≡
16 (mod 533) |
| 2140737488355328 = 162 ≡
256 (mod 533) |
| ak base 10 |
2^(140737488355328+ 2199023255552+ 1099511627776+
274877906944+ 68719476736+17179869184+ 4294967296+ 2147483648+ 268435456+
33554432+ 4194304+ 2097152+ 1048576+ 524288+ 65536+ 16384+ 8192+ 4096+ 2048+
512+ 128+ 32) |
| ak base 10 |
2140737488355328*22199023255552*21099511627776*2274877906944* 268719476736*217179869184*24294967296*22147483648*2268435456* 233554432*24194304*22097152*21048576*2524288*
265536*216384*28192*24096*22048*2512*2128*232 |
| ak base 10 |
256*529*510*16*510*16*510*256*510*529*
16*529*510*256*510*16*529*510*256*529*256*529 ≡
1 (mod 533) |
Imply
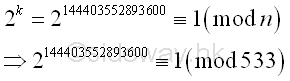
The algorithm returns a fail response, because the number n divides ak-1
and n is the greatest common divisor of n and ak-1.
Imply
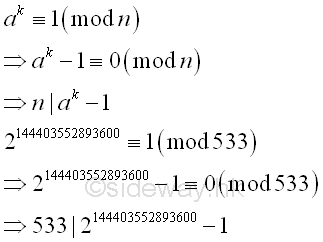
Therefore every prime factor of number n divides ak-1,
imply
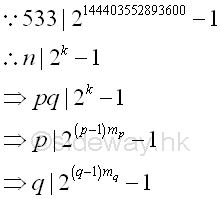
Since the chosen B is much bigger than need,
for this case, which is similar to the case
in smooth number, k is likely to be the common multiple of p-1 and q-1, imply
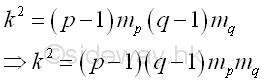
Therefore, one way is to select a smaller B so that k is not the common multiple
of both p-1 and q-1. Let B=4, Imply
| Integer |
B-smooth number |
Prime Factors |
number |
| k |
4 |
22*31
= 4*3 |
12 |
Therefore for B=4, k4 or (p4-1)m4 is equal to 12.
Fermat's Little Theorem
let a=2, by Fermat's little theorem,
let p be one of the prime factors of n, imply p divides ak-1.
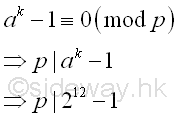
Greatest Common Divisor
Since ak-1 is a very large number, before finding the
greatest common divisor of n and ak-1, ak-1 can be raised to the high power modulo n. Imply
Using squarings modulo
| base |
number; a=2; k=12; n=533 |
| ak base 10 |
212 |
| ai base 10 |
21 = 21 ก
2 (mod 533) |
| 22 = 22 ≡ 4 (mod
533) |
| 24 = 42 ≡ 16 (mod
533) |
| 28 = 162 ≡
256 (mod 533) |
| ak base 10 |
28+4 |
| ak base 10 |
28*24 |
| ak base 10 |
16*256 ≡
365 (mod 533) |
Imply
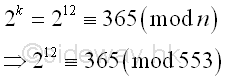
The
greatest common divisor of n and ak-1 is
Using Euclid's algorithm
| ak-1 |
n |
| 212-1 |
533 |
| 365-1 |
533 |
| 364 |
533-364=169 |
| 364-2*169=26 |
169 |
| 26 |
169-6*26=13 |
| 26-2*13=0 |
13 |
| 0 |
13 |
Imply
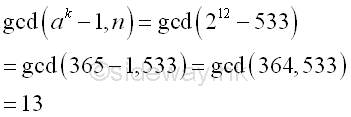
Integer 13, the
greatest common divisor of n and ak-1 is also the
prime divisor of n. And p-1 is 4-powersmooth.
| Integer |
B-smooth number |
Prime Factors |
number |
| p-1 |
4 |
22*31 |
12 |
| k |
4 |
22*31
= 4*3 |
12 |
| k/(p-1) |
|
20*30 |
1 |
Besides, for B=32
| Integer |
B-smooth number |
Prime Factors |
number |
| p-1 |
4 |
22*31 |
12 |
| q-1 |
8 |
23*30*51*70 |
40 |
| k |
32 |
25*33*52*71*111*131*171*191 231*291*311 |
144403552893600 |
| k/(p-1)(q-1) |
|
20*32*51*71*111*131*171*191
231*291*311 |
300840735195 |
Link:http://output.to/sideway/default.asp?qno=120500010 Pollard's p-1 Method
Pollard's p-1 Method
Pollard's p-1 method is a prime factorization algorithm
discovered by John Pollard
in 1974. Limited by the algorithm, the Pollard's p-1 method is only work for
integers with specific factors.
If the number n has a prime factor p such that p-1 can be expressed in terms of
a product of primes, the finding of prime factor p is based on the selected
boundary B of the B-powersmooth number. The algorithm fails when the selected
boundary B is smaller than the B-powersmooth number of p-1.
Pollard's P-1 Methed by
PowerSmooth Number
Pollard's P-1 Methed by
PowerSmooth Number Example 2
For example: n=667=p*q=23*29; let B=5 imply
| Integer |
B-smooth number |
Prime Factors |
number |
| k |
5 |
22*31*51 = 4*3*5 |
60 |
Therefore for B=5, k5 or (p5-1)m5 is equal to 60.
Fermat's Little Theorem
let a=2, by Fermat's little theorem,
let p be one of the prime factors of n, imply p idivides ak-1.
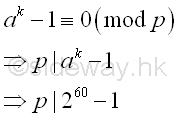
Greatest Common Divisor
Since ak-1 is a very large number, before finding the
greatest common divisor of n and ak-1, ak-1 can be raised to the high power modulo n. Imply
Using squarings modulo
| base |
number; a=2; k=60; n=667 |
| ak base 10 |
260 |
| ai base 10 |
21 = 21 ≡
2 (mod 667) |
| 22 = 22 ≡ 4 (mod
667) |
| 24 = 42 ≡ 16 (mod
667) |
| 28 = 162 ≡
256 (mod 667) |
| 216 = 2562 ≡
170 (mod 667) |
| 232 = 1702 ≡
219 (mod 667) |
| ak base 10 |
232+16+8+4 |
| ak base 10 |
232*216*28*24 |
| ak base 10 |
219*170*256*16 ≡
538 (mod 667) |
and using
the residue to calculate the greatest common divisor. Imply
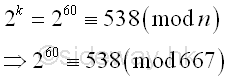
The
greatest common divisor of n and ak-1 is
Using Euclid's algorithm
| ak-1 |
n |
| 260-1 |
667 |
| 538-1 |
667 |
| 537 |
667-537=130 |
| 537-4*130=17 |
130 |
| 17 |
130-7*17=11 |
| 17-11=6 |
11 |
| 6 |
11-6=5 |
| 6-5=1 |
5 |
| 1 |
5-5*1=0 |
| 1 |
0 |
Imply
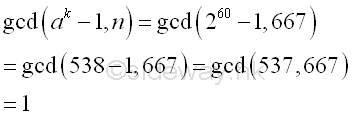
The
algorithm fails because the greatest common divisor of n and ak-1
is equal to 1. The number n does not have
prime divisor p with p-1 is 5-powersmooth. Therefore the bound B equals to 5 fails, a
larger bound B' should be used.
Let B=7, imply
| Integer |
B-powersmooth number |
Prime Factors |
number |
| k |
7 |
22*31*51*71
= 4*3*5*7 |
60 * 7 = 420 |
Therefore for B=7, k7 or (p7-1)m7 is equal to 60*7 = 420. Imply k7
= k5 * 7. And the new ak
can be expressed as
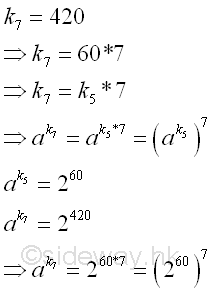
And ak can be raised to the high power modulo n, imply
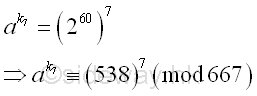
Using squarings modulo
| base |
number; a=538; k=7*; n=667 |
| ak base 10 |
5387 (mod 667) |
| ai base 10 |
5381 = 5381 ≡
538 (mod 667) |
| 5382 = 5382 ≡
633 (mod 667) |
| 5384 = 6332 ≡
489 (mod
667) |
| ak base 10 |
5384+2+1 (mod 667) |
| ak base 10 |
5384*5382*5381 (mod 667) |
| ak base 10 |
489*633*538 ≡ 349 (mod 667) |
and using
the residue to calculate the greatest common divisor. Imply
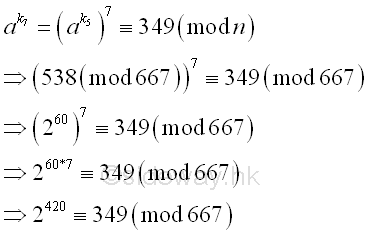
The
greatest common divisor of n and ak-1 is
Using Euclid's algorithm
| ak-1 |
n |
| 2420-1 |
667 |
| 349-1 |
667 |
| 348 |
667-348=319 |
| 348-319=29 |
319 |
| 29 |
319-11*29=0 |
| 29 |
0 |
Imply
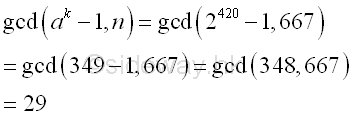
Integer 29, the
greatest common divisor of n and ak-1 is also the
prime divisor of n. And p-1 is 7-powersmooth.
| Integer |
B-powersmooth number |
Prime Factors |
number |
| p-1 |
7 |
22*71 |
28 |
| k |
7 |
22*31*51*71
= 4*3*5*7 |
420 |
| k/(p-1) |
|
20*31*51*70 |
15 |
Link:http://output.to/sideway/default.asp?qno=120500009 Pollard's p-1 Method
Pollard's p-1 Method
Pollard's p-1 method is a prime factorization algorithm
discovered by John Pollard
in 1974. Limited by the algorithm, the Pollard's p-1 method is only work for
integers with specific factors.
One issue of the Pollard's p-1 method by smooth number is the value of k is
usually much larger than needed in order to ensure p-1 divides k. Therefore
alternative selection of k are developed to reduce the time of computation.
Alternative methods of selection of k are
-
limit the index or power ei for each prime factor pi such that the prime power is just less than and equal
to กิn.
-
let k equal to B!
-
let k equal to the least common multiple of 1,2,3,...B
Although these methods can reduce the value of k, there is also the possibility
that the prime factor p with p-1 is B-smooth of a number n is excluded such that
p-1 does not divide k.
PowerSmooth Number Method
PowerSmooth Number
Another number choosing method for integer k is the making use of the concept of
powersmooth number and the specific type of prime factor, i.e. p-1 is the
product of primes.
Let x and B be integers. x is said to be B-powersmooth if all the prime power
for dividing n are less than or equal to B.
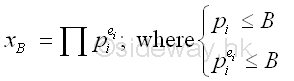
Example of
PowerSmooth Number
| B |
B-powersmooth numbers |
Prime Factors |
| 2,3,4,5,6,7,8,9,10,11,... |
1 |
20,30,50,70,110,... |
| 2,3,4,5,6,7,8,9,10,11,... |
2 |
21, |
| 3,4,5,6,7,8,9,10,11,... |
3 |
31, |
| 4,5,6,7,8,9,10,11,... |
4 |
22, |
| 5,6,7,8,9,10,11,... |
5 |
51, |
| 3,4,5,6,7,8,9,10,11,... |
6 |
21,31, |
| 7,8,9,10,11,... |
7 |
71, |
| 8,9,10,11,... |
8 |
23, |
| 9,10,11,... |
9 |
32, |
| 5,6,7,8,9,10,11,... |
10 |
21,51, |
| 11,... |
11 |
111, |
Unlike smooth number, B is usually considered as the maximum boundry of a group
of number. Therefore B can be prime number or composite number providing that
B is greater than or equal to the largest prime power factor of x. The key
information from a B-powersmooth number is the prime power factor of a number.
The lowest B-powersmooth of a number is larger than or equal to the greatest prime
power factor of the number.
Unlike B-smooth number, B-powersmooth number represents a finite set of numbers.
Imply
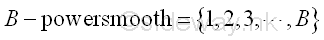
Therefore, x can be defined as the least common multiple of the numbers from 1
to B.
Imply
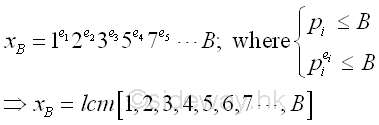
Pollard's P-1 Methed by PowerSmooth Number
Since p-1 divides k, by assuming p-1 is B-powersmooth, if k is also
B-powersmooth then the choosen integer k should be sufficienly large to ensure
p-1 divides k. Therefore k is equal to the least common multiple of
all numbers less than and equal to B. Imply
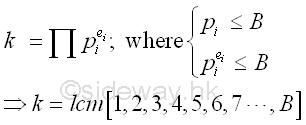
Let k equal to xB. Assume p-1 is B-powersmooth, then
p-1 divides k.
Pollard's P-1 Method by
PowerSmooth Number Example 1
For example: n=203=p*q=7*29; let B=5 imply
| Integern">Integer |
B-powersmooth number |
Prime Factors |
number |
| k |
5 |
22*31*51 = 4*3*5 |
60 |
Therefore for B=5, kfor B=5, k5 or (p5-1)m5 is equal to 60.
Fermat's Little Theorem
let a=2, by Fermat's little theorem,
let p be one of the prime factors of n, imply p divides ak-1.
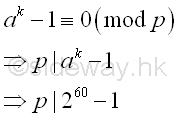
Greatest Common Divisor
Since ak-1 is a very large number, before finding the
greatest common divisor of n and ak-1, ak-1 can be raised to the high power modulo n. Imply
Using squarings modulo
| base |
number; a=2; k=60; n=203 |
| ak base 10 |
260 |
| ai base 10 |
21 = 21 ก
2 (mod 203) |
| 22 = 22 ≡ 4 (mod
203) |
| 24 = 42 ≡ 16 (mod
203) |
| 28 = 162 ≡
53 (mod 203) |
| 216 = 532 ≡
170 (mod 203) |
| 232 = 1702 ≡
74 (mod 203) |
| ak base 10 |
232+16+8+4 |
| ak base 10 |
232*216*28*24 |
| ak base 10 |
74*170*53*16 ≡
190 (mod 203) |
Imply
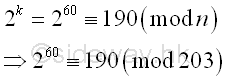
The
greatest common divisor of n and ak-1 is
Using Euclid's algorithm
| ak-1 |
n |
| 260-1 |
203 |
| 190-1 |
203 |
| 189 |
203 |
| 189 |
203-189 |
| 189 |
7 |
| 189-27*7 |
7 |
| 0 |
7 |
Imply
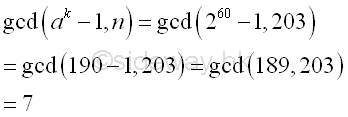
Integer 7, the
greatest common divisor of n and ak-1 is also the
prime divisor of n. And p-1 is 5-powersmooth.
| Integer |
B-powersmooth number |
Prime Factors |
number |
| p-1 |
3, 5 |
21*31 |
6 |
| k |
5 |
22*31*51
= 4*3*5 |
60 |
| k/(p-1) |
|
21*30*51 |
10 |
Since the greatest prime
power factor of p-1 is 3-smooth also. And therefore the prime
factor 7 can also be found by using B=3
| Integer |
B-powersmooth number |
Prime Factors |
number |
| p-1 |
3 |
21*31 |
6 |
| k |
3 |
21*31
= 2*3 |
6 |
| k/(p-1) |
|
20*30 |
1 |
let a=2, by Fermat's little theorem, imply p divides
26-1 ≡ 63 (mod 203)
The
greatest common divisor of n and ak-1 is gcd(63,203)=
7
And 7 is the prime divisor of n as before.
|
|
 Sideway
BICK BLOG from Sideway
Sideway
BICK BLOG from Sideway