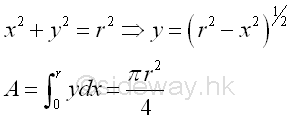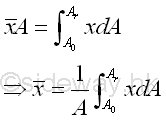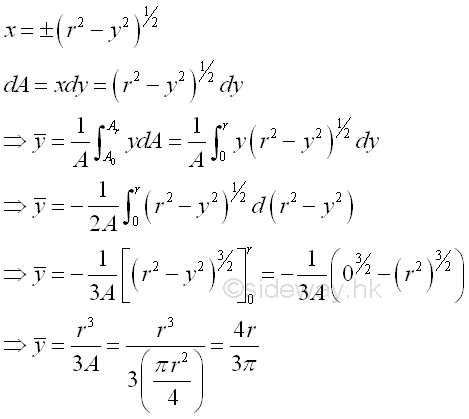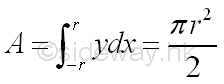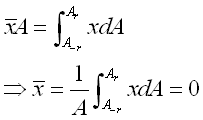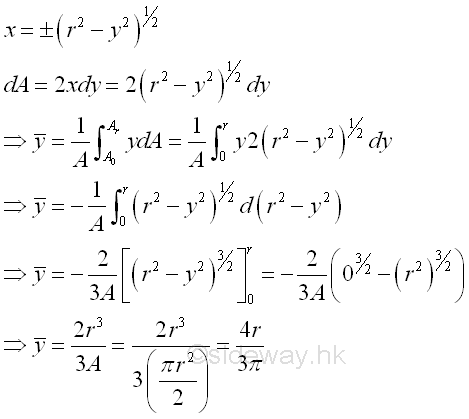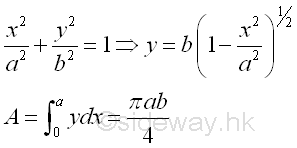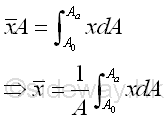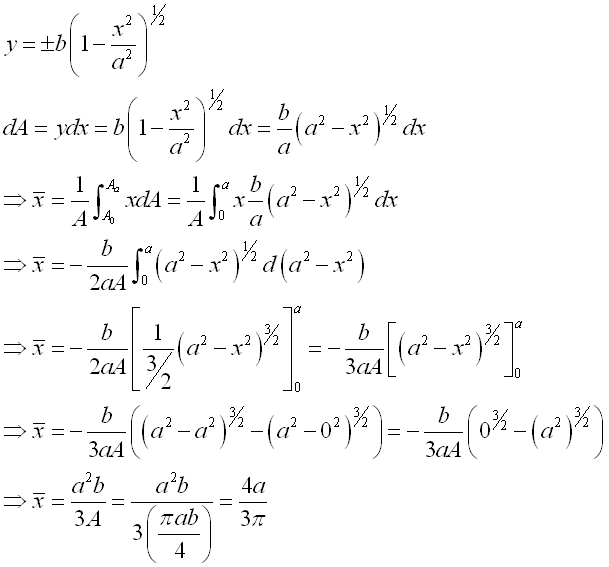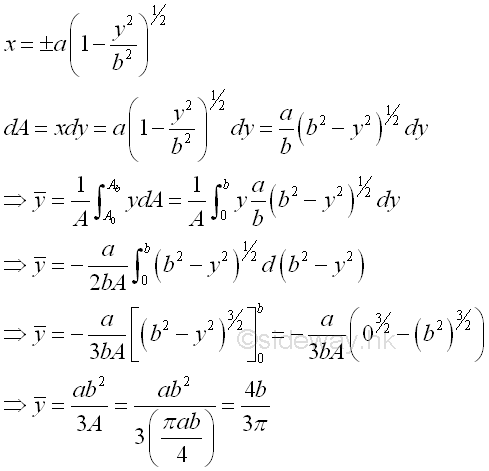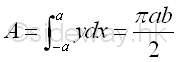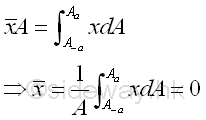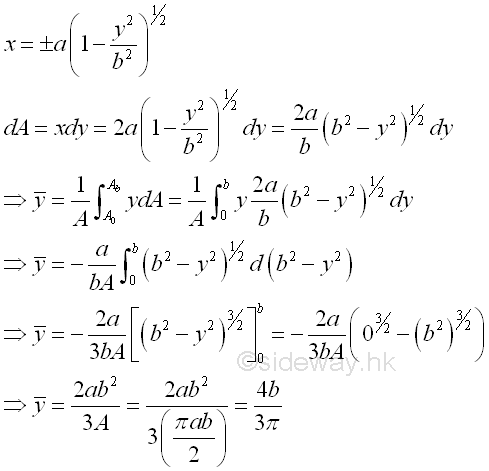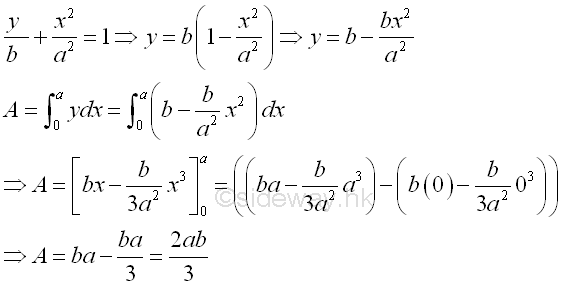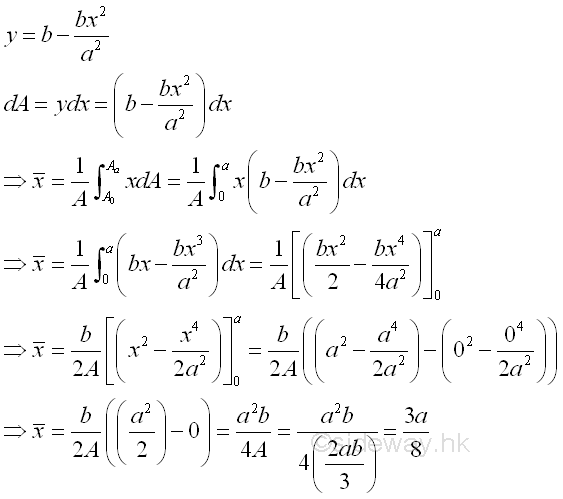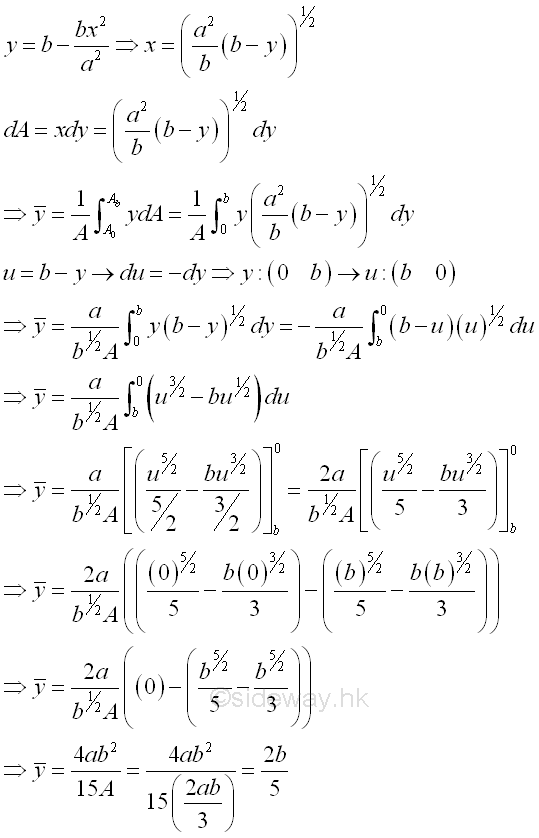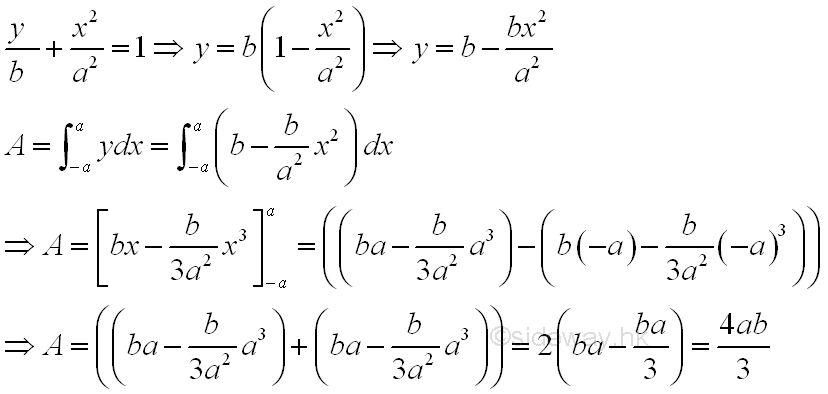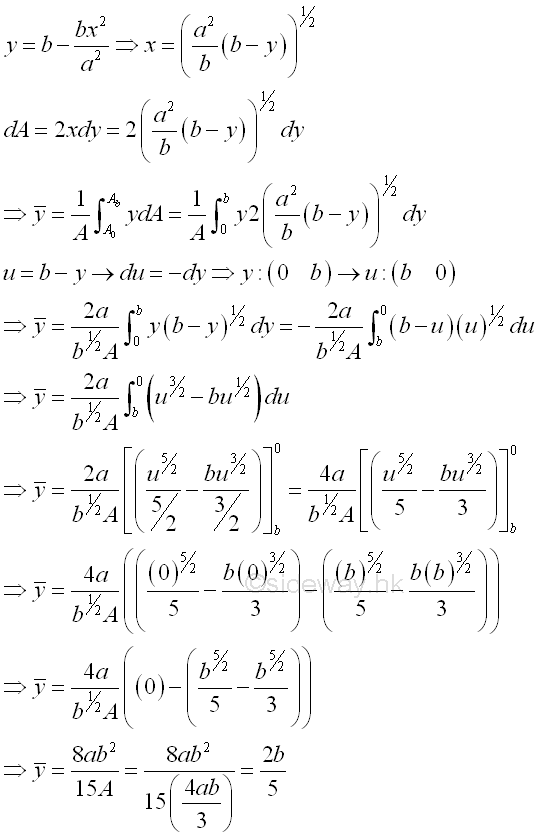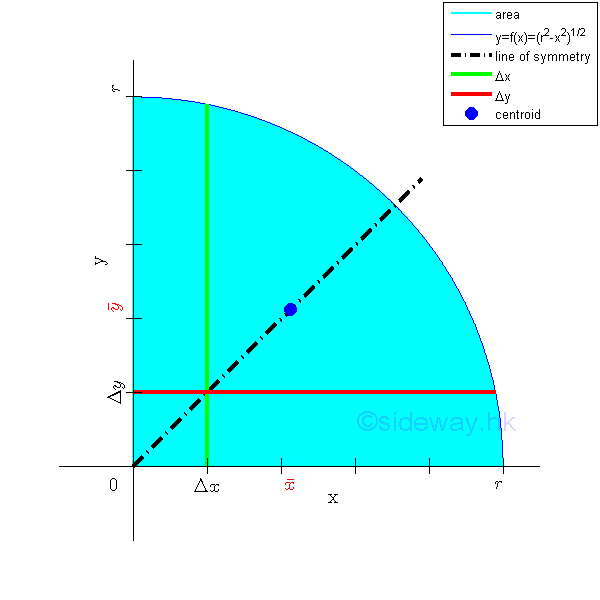
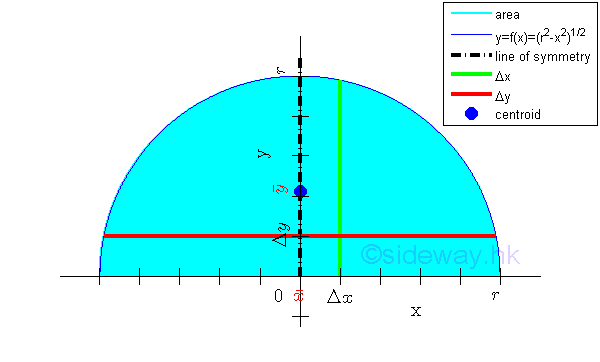
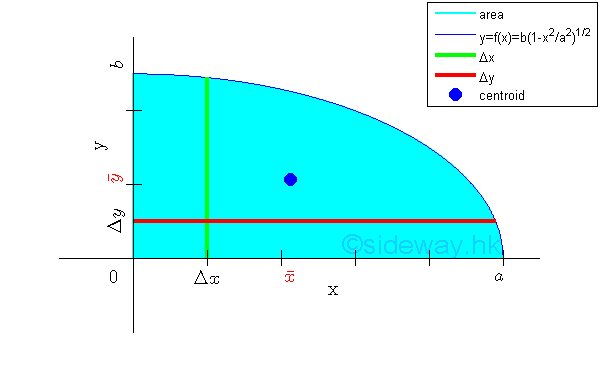
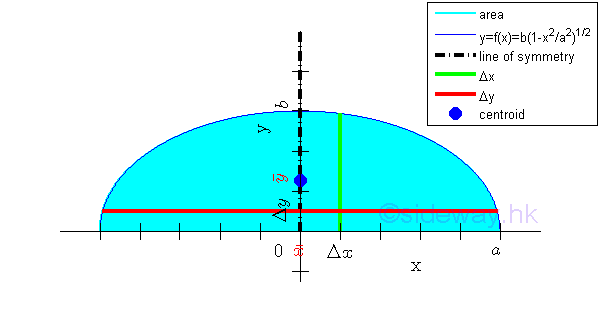
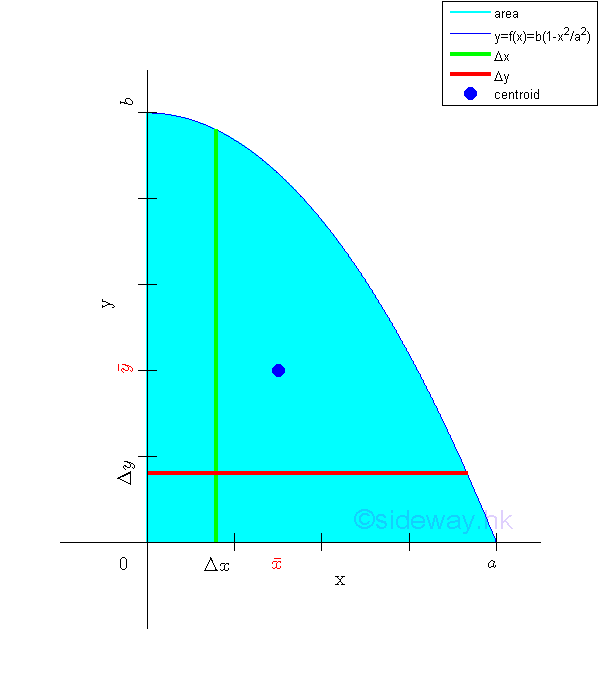
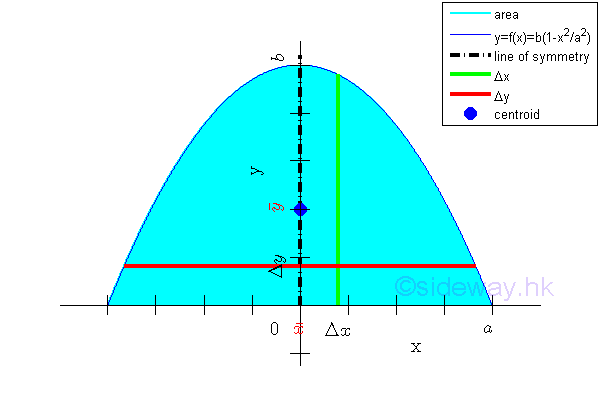
Centroid of 2D Plane Body

The centroid of an plate is determined by the first moment of a two dimensional plane body with the method of the first moment of area.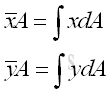

And the centroid of a wire is determined by the first moment of a two dimensional plane body with the method of the first moment of line.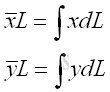

Centroids of Shapes

1. Centroid of Quarter-Circular Area

   Area of Quarter-Circular: http://output.to/sideway/default.asp?qno=111100013

   

   Coordinate x of centroid by integration.

   

   Coordinate x of centroid

   

   Similarly, coordinate y of centroid by integration.

   
2. Centroid of Semi-Circular Area

   Area of Semi-Circular: http://output.to/sideway/default.asp?qno=111100013

   

   Coordinate x of centroid by symmetry.

   

   Coordinate y of centroid by integration.

   
3. Centroid of Quarter-Elliptical Area

   Area of Quarter-Elliptical: http://output.to/sideway/default.asp?qno=111100013

   

   Coordinate x of centroid by integration.

   

   Coordinate x of centroid by integration.

   

   Similarly, coordinate y of centroid by integration.

   
4. Centroid of Semi-Elliptical Area

   Area of Semi-Elliptical: http://output.to/sideway/default.asp?qno=111100013

   

   Coordinate x of centroid by symmetry.

   

   Coordinate y of centroid by integration.

   
5. Centroid of Quarter-Parabolic Area

   Area of Quarter-Parabolic:

   

   Coordinate x of centroid by integration.

   

   Coordinate x of centroid by integration.

   

   Similarly, coordinate y of centroid by integration.

   
6. Centroid of Quarter-Parabolic Area

   Area of Quarter-Parabolic:

   

   Coordinate x of centroid by symmetry.

   

   Similarly, coordinate y of centroid by integration.

   

Pollard's p-1 Method

Pollard's p-1 method is a prime factorization algorithm discovered by John Pollard in 1974. Limited by the algorithm, the Pollard's p-1 method is only work for integers with specific factors.

However, since the composite number n is an unknown, sometimes, the algorithm may return a false response. Besides caused by finding all prime factors simulatanously due to a large B, the Polloard's p-1 method will also fail because of the pseudoprime like property.

Characteristic of Pollard's p-1 Method by PowerSmooth Number

The advantage of Pollard's p-1 method by powersmooth number is the checking of a group of  primes with one computation. Every boundary B represents a group of numbers that can be expressed as the product of prime power factors less than and equal to number B.

However, since the composite number n is an unknown, sometimes, the algorithm may return a false response. For example: 

Pollard's P-1 Methed by Smooth Number Example 4

For example: n=533=p*q=13*41; let B=5 imply

Integer	B-smooth number	Prime Factors	number
k	5	22*31*51 = 4*3*5	60

Therefore for B=5, k5 or (p5-1)m5 is equal to 60.

Fermat's Little Theorem

let a=2, by Fermat's little theorem, let p be one of the prime factors of n, imply p divides ak-1.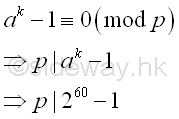

Greatest Common Divisor

Since ak-1 is a very large number, before finding the greatest common divisor of n and ak-1,  ak-1 can be raised to the high power modulo n. Imply

Using squarings modulo

base	number; a=2; k=60; n=533
ak base 10	260
ai base 10	21  = 21 ≡ 2 (mod 533)
	22 = 22 ≡ 4 (mod 533)
	24 = 42 ≡ 16 (mod 533)
	28 = 162 ≡ 256 (mod 533)
	216 = 2562 ≡ 510 (mod 533)
	232 = 5102 ≡ 529 (mod 533)
ak base 10	232+16+8+4
ak base 10	232*216*28*24
ak base 10	529*510*256*16 ≡ 1 (mod 533)

Imply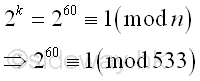 

The algorithm returns a fail response, because the number n divides ak-1 and n is the greatest common divisor of n and ak-1. Imply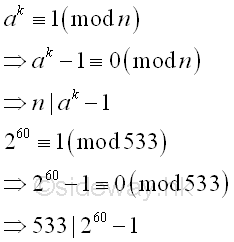

Therefore every prime factor of number n divides ak-1, imply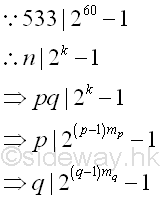

For this case, since k is not large enough to be the common multiple of p-1 and q-1, imply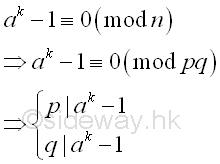

Therefore, one way is to select another a so that ak-1 is not the common multiple of both p and q. Let a=3, and B=5 Imply

Integer	B-smooth number	Prime Factors	number
k	5	22*31*51 = 4*3*5	60

Therefore for B=5, k5 or (p5-1)m5 is equal to 60.

Fermat's Little Theorem

let a=3, by Fermat's little theorem, let p be one of the prime factors of n, imply p divides ak-1.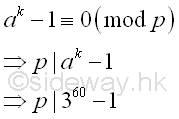

Greatest Common Divisor

Since ak-1 is a very large number, before finding the greatest common divisor of n and ak-1,  ak-1 can be raised to the high power modulo n. Imply

Using squarings modulo

base	number; a=3; k=60; n=533
ak base 10	360
ai base 10	31  = 31 ≡ 3 (mod 533)
	32 = 32 ≡ 9 (mod 533)
	34 = 92 ≡ 81 (mod 533)
	38 = 812 ≡ 165 (mod 533)
	316 = 1652 ≡ 42 (mod 533)
	332 = 422 ≡ 165 (mod 533)
ak base 10	332+16+8+4
ak base 10	332*316*38*34
ak base 10	165*42*165*81 ≡ 40 (mod 533)

Imply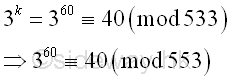 

The greatest common divisor of n and ak-1 is

Using Euclid's algorithm

ak-1	n
360-1	533
40-1	533
39	533-13*39=26
39-26=13	26
13	26-2*13=0
13	0

Imply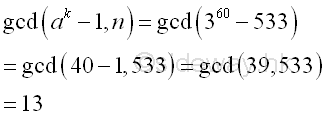

Integer 13, the greatest common divisor of n and ak-1 is also the prime divisor of n. And p-1 is  5-smooth. For a=2

Integer	B-smooth number	Prime Factors	number
p-1	4,5	22*31	12
q-1	5	23*51	40
k5	5	22*31*51 = 4*3*5	60
k5/(p-1)		20*30*51	5
k5/(p-1)(q-1)		20*30*50/23*30*50	1/8

Besides, for B=5; a=2 and a=3

Integer	Prime Factors	number
p	13	13
q	41	41
n	13*41	533
2k-1	32*52*71*111*131*311* 411*611*1511*3311*13211	1152921504606846975
3k-1	24*52*71*112*131*311*611*731* 2711*11811*45611*477633611	42391158275216203514294433200
(2k-1)/pq	32*52*71*111*131*310* 410*611*1511*3311*13211	2163079745979075
(3k-1)/pq	24*52*71*112*130*311*611*731* 2711*11811*45611*477633611	3260858328862784885714956400 /41