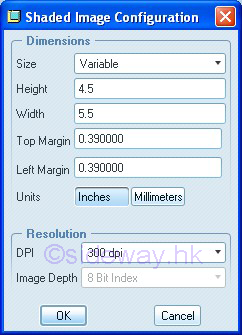
Save file as Image

 "File" -"Save a Copy"-"Type" can be used to export the image in the working window to an image file. The two important setting of the image is the output dimension and the resolution. In general, a suitable dimension is size choosing variable with height equal to 4.5 in and width equal to 5.5 in and the acceptable resolution is 300 dpi.

For example, the shaded image configuration of a jpeg image

 

Equilibrium Equations in Three Dimensions

The number of unknown for a reaction to represent the support and connection is equal to 1 to 6 depending on the type of support and connection. Since maximum six unknowns can be determined in the three dimensional rigid structure. In general, unknown forces of equilibrium rigid body with simple support and connection in three dimensions can be determined by the application of equilibrium equations.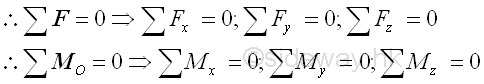

However, unlike the case in two dimensions, three dimensional problems are much more difficult because the involving of setting up and solving six indepentent equilibrium equations simultaneously

Alternative Forms of Equilibrium Equations

As in two dimensions, when a rigid body in three dimensional space is in static equilibrium state, the moment at any point or any axis in the structure is equal to zero also. It is quite difficult to set up the equilibrium equations directly.

In three dimensioal space, the convenient way to determine the unknowns is using vector operations by expressing the force and position vectors in terms of unit vectors after selecting a point O and defining the coordinate axis system, imply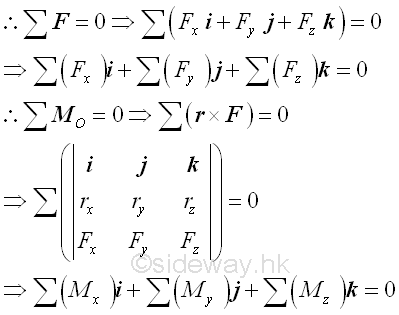

The six scalar equilibrium equations can then be obtained by equating the coefficients of the unit vector of the equilibrium force equation and equilibrium moment equation to zero.

Since there are only three force equilibrium equations in space, and the structure may have totally maximum six unknowns in the force equilibrium equations, the three unknowns out of the six should be determined by equilibrium moment equation. Therefore, the choice of the taking moment point or axis should have maximum three unknowns. 

Besides, sometimes it is also useful to consider taking moment about an axis to determine an unknown or the relationship between unknowns, imply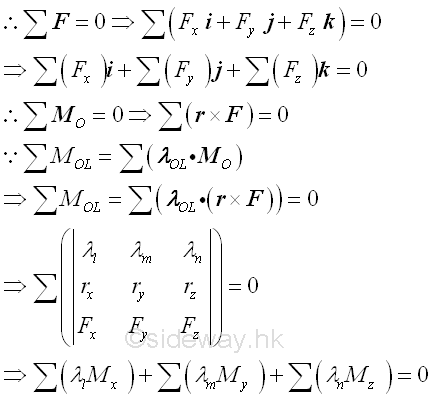

Two more independent equations can be obtained by using two other reference axes.

Mechanical Constraints of Structure

If the provided reactions are more than necessary for holding the structure in space, more than six unknowns will be involved. Since more unknowns than the indepentent equilibrium equations, some of the reactions will be statically indeterminate.

If the provided reactions for holding the structure in space involve less than six unknown, some of the indepentent equilibrium equations will not be satisfied under all given loads or any other loading conditions acting on it. The structure is therefore only partially constrained.

However, in many practical engineering problems, under a particular loading conditions or a specific working condition, the unsatisifed equilibrium equations usually can be reduced to a trival solution. And the related reactions can be disregrarded and be ignored in the specified working condition.

In general, a properly contrained structure in space should have three rectangular translational constraints and three rectangular rotational constraints. But in some case, although the structure may have the correct number or more of unknowns provided by support and connection, the six independent equation still can not be satisified if the structure is improperly constrained. For example, translational constraint will be repeated by supports with parallel lines of action, or  rotational constraint will be destroyed when supports with intersecting lines of action.