Sideway
BICK BLOG from Sideway
Sideway
BICK BLOG from Sideway
|
Link:http://output.to/sideway/default.asp?qno=120200061 Equilibrium in Two Dimensions Equilibrium in Two DimensionsMany practical engineering problem can be considered as a planar rigid body in two dimensions. The conditions for the equilibrium of a rigid body is.
By neglecting the z axis dimension. Imply 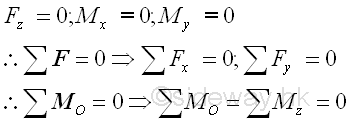
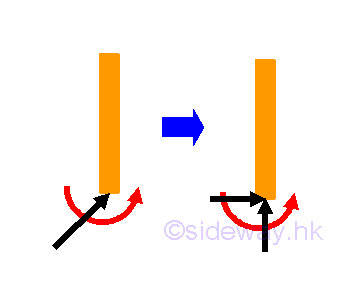
When a rigid body is in static equilibrium state, the moment at any point A in the planar structure is equal to zero also, imply 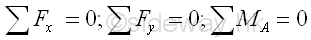
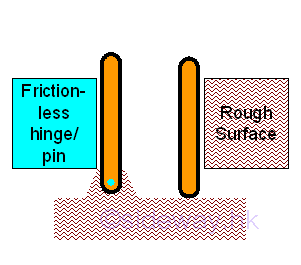
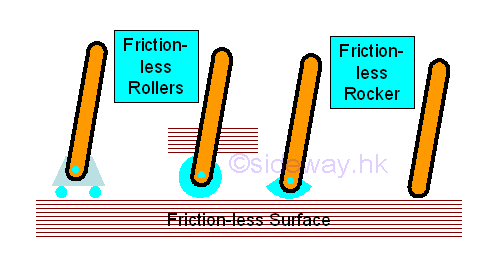
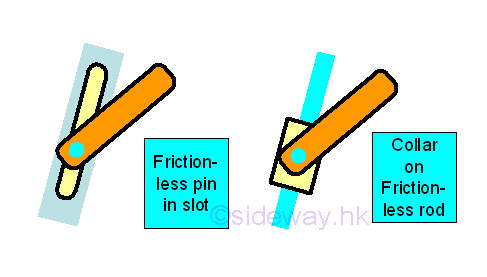
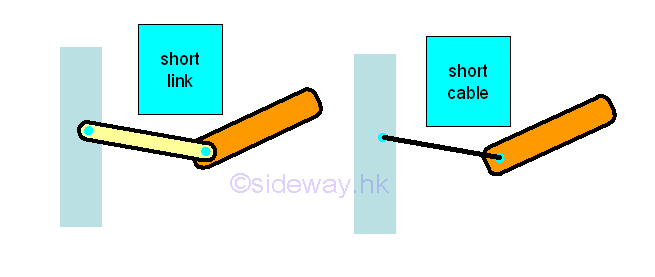
Only two translational and one rotational motion are needed for determining a two dimensional structure is in static equilibrium state or not. In other words, the possible forces and moments due to an applied action or a reaction in a two dimensional structure are two rectangular forces and one moment, or one resultant force and one moment. Since there are only three equations obtained from the equilibrium equations of a rigid body in two dimenstion, no more than three unknowns can be determined by the system of three equations. Reactions at Supports and ConnectionsIn order to construct the free body diagram for analysing the equilibrium of rigid body in two dimensions, the types of reactions at supports and connections should be evaluated first. The types of reactions at supports and connections can be divided into three types:
Link:http://output.to/sideway/default.asp?qno=120200062 Equilibrium in Two Dimensions Equilibrium Equations in Two DimensionsThe number of unknown for a reaction to represent the support and connection is equal to 1 to 3 depending on the type of support and connection. Since maximum three unknowns can be determined in the two dimensional rigid structure, in general, unknown forces of an equilibrium rigid body with simple support and connection in two dimensions can be determined by the application of equilibrium equations. 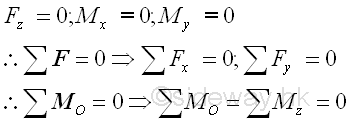
For example, a structure of mass, m, is fixed by a hinge pin at one of its lower end and support by a roller at the other lower end. 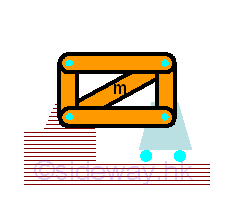
According to the types of support and connection, the free body diagram of the structure is. 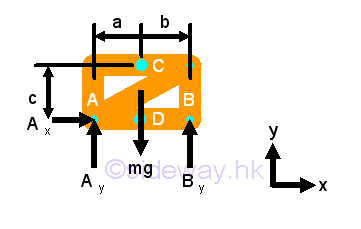
By the equalibrium equations. 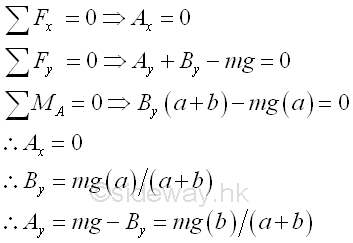
Alternative Forms of Equilibrium EquationsSince when a rigid body is in static equilibrium state, the moment at any point in the planar structure is equal to zero also, imply the moment at point B is equal to zero also. Imply 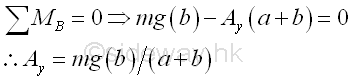
This additional equation is not an independent equation, no new information can be obtained from this equation, and the additional equation can not be used to determine a fourth unknown. However, by taking moment at B instead of force summation along y direction, the unknown reaction By is reduced. The alternative system of equailibrium equation is 
Similary, the force summation along x direction can also be replaced by taking moment at point, C, such that force Ax is expressed in terms of forces Ay and By. Imply 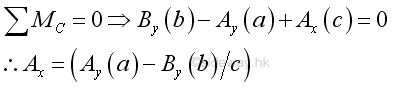
Since the moment at point C can replace the force along x direction, the alternative system of equailibrium equation is 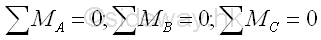
Physically, a rigid body in two dimensions is in equilibrium state, when the force summation in both direction is equivalent to zero and the net moments of all forces are balanced at any point and is equal to zero. Therefore the above two alternative equilibrium equations can be used to simplify the calculation work. However, when considering the moment at point D, imply 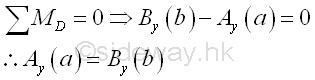
This is only an alternative form of MA or MB, Therefore the selection of moment taking point should be aimed at obtaining equilibrium equation with less unknown variables. Besides these alternative equations can also be used for checking the solution obtained from the origianal or other alternative equilibrium equations. |
Sideway BICK Blog 16/02 |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
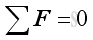 and
and