 Sideway
BICK BLOG from Sideway
Sideway
BICK BLOG from Sideway
|
Link:http://output.to/sideway/default.asp?qno=111000005 Related Motion Related RatesFor motion system with fixed relationship between its input and output, the derivatives, instantaneous rates of change can also be used as related rates of change for determining the unknown rate of change by the known rate of change. Related MotionThe most common related motions are the physical related motions in a mechanical system. Sometimes the related motion can also be other physical systems, for example optical projection. Related Linear Motion - Falling Ladder ProblemA 25 long ladder is leaning against a wall. When the bottom of ladder is moved outward at x=3 with constant speed Vx=3, the top of ladder is being moved downward simultaneously. Since the ladder is rigid and fixed in length, the instantaneous vertical velocity Vy at time 7 is:
According to the given information. The unknown rate of change is the linear displacement along y direction with respect to time t and the known rate of change is the linear displacement along x direction with respect to time t. Both x and y are the Cartesian coordinates. The relationship between x and y in Cartesian coordinates can be related by the length of the ladder through the Pythagorean theorem, i.e. L2=x2+y2. Therefore the mathematical model of the falling ladder is: 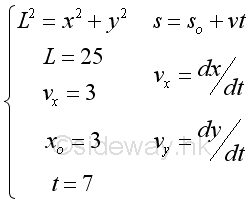
The relationship of the two cartesian instantaneous velocity vx and vy are: 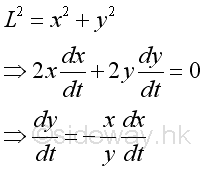
Therefore the instantaneous velocity vy is a function of x and y. And y can be expressed as: 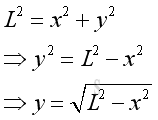
And the position of the bottom of ladder at time t is: 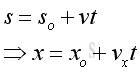
Subsitute all variables and get: 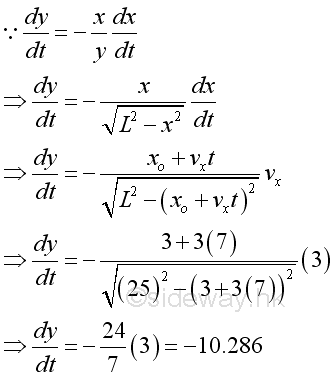
Graphically: 
Intantaneous velocities plot against time: 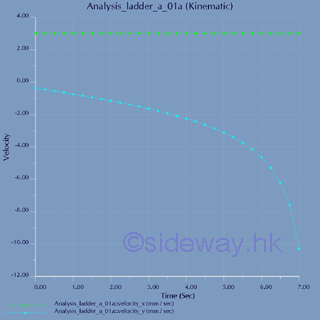
Related Linear Motion - Moving Rod ProblemA guided rod is moving along the x and y axis with fixed enclosed area A=36. When the guided rod is moved outward along x-axis at x=3 with constant speed Vx=3, the guided rod is being moved downward simultaneously. Since the guided rod is rigid and the enclosed area is fixed, the instantaneous vertical velocity Vy along y-axis at time 7 is: 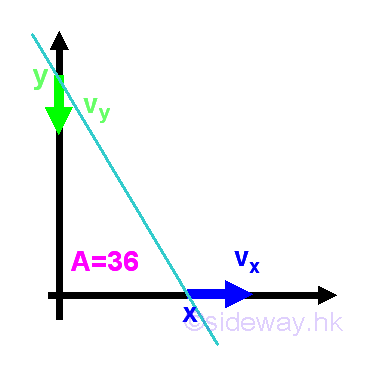
According to the given information. The unknown rate of change is the linear displacement along y direction with respect to time t and the known rate of change is the linear displacement along x direction with respect to time t. Both x and y are the Cartesian coordinates. The relationship between x and y in Cartesian coordinates can be related by the enclosed area, i.e. A=xy/2. Therefore the mathematical model of the falling ladder is: 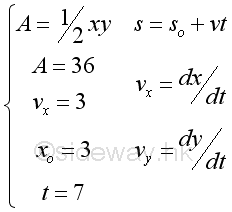
The relationship of the two cartesian instantaneous velocity vx and vy are: 
And the position of the bottom of ladder at time t is: 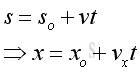
Subsitute all variables and get: 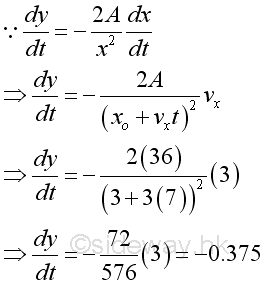
Graphically: 
Intantaneous velocities and displacements plot against time: 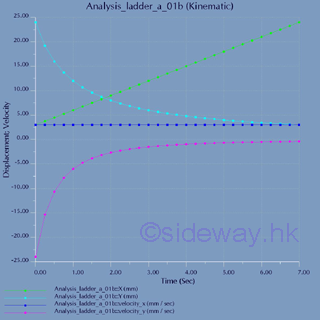
Link:http://output.to/sideway/default.asp?qno=111000006 Related Flow Related RatesFor flowing system, when the relationship between its input and output can be modelled by a function, the derivatives, instantaneous rates of change can also be used as related rates of change for determining the unknown rate of change by the known rate of change. Related flowThe most common related flows are the filling and discharge processes associated with physical system. Sometimes the related flow can also be other physical systems, for example wave propagation. Related Filling Flow ProblemAn inverted conical tank of height H=25 and base radius R=7 are used to collect a flow. When the flow flows into the tank at a constant rate of Q=150, the level of filling is increased simultaneously and the instantaneous rate of level rising, dh/dt at time 7 is:
According to the given information. The unknown rate of change is the vertical level with respect to time t and the known rate of change is the flow volume into the concial tank with respect to time t. Since the shape of conical tank is fixed, the relationship between the height h and radius r is at a fixed ratio. Besides the total volume of flow inside the concial tank can also be determined. Therefore the mathematical model of the filling tank is: 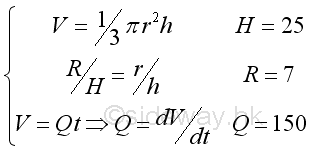
Since r and h are related at a fixed ratio, and both r and h are function of time, r can be expressed in terms of h, imply, 
The relationship between the unknown rate of change and known rate of change can be determined by: 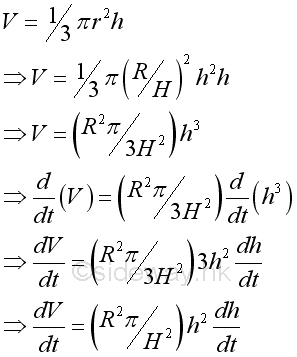
For a constant flow rate, total volume flow at level h can also be expressed in term of time t: 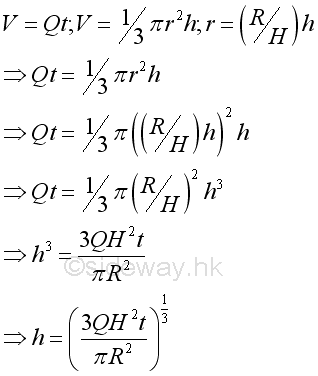
Therefore the relationship between the unknown rate of change and known rate of change in terms of time t is: 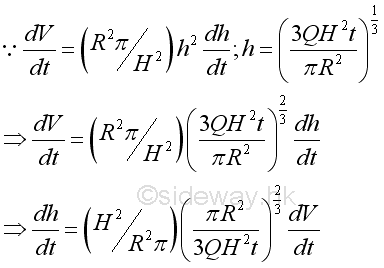
Subsitute all variables and get:
Graphically: 
Intantaneous velocity_level and level plot against time: 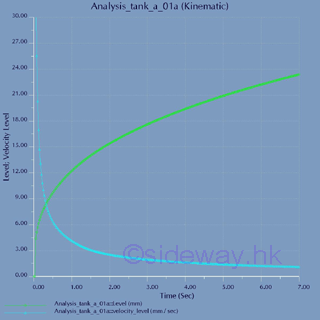
Related Discharge flow ProblemAn inverted conical tank of original height H=25 and base radius R=7 are used as a flow storage. A circular hole of radius ro=1 has been cut off at its apex for draining. The initial level above the hole is ho=20. Liquid drains at a discharge velocity v=√(2gh) for draining. When liquid drains out from the tank, the head or level about the draining hole is decreased simultaneously and the instantaneous rate of level lowering, dh/dt at head h=7 is: 
According to the given information. The unknown rate of change is the vertical level with respect to time t and the known rate of change is the flow velocity drains out from the concial tank as a function of time t. Since the shape of conical tank and the ipex draining opening is fixed, the relationship between the height h and radius r is at a fixed ratio and the driaining volume flow rate is constrained also. Besides the total remaining volume of liquid inside the concial tank can also be determined. Therefore the mathematical model of the tank draining is: 
Since the shape of conical tank is fixed, the relationship between radius r and level h is: 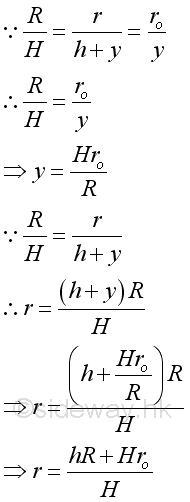
The volume of remaining liquid can also be expressed in terms of level h: 
Therefore the related rates of change between volume and level with respect to time t is: 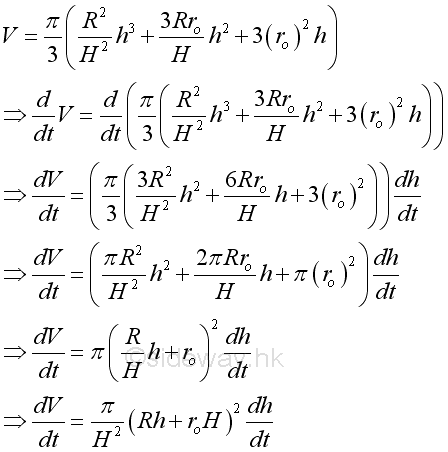
From the given draining velocity, the related rates of change between level and velocity with respect to time t where negative means flow downward is: 
Since the draining opening is fixed, although the draining velocity is not a linear function, the relationship between discharged volume and draining velocity is fixed also. Therefore through infinitesimal approach, the infinitesimal discharged volume with respect to time t is equal to the flow rate that is the flow velocity time the passing through cross-section area. imply: 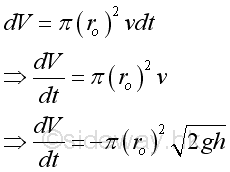
Subsitute all variables and get: 
Graphically: 
Intantaneous velocity_level and level plot against time: 
Link:http://output.to/sideway/default.asp?qno=111000008 linear Collection of linear Motion
|
Sideway BICK Blog 10/10 |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||

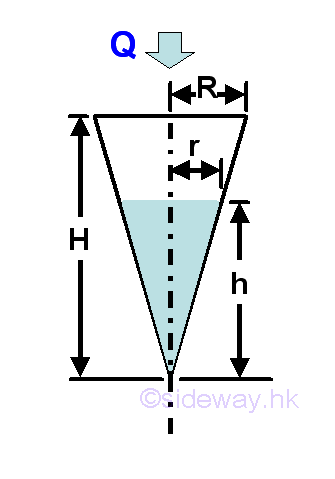
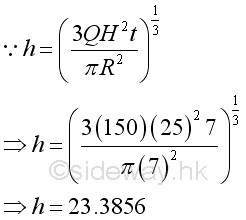 and
and




